关于遍历分解的一个注记

A Remark on Ergodic Decomposition

摘要: 遍历性是遍历论中的基本概念之一，遍历分解定理告诉我们任何一个不变测度都可以表示成一些遍历测度的积分。本文对一类具有遍历根系统的保测变换的遍历分解给出了一个简单的刻画。

Abstract: Ergodicity is a fundamental notion in ergodic theory. The Ergodic Decomposition Theorem indicates that any invariant measures can be represented by the integral of some ergodic components. This paper is concerned with the measure preserving transformation with ergodic root system, and shows that the ergodic decomposition of such a system is simple.

1. 引言

遍历论是动力系统的一个分支，主要从测度的观点研究动力系统的渐近性质。简言之，一个动力系统就是一个二元组 $\left(X,T\right)$ ，其中X 是一个集合，T是X到其自身的一个映射，动力系统理论的主要目标就是描述当n趋于无穷大时 $T^n\left(x\right)$ 的渐近行为。动力系统来源于古典统计力学，此时X表示一个物理对象的所有状态所组成的集合(称之为状态空间或相空间)，T表示这个物理对象所遵守的物理定律。给定一

个初始状态x， $T\left(x\right)$ 表示经过一个单位时间后的状态，则 $\left\{T^n\left(x\right):n\ge 1\right\}$ 就包含了初始状态x随时间演变

的所有信息，从而我们可以用数学工具描述 $T^n\left(x\right)$ 随时间演变的渐近行为。通常我们需要对X和T加上一些条件，从而将动力系统分成以下三个范畴：1) X是一个光滑流形，T是X上的可微映射，这就是微分动力系统；2) X是一个紧度量空间，T是X上的连续映射，这就是拓扑动力系统；3) X是一个概率空间，T是X上的保测映射，这就是遍历论。

给定一个Borel概率空间 $\left(X,\mathfrak{B},\mu \right)$ ，其中 $\mathfrak{B}$ 和 $\mu$ 为X上的Borel -代数和概率测度。我们有：

定义1.1 我们称T为Borel概率空间 $\left(X,\mathfrak{B},\mu \right)$ 上一个保测变换，如果T满足：

1) T是可测的，即 $E\in \mathfrak{B}\Rightarrow T^{-1}E\in \mathfrak{B}$ ；

2) $\mu$ 是T-不变的，即 $\mu \left(T^{-1}E\right)=\mu \left(E\right)$ 对所有 $$ 成立。

此时，我们称 $\left(X,\mathfrak{B},\mu ,T\right)$ 为一个保测变换。

定义1.2 设 $\left(X,\mathfrak{B},\mu ,T\right)$ 为Borel概率空间上的保测变换，如果对所有满足 $T^{-1}E=E$ 的可测集E都有 $$ 或 $\mu \left(X\backslash E\right)=0$ ，则称 $\left(X,\mathfrak{B},\mu ,T\right)$ 为一个遍历保测变换。此时，称 $\mu$ 关于T是遍历的。

遍历性是遍历论中一个基本而重要的概念，与拓扑动力系统中极小性相似，它意味着在某种意义下保测变换是不可分解的。遍历性的概念来源于著名物理学家Boltzmann的“遍历假设”，它断言一个动力系统的观测量的时间平均渐近地等于其空间平均。基于这个思路，Birkhoff [1] 在1931年证明了如下遍历论的基本定理(参见 [2] [3] [4] )：

定理1.1 (Birkhoff点态遍历定理)设 $\left(X,\mathfrak{B},\mu ,T\right)$ 为Borel概率空间上一个保测变换，则对于任意 $f\in L^1\left(X,\mathfrak{B},\mu \right)$ ，存在可积函数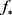使得

其中， $a.e.$ 和 $L^1$ 分别表示几乎处处收敛和 $L^1$ 收敛。特别地，当 $\left(X,\mathfrak{B},\mu ,T\right)$ 为遍历保测变换时，函数 $f_{\ast }$ 几乎处处等于f关于 $\mu$ 的积分。

Birkhoff点态遍历定理为Boltzmann的“遍历假设”提供了一个严格的数学表述，并为动力系统的渐近行为提供了一个定量描述。很多典型的保测变换都是遍历的，比如单位圆环上的无理旋转、有限符号空间上的移位映射、2维环面上的双曲自同构等。一个自然的问题是，非遍历的系统是否可以分解成一些遍历的系统，从而我们可以通过研究这些遍历的系统来研究原来的非遍历系统？下面的遍历分解定理对这个问题提供了一个肯定的回答，关于这个定理的不同表述可参见 [2] [3] [5] 。

定理1.2 (遍历分解)设 $\left(X,\mathfrak{B},\mu ,T\right)$ 是Borel概率空间上一个保测变换， $\Im =\sigma \left(\left\{E:T^{-1}E=E\right\}\right)$ 为X的所有T-不变子集组成的Borel 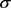-代数。则存在一族关于 $$ 的条件测度 $\left\{{\mu }_x:x\in X\right\}$ 使得

1) 对任何 $f\in L^1\left(X,\mathfrak{B},\mu \right)$ ，有 ${\displaystyle \int f\left(x\right)\text{d}\mu \left(x\right)}={\displaystyle \iint f\left(y\right)\text{d}{\mu }_x\left(y\right)\text{d}\mu \left(x\right)}$ ；

2) 对于几乎所有的 $x\in X$ ， ${\mu }_x$ 是T-不变的且关于T遍历。

定理1.2的表述引自 [4] ，其证明用到了条件测度的存在性。对于紧度量空间上的遍历保测变换，上述定理的证明可参见 [2] [5] [6] 。遍历分解定理告诉我们，任何T-不变测度都可以写成一些关于T遍历的测度的凸组合，从而为研究保测变换 $\left(X,\mathfrak{B},\mu ,T\right)$ ，只需研究其遍历组分。虽然定理1.2告诉我们遍历分解的存在性，却没有提供一个寻找遍历分解的方法。一般地，由于X上所有T-不变测度组成的空间比较复杂，因此寻找一个T-不变测度的遍历分解比较困难。本文中，我们将对一类特殊的保测变换刻画其遍历分解。

2. 定理及证明

定理 2.1 设 $\left(X,\mathfrak{B},\mu ,T\right)$ 为Borel概率空间上一个遍历保测变换，且 $\mu$ 关于T的某个幂 $T^k$ ( $k>1$ )不是遍历的。设 $\nu$ 是 $\mu$ 关于 $T^k$ 的一个遍历组分，则 $\mu$ 关于 $$ 的任何遍历组分都属于集合 $\left\{\nu ,T\nu ,\cdots ,T^k\nu \right\}$ (其中 $T\nu =\nu \circ T^{-1}$ 表示 $\nu$ 关于T的拉回测度)，且 $\mu$ 可以唯一表示成 $$ 的凸组合。

证明：首先考虑 $k=2$ 的情形。由于 $\mu$ 关于 $T^2$ 不是遍历的，则存在Borel集 $B\in \mathfrak{B}$ 满足 $T^{-2}B=B$ 且 $\mu \left(B\right)\in \left(0,1\right)$ 。令 $E=B\cup T^{-1}B$ ， $F=B\cap T^{-1}B$ ，则E和F都是T-不变集，由 $\mu$ 关于T的遍历性得 $\mu \left(E\right)=1$ ， $\mu \left(F\right)=0$ 。故在相差一个零测集的意义下， $X=B\cup T^{-1}B$ ， $\mu \left(B\right)=\mu \left(T^{-1}B\right)=1/2$ 。定义两个概率测度 ${\mu }_1$ 和 ${\mu }_2$ 如下：

${\mu }_1\left(A\right)=2\mu \left(A\cap B\right),{\mu }_2\left(A\right)=2\mu \left(A\cap T^{-1}B\right),\forall A\in \mathfrak{B}.$

易证， ${\mu }_1$ 和 ${\mu }_2$ 都是 $T^2$ -不变的，下面证它们也是关于 $T^2$ 遍历的。事实上，如果存在集合 $A\in \mathfrak{B}$ 使得 $T^{-2}A=A$ 且 ${\mu }_1\left(A\right)\in \left(0,1\right)$ ，则我们有 $0<\mu \left(A\cap B\right)<\mu \left(B\right)=1/2$ 。令 $C=A\cap B$ ，对C进行上述与B一样的推理，可得，这与 $$ 矛盾。故 ${\mu }_1$ 关于 $T^2$ 遍历，用类似的方法可证 ${\mu }_2$ 关于 $T^2$ 遍历。对任意可测集 $A\in \mathfrak{B}$ ，由前面的结果可得：

$\mu \left(A\right)=\mu \left(A\cap B\right)+\mu \left(A\cap T^{-1}B\right)=\frac{1}{2}{\mu }_1\left(A\right)+\frac{1}{2}{\mu }_2\left(A\right),$

故 $\mu =\frac{1}{2}{\mu }_1+\frac{1}{2}{\mu }_2$ ，即 $\mu$ 可被写成两个遍历测度 ${\mu }_1$ 和 $$ 的凸组合。由于 $T^{-2}B=B$ ，故 ${\mu }_1=T{\mu }_2$ 。

当 $k>2$ 时，因为 $\mu$ 关于 $T^k$ 不是遍历的，则存在Borel集 $B\in \mathfrak{B}$ 满足 $T^{-k}B=B$ 且 $\mu \left(B\right)\in \left(0,1\right)$ 。令 $E={\displaystyle {\cup }_{i=0}^{k-1}{T}^{-i}B}$ ， $F={\displaystyle {\cap }_{i=0}^{k-1}{T}^{-i}B}$ ，则E和F都是T-不变集，由遍历性可得 $\mu \left(E\right)=1$ ， $$ 。选取 $0\le l\le k-1$ 以及l个整数 $0\le k_1<k_2<\cdots <k_l\le k-1$ 使得l为满足 $\mu \left(T^{-k_1}B\cap \cdots \cap T^{-k_l}B\right)>0$ 的最大整数，记 $$ 。类似于 $k=2$ 情形，令

$E^{\prime }=B^{\prime }\cup T^{-1}{B}^{\prime }\cup \cdots \cup T^{-\left(k-1\right)}{B}^{\prime },F^{\prime }=B^{\prime }\cap T^{-1}{B}^{\prime }\cap \cdots \cap T^{-\left(k-1\right)}{B}^{\prime }，$

则 $E^{\prime }$ 和 $F^{\prime }$ 都是T-不变集，由遍历性可得 $\mu \left(E^{\prime }\right)=1$ ， $\mu \left(F^{\prime }\right)=0$ 。由 $B^{\prime }$ 的构造，对于 $i\ne j$ ，若 $T^{-i}{B}^{\prime }\ne T^{-j}{B}^{\prime }$ ，则必有 $\mu \left(T^{-i}{B}^{\prime }\cap T^{-j}{B}^{\prime }\right)=0$ ，即在相差一个零测集的意义下， $T^{-i}{B}^{\prime }$ 和 $T^{-j}{B}^{\prime }$ 互不相交。记 $B_1,B_2,\cdots ,B_m\left(m\le l\right)$ 为这样得到的m个互不相交的集合，由于 $\mu$ 是T-不变测度且 $\mu \left({\displaystyle {\cup }_{i=1}^m{B}_i}\right)=1$ ，故这m个集合的测度都是1/m。我们定义m个概率测度如下：

${\mu }_i\left(A\right)=m\mu \left(A\cap B_i\right),\forall A\in \mathfrak{B},i\in \left\{1,2,\cdots ,m\right\}.$

类似于 $k=2$ 情形，可证 ${\mu }_1,{\mu }_2,\cdots ,{\mu }_m$ 关于 $T^k$ 是遍历不变测度，且

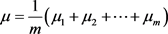
同样地，可证对任意 $1\le i\le m$ 有 ${\mu }_i=T^{i-1}{\mu }_1$ 。

下面证明上述遍历分解是唯一的。由Birkhoff点态遍历定理(定理1.1)，对于任意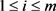和 ${\mu }_i$ -几乎所有的 $x\in B_i$ ，我们有

则从 $L^1\left(X,\mathfrak{B},\mu \right)$ 到 $ℝ$ 的映射 $f\to c_i\left(f\right)$ 定义了一个正线性泛函，由Riesz表示定理(参见 [7] )，这个正线性泛函对应于一个Borel概率测度 ${\mu }_x$ ，使得 ${\displaystyle \int f\left(y\right)\text{d}{\mu }_x\left(y\right)}=c_i\left(f\right)$ 。因此，若 $x,y\in B_i$ ，则相应地可得遍历测度 ${\mu }_x,{\mu }_y$ ，它们相互非奇异，从而 $$ 并且 ${\mu }_x\left(B_i\right)={\mu }_y\left(B_i\right)=1$ ，这说明对于几乎所有的 $x\in B_i$ ，我们有 ${\mu }_x={\mu }_i$ 。故上述遍历分解是唯一的。 $\square$

注记2.1 对于一个保测变换 $\left(X,\mathfrak{B},\mu ,T^{\prime }\right)$ ，如果存在 $\left(X,\mathfrak{B},\mu \right)$ 上的遍历保测变换T使得 $T^{\prime }=T^k$ ，则称T是 $T^{\prime }$ 的一个k次方根，称 $\left(X,\mathfrak{B},\mu ,T\right)$ 为 $\left(X,\mathfrak{B},\mu ,T^{\prime }\right)$ 的一个k次根系统。定理2.1告诉我们如果一个保测变换存在一个遍历的k次根系统，则这个保测变换的遍历组分至多为k个，其遍历分解就是这些遍历组分的凸组合。

基金项目

中国博士后科学基金(2018M643061)。