1. 引言
热带太平洋是全球气候变化的最重要区域之一,其中厄尔尼诺–南方涛动(El Niño-Southern Oscillation,简称ENSO)是其中最强的信号。尽管ENSO事件发生在热带太平洋,但其发生发展会通过大气遥相关等途径影响全球气候变化,引发多种气象灾害,造成重大的经济损失和社会影响。因此,ENSO事件的准确预测也成为各国气象学家密切关注的问题。
目前,ENSO的预报主要分为动力学模型和统计学模型两大类别。动力学模型通过对ENSO相关的物理过程进行建模与数值计算,逐步积分得到预报结果。自20世纪80年代以来,国内外许多机构研制了许多ENSO预报模式 [1] ,已经具备了6~12个月的预报可信度。但动力学模式预报结果仍存在许多不足之处,例如春季预报障碍、误差累积、以及不同模式预报结果存在显著差异等。统计学模型通过挖掘历史数据信息,对其反应的物理规律进行建模并预测。研究表明,利用典型相关分析 [2] 、支持向量机 [3] ,奇异谱分解 [4] 等模型预测ENSO事件,都取得了较好效果。但由于ENSO事件是复杂的非线性物理过程,而许多统计学模型对ENSO非线性作用的建模能力有限。
近年来,随着人工智能技术的飞速发展,深度神经网络模型也被广泛应用各个领域。深度神经网络通过训练出一个庞大的线性与非线性函数的组合,从而可以拟合任意的复杂函数。很多学者也尝试使用深度神经网络进行海洋气象要素或现象预报 [5] [6] [7] ,或者是ENSO事件的预报研究 [8] ,取得了很好的结果。但由于ENSO指数观测数据较短等原因,少有研究仅利用ENSO相关指数的时间序列,通过深度学习方法研究其可预报性。而最近,谷歌提出了一种基于时间序列的长短记忆神经网络模型(Long short-term memory,简称LSTM),可以对较短的时间序列进行建模并预测,在金融等领域上取得了较好的效果。因此,本文将基于时间序列LSTM模型,研究ENSO事件相关指数的可预报性,并探讨造成不同指数间预报能力差异的原因。
2. 模型介绍
深度神经网络(Deep neural network,简称DNN)是一种模仿动物神经网络,进行分布式并行信息处理的算法模型。DNN通常有一个输入层,一个或多个隐藏层及输出层组成,在上层神经元的值通过连接权重加权求和,并通过非线性函数(如Sigmoid函数,Tanh函数,ReLU函数等)激活,然后输入下一层神经元并进行非线性处理作为当前层的输出,重复直到输出最终结果。DNN的参数训练采用了反向传播算法,其过程简单来说,首先随机设置网络参数的初始值,并将当前输出与目标输出之间的差异,定义为损失函数,并通过链式法则,逐层计算损失函数对各层参数的偏导数,并将其乘以学习率加到原始参数上,得到更新后的模型,反复迭代这一过程,直至模型收敛达到稳定。
但对于ENSO等时间序列数据,传统的DNN并不能较好学习数据特征,原因是因为模型无法处理数据之间的时间依赖性。为了利用神经网络处理序列问题,Hopfield等人 [9] 提出了循环神经网络(Recurrent Neural Network,简称RNN),在传统的神经网络中引入环状结构,即在每层神经元彼此之间的序列连接,从而可以将上一时间点的输入以记忆的形式存在网络中,并作为下一个时间点的输入之一。如图1所示,传统深度神经网络仅是将当前层神经元与下一层神经元进行全连接,而没有考虑同一隐藏层内神经元间的时序关系,而RNN通过将同一层内神经元顺序相连,每个神经元同时接受上一层相同时刻与当前层之前时刻的输入,从而达到对数据的时序关系建模的目的。但RNN在网络训练的过程中,采用时间反向传播算法,即在同一隐藏层内,沿时间步进行误差的反向传播与参数更新,但由于误差梯度的反向传播在时间维为累乘,非常容易发生梯度消失或爆炸现象,无法有效更新参数。为了解决这一问题,有学者提出了LSTM单元结构 [10] ,将反向传播过程中梯度由累乘转为累加,从而一定程度上避免了梯度消失或爆炸问题。LSTM模型也是一种RNN结构,每个隐藏层由一连串相同参数的LSTM单元组成,每个LSTM单元将上一个步的输出结果与当前步骤的输入数据一起作为输入,并当前处理结果传递到下一个LSTM单元,如此循环直至最终输出结果。每个LSTM神经元内数据处理过程如公式1所示:
(1)
其中,
、
、
、
、
、
、
、
、
等是权重参数, 每个隐藏层内LSTM单元的这些参数是完全相同,且在训练过程中不断调整。
为sigmoid函数,每个
也可以看作一个“门”,通过非线性变换将数据压缩成0~1之间的概率值,因此也被分别称为输入门(Input Gate),更新门(Update Gate)和输出门(Output Gate)。⊙为两个向量对应元素点乘,
、
和
分别是当前LSTM单元的输入与输出,其中
既可以作为历史信息传递到下一个LSTM单元继续计算,也可以作为模型在当前时刻的输出结果传递到下一层或者计算最终输出。

Figure 1. The schematic diagram of DNN and RNN
图1. DNN与RNN的模型结构示意图
3. 实验过程
3.1. 数据介绍
ENSO是一种发生在热带太平洋的海气相互作用过程,因此有许多定义从不同角度来描述了ENSO事件。在海洋中,最具代表性的描述是Niño 3.4指数,其定义是5˚N~5˚S,170˚W~120˚W区域海表面温度距平场的空间平均。而在大气中,最具有代表性的描述是南方涛动指数(Southern Oscillation index,简称SOI),其定义为达尔文岛和塔希提岛标准化海平面气压异常场的差值(塔希提岛-达尔文岛)。因此,本文采用了由美国国家大气研究中心(National Center for Atmospheric Research,简称NCAR)提供的Niño 3.4指数,作为海洋中ENSO事件的指标,和来自美国海洋与大气中心(National Oceanic and Atmospheric Administration,简称NOAA)提供的SOI指数,作为大气中ENSO事件的衡量指标。两种指数的起止时间均为1951年1月至2018年12月。
为了评价模型预测能力,我们将数据分为两个部分。其中1951年1月至2008年12月,共708个月数据作为训练集,用于模型训练与拟合测试。而2009年1月至2018年12月的十年间的数据作为测试集,用于独立评估模型预测能力,不参与建模过程。图2展示了在两种指数在训练集与测试集中的部分统计特征,可以发现,Niño 3.4和SOI指数在测试集的均值和方差都较训练集有一定的上升,且测试集中二者的最大值(即15/16年超强厄尔尼诺事件)也超过历史训练集,这可能与全球变暖背景下,热带太平洋海温平均气候态上升,ENSO事件强度增强,极端厄尔尼诺事件频率上升有关 [11] [12] 。训练集和测试集间的差异可能会对模型预测能力造成一定的影响。
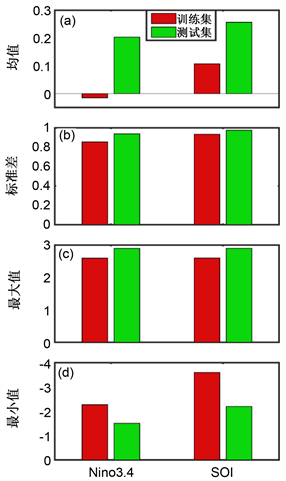
Figure 2. The mean (a), standard deviation (b), maximum (c), minimum (d) in train (red) and test (green) set of Niño 3.4 and SOI index
图2. 在训练集(红色)和测试集(绿色)中,Niño 3.4和SOI指数的均值(a),标准差(b),最大值(c)和最小值(d)
3.2. 模型训练
目前,有许多成熟的开源深度学习框架,可以方便使用者进行深度神经网络的学习与使用,如TensorFlow,Pytorch,Keras等,本文采用了由谷歌开源的TensorFlow Time Series (简称TFTS)进行时间序列LSTM建模。相对于其他深度学习框架,TFTS在时间序列问题上做了专门的优化,如采用时间点+观测值的输入方式,使模型可用于不均匀间隔的时间序列建模或预测,以及使用截断的反向传播算法,使利用小样本进行超长序列的模型训练时也可以有效更新参数等。此外,由于本文中数据量与模型相对较小,因此无需使用GPU进行训练加速。
本文采用了如图1所示的RNN模型结构,其中每个神经元为LSTM单元,其中模型的隐藏层为4层,窗口长度为60。由于是回归类预测任务,模型的目标函数为均方根误差,学习率为1e−3,优化器为Adam。每个模型最大训练2000轮。在预测时,我们将预测起点之前的历史数据输入模型,并从当前时间开始进行预测,并将预测结果作为当前输入,向后逐点预测12个月。此外,由于模型要求时间序列的连续性,模型训练过程中无法进行交叉检验,为了确保预报结果的可靠性,本文通过独立重复5次模型的训练与预测,并对预测结果进行多模型平均作为最终预报结果。
4. 结果分析
图3展示了自2010年1月至2018年12月期间(由于无法对09年数据进行12个月的提前预测,因此09年预报结果统一不参与比较),模型在预测时效为1、3、6和12个月预报时效下的预测结果与实际Niño 3.4指数的比较,图5展示了模型预测结果与实际Niño 3.4指数的相关系数及均方根误差。可以发现,时间序列LSTM模型在1~6个月预报时效下,可以准确预测实际Niño 3.4指数的变化(相关系数超过0.94,均方根误差小于0.2)。在7~12个月预报时效下,尽管模型的预报能力有所降低,但模型仍然可以较好地把握Niño 3.4指数的变化趋势(相关系数超过0.85,均方根误差小于0.45),说明Niño 3.4指数对ENSO事件的物理过程已经有较为完整的反映,具备一定的可预报性。从图3还可以发现,多数时间内,模型在1~12个月预报时效内的预报结果与观测值比较吻合,但对于15/16年间超强厄尔尼诺事件,模型的短期预报结果存在一定的振幅偏差,且预报误差随预报时效的延迟逐步增大,表明模型对于训练数据中并没有发生过极端厄尔尼诺或拉尼娜事件,模型的预测能力仍有一定的不足。
我们比较了时间序列LSTM模型与其他部分统计学预报模型的预报能力。文献 [4] 利用神经网络和谱分解方法进行了Niño 3.4指数的预测,其在3个月和6个月预报时效内的相关系数分别为0.76与0.61;文献 [3] 利用小波分析和最小二乘SVM模型预报了Niño区域温度距平场,其相关系数分别为0.97和0.89;文献 [8] 采用了多变量的Seq2seq2神经网络模型,进行了Niño 3.4指数预测,其相关系数分别为0.81和0.65。而本文的时间序列LSTM模型在3个月和6个月预报时效内的相关系数分别是0.96和0.94,表明时间序列LSTM对Niño 3.4指数的预报有一定的预报能力优势。
本文还研究了时间序列LSTM模型对大气中SOI指数的预报能力。图4展示了相同时间段内,LSTM模型在预测时效为1、3、6和12个月预报时效下的SOI指数预报结果与预报值的比较,图5展示了预报结果与实际SOI指数的相关系数与均方根误差分布。可以发现,在1~3个月短的预报时效下,模型对SOI的变化有一定的预测能力(相关系数大于0.69,均方根小于0.53),对10/11年间的拉尼娜事件和15/16年间的厄尔尼诺事件也有一定的反映能力。然而随着预报时效延长,模型的预报能力快速下降,在12个月预报时效下,尽管模型仍可以一定程度上反映出SOI的变化趋势(相关系数为0.41),然而的预报值普遍较小,与观测的均方根误差达到0.93。从图4的Niño 3.4指数与SOI指数的对比也可以看出,模型对SOI指数的预报能力远低于对Niño 3.4指数的预报能力,因此,也鲜有研究关注SOI指数的可预报性。
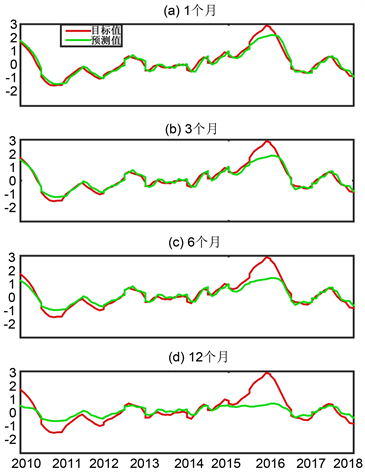
Figure 3. Prediction results and observed Niño 3.4 index
图3. Niño 3.4指数的预报值与观测值
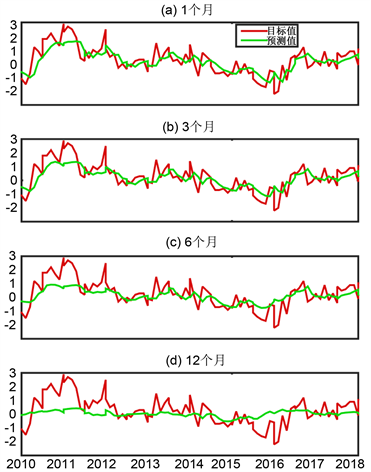
Figure 4. Prediction results and observed SOI index
图4. SOI指数的预报值与观测值

Figure 5. The correlation coefficient and root-mean-square error between prediction results and observed Niño 3.4 index or SOI
图5. Niño 3.4指数(红色)与SOI指数(绿色)的预报值与观测值的相关系数和均方根误差
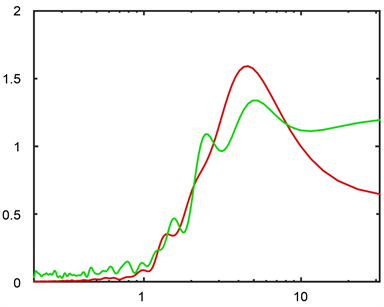
Figure 6. The power spectra density of Niño 3.4 (red) and SOI (green) index
图6. Niño 3.4指数(红色)与SOI指数(绿色)的功率谱密度
为了研究模型对Niño 3.4指数与SOI指数预报能力差异的主要来源,我们利用pwelch方法,对Niño 3.4指数与SOI指数进行了功率谱分析,结果如图6所示。可以发现,尽管Niño 3.4指数与SOI指数在时域上接近,二者间的相关系数达到−0.71。然而二者在频域特征上仍然有显著的差别。Niño 3.4指数在3~6年内有显著的年际准周期的谱峰,这是由于海洋中决定厄尔尼诺现象的赤道开尔文波和罗斯贝波在太平洋海盆完成调整的时间大约是2年 [13] 。而南方涛动作为海洋中厄尔尼诺事件在大气中的响应,SOI的频谱也具有与Niño 3.4指数近似周期的年际准周期谱峰。然而,由于大气比热容较小,海平面气压场的热力学性质除了受下垫面海洋的影响外,受季节尺度的高频变化影响也非常显著,因此SOI在1年以内频段上的功率谱密度显著强于Niño 3.4指数。这种高频的随机噪声严重降低了模型对SOI指数的预报能力。进一步的实验结果也表明,在对SOI指数进行7个月的滑动平均,以去除高频随机信号,时间序列LSTM模型对不同预报时效下,对SOI指数的预报能力有了显著的提升。如图7所示,滑动平均后的SOI至于与Niño 3.4指数相关系数为−0.75,较原始序列有所提高。在1~3个月预报时效内,模型的预报结果与观测较为接近,而在6~12个月内,模型也能较好地反映出SOI指数的变化趋势。此外,模型在3个月和6个月预报时效内,预报结果的相关系数(均方根误差)分别达到了0.96 (0.24)和0.87 (0.40),接近Niño 3.4指数的预报水平。
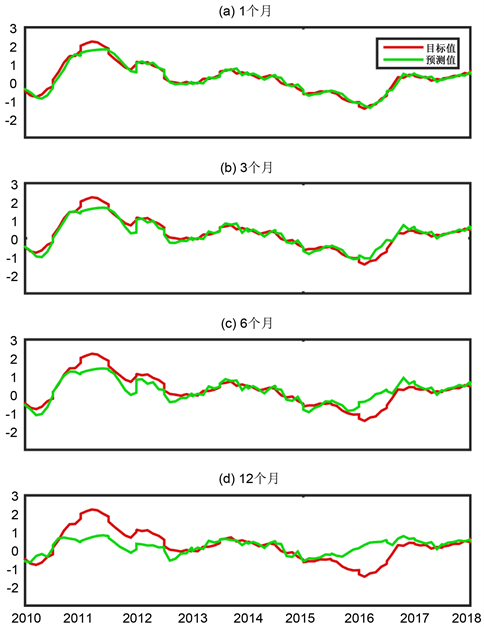
Figure 7. Prediction results and observed 7-months run-mean SOI index
图7. 7个月滑动平均的SOI指数的预报值与观测值
5. 结语
本文基于时间序列LSTM模型,进行了ENSO事件在海洋中的Niño 3.4指数的预报研究。结果表明,尽管对于15/16年超强厄尔尼诺事件的预报上存在一定的偏差,时间序列LSTM模型对Niño 3.4指数在1~12个月预报时效内都有较强的预报能力,与其他统计预报模型的对比结果表明,时间序列LSTM模型预报能力也具有一定的优势。另外,许多统计学模型在预测不同时间段的数据时,往往需要更新数据并重新训练,工作量大。而本文使用的时间序列LSTM模型。仅需要训练一次模型便可进行不同时间内的数据预测。
本文还利用时间序列LSTM模型,研究了ENSO事件在大气中的SOI指数的预报研究,结果表明模型对SOI指数并不具备中长期的可预报性。进一步的研究表明,尽管Niño 3.4指数与SOI指数高度相关,然而SOI指数还受到季节内高频变化的影响,其功率谱分析具有显著的季节内随机噪声特征,这是造成模型对SOI指数预报误差的主要来源。实验结果也证明,模型对7个月滑动平均的SOI指数也有与Niño 3.4指数接近的预报能力。
致谢
感谢中国海洋大学物理海洋实验室陈显尧老师对本文的意见与支持。
基金项目
本文由中央高校基本科研业务费专项(201841014)资助。