1. 引言
众所周知,早在1961年J. G. Ceder就证明了
,同时他提出问题:
和
是否成立? [1] G. Gruenhage和H. J. K. Junnila分别于1976年和1978年独立证明了
空间和
空间是等价的,但
或
是否成立,是至今没有解决的难题 [1]。这里通过对这一问题的研究,利用层对应的方法尝试证明
与
等价的可能性。文中符号:1)
:等价于;2)
:并集;3)
:交集;4)
:E的闭包;5)
:A与B的差集。
2. M1与M3等价的证明过程
2.1. 引入紧缩映射
,
具有如下性质
对于任意拓扑空间S有
(为便利记
),满足
是子空间。那么对任意的拓扑空间A和B有
、
,并且满足以下两种情形:
1) 若
,显然
;
2) 若
,必有
。
同理容易推广到可数个拓扑空间
,无论
是否为
,都有
,这是交集的情况,接下来需要考虑并集的情况。
对任意两个拓扑空间A和B,若
,由于
、
,所以有
,其中
;若
,不妨设
,则可能存在四种关系:
1)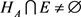 ,
;
,
;
2)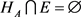 ,
;
,
;
3)
,
;
4)
,
。
然而不论哪种关系,由于
,都可归结为
,其中令
,仍然是
,显然
。同理可容易将
推广到可数个拓扑空间
,即
,因此可以找到
的子空间T使得
成立。
2.2. 紧缩映射的性质的进一步讨论
根据前面的定义,对任意的拓扑空间S, ,其中
是S的子空间,那么对于任意的开集
,由相关定义 [2] ,存在一个基元素
,这里
是
的拓扑的基,满足对于一点
,有
且
。因为
是
的拓扑的基,根据基的定义 [2] ,对每一个
,至少存在一个包含x的基元素B,由
的定义,则
,且
,其中
是S的子空间,那么对于任意的开集
,由相关定义 [2] ,存在一个基元素
,这里
是
的拓扑的基,满足对于一点
,有
且
。因为
是
的拓扑的基,根据基的定义 [2] ,对每一个
,至少存在一个包含x的基元素B,由
的定义,则
,且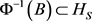 ,所以
,
,因而有
,
。
,所以
,
,因而有
,
。
仍考虑基的定义,若
,则有
使得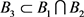 ,这里
。那么由
的定义,因为
,所以知
、
,因而
,
,所以
。因为存在
使
,这里
。那么由
的定义,因为
,所以知
、
,因而
,
,所以
。因为存在
使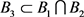 ,所以
,即
,所以
,即 ,而由
、
,显然有
,
,即
。可以考虑利用之前的关系,即
,显然就有关系
。
,而由
、
,显然有
,
,即
。可以考虑利用之前的关系,即
,显然就有关系
。
综上所述,
是S的拓扑的基,所以对于一点
,有
,因为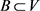 ,所以
,其中已知
是基元素,所以
是开集。所以
是连续的,又因为
是满射,因此
是开映射。同理容易证
将
中的闭集映为S中的闭集,所以
又是闭映射(这与
,所以
,其中已知
是基元素,所以
是开集。所以
是连续的,又因为
是满射,因此
是开映射。同理容易证
将
中的闭集映为S中的闭集,所以
又是闭映射(这与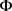 的连续性无关),因此可知
的连续性无关),因此可知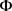 是既开又闭的映射。
是既开又闭的映射。
考虑任意正则空间X,根据相关定义 [2] ,知有任意给定的一点x和不包含x的闭集B,存在开集U和V,使得
,
且
。由
的定义,知
,若任意给定
中的一点y和不包含y的闭集C,使 ,都有
,同样可以找到一个开集
,都有
,同样可以找到一个开集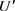 包含y使得
包含y使得 ,所以
也是正则空间。再由Nagata-Smirnov度量化定理 [2] ,将
局部有限基弱化为闭包保持基就得到了
空间,但
空间并不能作为一般的度量空间来考虑,因此不存在与
的拓扑相容的度量d [3] ,因此只能考虑广义度量空间的拓扑结构。由因为
是既开又闭的映射,所以根据相关理论 [1] [4] ,
可能是
空间(这需要在下文进行论证,并且与
,所以
也是正则空间。再由Nagata-Smirnov度量化定理 [2] ,将
局部有限基弱化为闭包保持基就得到了
空间,但
空间并不能作为一般的度量空间来考虑,因此不存在与
的拓扑相容的度量d [3] ,因此只能考虑广义度量空间的拓扑结构。由因为
是既开又闭的映射,所以根据相关理论 [1] [4] ,
可能是
空间(这需要在下文进行论证,并且与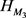 是
空间的论证有关),这一点与将交集关系转化并集关系的思路成为解决后面问题的重要想法。
是
空间的论证有关),这一点与将交集关系转化并集关系的思路成为解决后面问题的重要想法。
3. 层空间对应关系的讨论
3.1. 证明
空间是
空间
在上述定义的映射
的作用下,重点讨论
:
这里取点
,其中 。
。
因此可定义邻域为: ,
其中
,引入空间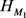 中的基
,且
,这里
中的基
,且
,这里 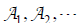 是
的子族。所以就有
是
的子族。所以就有
.
当
时,
显然成立。
则对于
,当
时,就有
。下面考虑一种更复杂的情况:
不妨设
。这里的情况不包含上面的情形,即对于任何
、
有
,或
,则有 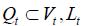 ,其中
。且对于任意的
,其中
。且对于任意的
.
这里若对于集合
,
,考虑
,
,就构成了以下的常规形式,同样地,
,若要满足
需证
,下面分三种情形讨论。
情形1:
,其中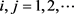
.
因为
,所以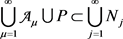 。因为
。因为
,
所以
。所以
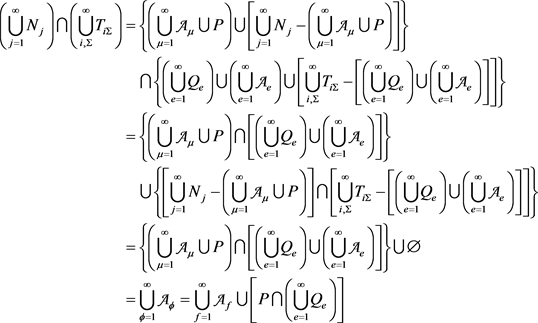 , (1)
, (1)
所以得
,所以当
时可满足条件,或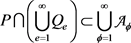 。
。
猜测:是否可能有 ,
?
,
?
若成立则总有
,同样地,也可能出现例如
,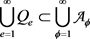 ,如此则总有
。
,如此则总有
。
所以只需
就可成立。
情形2:
当
时,可由(1)式得到
,
所以
,因为
,所以这里可直接令
,即条件可成立。
情形3:
当
时,仍然由(1)式可得:
;
当
时,即
与之前所假设情况的其中之一符合,所以显然成立;当
时,得
也同样如此。因此不论
的情况如何,都有
成立。所以式子
得证。所以经映射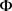 作用后所得到的空间
作用后所得到的空间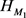 的确是
空间。
的确是
空间。
3.2. 证明
空间是
空间
在映射
的作用下可设
,其中C为闭集,
为开集,所以有
.
由
空间的定义可类似地对
就有,对于另一闭集D,
为开集,所以可设
.
因为
,所以
。因此令
,
当
时,就有
,当
时,
是广义度量空间。
当
时,设 ,所以
,所以当
,所以
,所以当
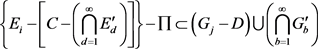
即
时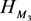 是广义度量空间。
是广义度量空间。
以上证明了
成立的可能性。反过来,若知
,则有两闭集C、D可分别表示为两个开集系列中开集的闭包的交。
设
为闭集,
和
为开集并且
,
.
再设 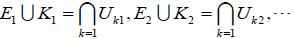 ,
。所以
,
。所以
.
因为已知
,所以可有
其中
,所以
.
根据上面的讨论结果可知:
当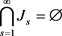 ,
时有
成立。
,
时有
成立。
当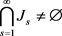 ,
, 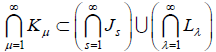 时有
成立。
时有
成立。
因此以上证明了反之条件成立的可能性,所以空间
满足广义度量空间
中的条件,因此
空间的确是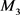 空间。
空间。
3.3. 讨论
的成立性
关于此问题需证明:在
的闭包保持基条件下还可能满足
中的条件,反之,在
的条件下仍有
的闭包保持基条件,两者必须同时成立。
讨论1:
设
, 都是闭集,
为保持基,若
,其中
,
都是闭集,且E满足
都是闭集,
为保持基,若
,其中
,
都是闭集,且E满足 ,令
。因为由保持基的条件就有
,令
。因为由保持基的条件就有
(2)
其中
和
。 (3)
将式(2)和(3)求
就有
因为令
,其中
为开集;和
,
其中
为开集。所以得
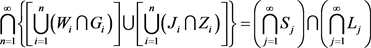 . (4)
. (4)
这里再令
,
,
是闭集,
是开集,其中
,且
所以
。即
是一系列开集
的闭包,代入式(4)得
。因为由
,所以
,所以即有
,
因此以上就证明了任一闭集E可由一系列开集
的闭包的交表示。
当任意两个闭集
有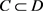 时,若
可易知
;若
时可设
,就有开集
和
时,若
可易知
;若
时可设
,就有开集
和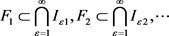 。
。
再设
和
。
因为
且
,所以
。
因此容易得出
其中
,所以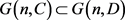 成立。
成立。
讨论2:
设
且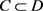 ,
都是闭集,若
,且有一闭集可表示为开集的闭包的交,即有
。当
时,
为
中
的闭包,……,
为
中
的闭包,……。所以
,
都是闭集,若
,且有一闭集可表示为开集的闭包的交,即有
。当
时,
为
中
的闭包,……,
为
中
的闭包,……。所以
 ,
,
所以满足闭包保持基条件。
若
,设
,
是闭集,且有
, 。因为
,所以有
和
所以设
其中
。因为
,所以有
和
所以设
其中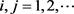 ,同样也有
和
所以
,同样也有
和
所以
所以
.
由此可知,
满足保持基条件,所以
,其中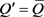 ,
, ,同样满足闭包保持基条件。
,同样满足闭包保持基条件。
4. 总结
以上就证明了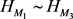 成立的可能性,现在由已知的关于
的定义和正则空间的结构有
成立的可能性,现在由已知的关于
的定义和正则空间的结构有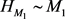 和
~
,很自然就能够得到
和
~
,很自然就能够得到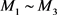 成立,通过与Reznichenko构造反例的结论对比 [5] [6] ,即每个
空间都是
空间。
成立,通过与Reznichenko构造反例的结论对比 [5] [6] ,即每个
空间都是
空间。