1. 引言
在本文中,假设读者熟知Nevanlinna值分布理论的相关基础知识以及常见符号 [1] [2] 。设
是复平面上的亚纯函数,a∈C 为任意的复数,定义a关于f的亏量为
,当
时,a称为f的Nevanlinna亏值。定义
与 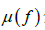 分别为
的级与下级。设a为开平面内的亚纯函数,如果
,则称a为f小函数。设f与g均为非常数亚纯函数,a为f与g的公共小函数,如果
与
的零点相同且每个零点重级也相同,则称f与g CM分担a。如果
与
的零点相同,不考虑零点重级,则称f与g IM分担a。
分别为
的级与下级。设a为开平面内的亚纯函数,如果
,则称a为f小函数。设f与g均为非常数亚纯函数,a为f与g的公共小函数,如果
与
的零点相同且每个零点重级也相同,则称f与g CM分担a。如果
与
的零点相同,不考虑零点重级,则称f与g IM分担a。
设k为正整数。记 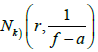 为
的重级
的零点密指量,且计重数。
为
的重级
的零点密指量且计重数。记
为
的零点精简密指量,且不计重数。
为
的零点精简密指量,且不计重数。
为
的重级
的零点密指量,且计重数。
为
的重级
的零点密指量且计重数。记
为
的零点精简密指量,且不计重数。
为
的零点精简密指量,且不计重数。
设F与G均为非常数亚纯函数,且F与G IM分担1。设
为F的一个重级为p的1值点,同时为G的一个重级为q的1值点。记
为F的那些重级
的1值点;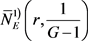 为F的那些重级
的1值点;记
为F的那些重级
的1值点。以上所定义的计数函数每一点只计一次。同样可以定义
,
,
。若F与G IM分担1,则
为F的那些重级
的1值点;记
为F的那些重级
的1值点。以上所定义的计数函数每一点只计一次。同样可以定义
,
,
。若F与G IM分担1,则
设f为非常数有穷正级为
的亚纯函数,
为f的一个小函数。若
,则称
为f的一个Borel例外函数。当 时,定义
的零点个数为有穷个。
时,定义
的零点个数为有穷个。
另外,我们需要定义一些差分算子的符号。设f为非常数亚纯函数,
为f的小函数,
为判别的有穷复数。令
为f的差分多项式。最近,许多人做了关于复差分唯一性的问题。2018年,Huang-Zhang [3] 证明了:
定理A 设
为开平面上的有穷级的超越整函数,
为f的一个Borel例外值, c∈C 为非零有穷复数。设
为
的一个小函数,若
与
CM分担
,则
。
定理B 设
开平面有穷级的超越整函数,
为有穷复数。设
为
的一个小函数,若
与
CM分担
且
,则
。
定理C 设
为开平面有穷级的超越整函数,
为有穷复数。设
为
的一个小函数。若
与
CM分担
且
,则
。
本文推广并改进上述结果,证明了:
定理1 设
为开平面有穷级的超越整函数,
为f的一个Borel例外整函数,
为f的差分多项式,其中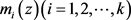 为f的整小函数,
为f的整小函数,  k个判别的有穷复数。
k个判别的有穷复数。
又设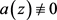 为
的一个整小函数,若
与
IM分担
,则
。
为
的一个整小函数,若
与
IM分担
,则
。
定理2 设
为开平面有穷级的超越整函数,
为f的差分多项式,其中 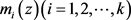 为f的整小函数 ,
为f的整小函数 ,  为任意有穷复数。又 设
为
与
的一个公共小函数,若
与
CM分担
为任意有穷复数。又 设
为
与
的一个公共小函数,若
与
CM分担 且
且 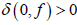 ,则
。
,则
。
2. 几个引理
引理1 [4] [5] [6] 设f为非常数有穷级亚纯函数, c∈C 为非零有穷复数。则
,
其中
,除去r的一个集合E,且集合E的对数测度为有穷的。
引理2 [1] [2] 设f为非常数亚纯函数,则
.
引理3 [7] 设
,其中F与G为两个非常数亚纯函数。若F与G IM分担1且
,则
.
引理4 [2] 设f与g均为非常数亚纯函数,
分别为f与g的级。则
.
引理5 [2] 设f与g均为非常数亚纯函数,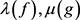 分别为f的级与g的下级。若
,则
分别为f的级与g的下级。若
,则
.
引理6 设f为非常数有穷级整函数。若
为f的一个Borel例外整函数,则
。
证 我们分为以下两种情形讨论:
情形1
。设 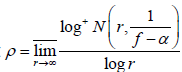 。因
。因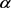 为f的一个Borel例外整函数且f为有穷级整函数,则有
。设
为f的一个Borel例外整函数且f为有穷级整函数,则有
。设 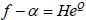 ,其中H为
的零点构成的典范乘积,以及Q为一非零多项式。由
,其中H为
的零点构成的典范乘积,以及Q为一非零多项式。由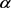 为f的整小函数,从而有
为f的整小函数,从而有 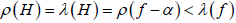 。显然有
,这可推出
。由引理4以及
为正规增长函数,我们可以得到
。显然有
,这可推出
。由引理4以及
为正规增长函数,我们可以得到
,
以及
,
即
。又由引理5可得 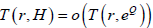 。因此
。因此
,
反过来也可得到
。这可推出
。故我们有
.
情形2
。由我们引言中所定义的
时
的零点个数为有穷个,直接可得
,于是有 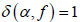 。证毕。
。证毕。
3. 定理1的证明
设
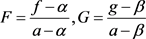 , (1)
, (1)
其中
。因为f与g IM分担a,a为整小函数。所以F与G IM分担1。由(1)有
。因为
为f的整Borel例外函数,则由引理6可以得到
。由引理1可以得到
,
即
。故
。从而有
与
。
定义H为引理3中的函数。假设
,由引理3有
, (2)
其中
为
的零点计数函数,而不是F与
的零点计数函数。同样
也可类似定义。由Nevanlinna第二基本定理可得
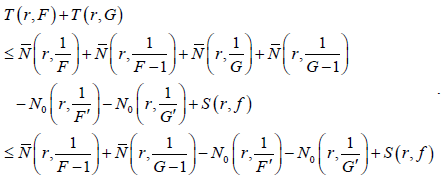 . (3)
. (3)
因为F与G IM分担1,所以我们有
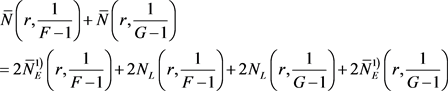 . (4)
. (4)
结合(2)与引理3可得
. (5)
容易发现
. (6)
由(5)与(6)得
. (7)
把(7)代入(3)可以得到
. (8)
由引理2又有
. (9)
由(8)与(9)可得 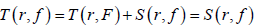 。矛盾。
。矛盾。
因此
。由引理3以及两边积分可得到
, (10)
其中 为常数。从(10)式又可以得到
为常数。从(10)式又可以得到
. (11)
我们分为以下三种情况讨论。
情形1
。由(11)可以得
。由Nevanlinna第二基本定理有
, (12)
即
。矛盾。
情形2 B = 0 。由(11)有
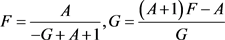 . (13)
. (13)
若
,从(13)可得
。类似于情形1的证明过程我们同样可得矛盾。因此 A=1 。由(10)可知
,即
。
情形3
。由(11)有
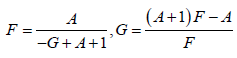 . (14)
. (14)
若
,从(14)可得
,即
. (15)
由(15)得到
. (16)
即
。矛盾。因此定理1得证。
4. 定理2的证明
假设
。因为f与g CM分担a,则
, (17)
其中H为非零多项式。从(17)可得
,
即
. (18)
根据上式可得到
,
即 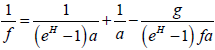 。
。
因此有
. (19)
另一方面,由Nevanlinna第二基本定理
,
于是有
。
因此我们有
。结合(19)立刻有
,即
,这与
矛盾。因此
,其中C为非零常数。若
,则有
,这与设矛盾。故
,从(17)得
。把上式代入(18),且由(19)可得
。即
,这与
矛盾。因此
。定理2得证。
基金项目
国家自然科学基金(NO.11701188)资助。