1. 引言
早在1948年,F. John证明了n维欧氏空间
中的每一个凸体都包含一个唯一的体积最大的椭球,现在我们把这个椭球称为该凸体的John椭球,当这个John椭球是欧氏单位球B的时候,F. John给出了一组充分必要条件,从而把这个单位球刻画了出来。这就是下面著名的John定理(参见 [1] - [6] )。
定理A:n-维欧氏空间
中的每一个凸体K都包含一个唯一的体积最大的椭球。这个椭球是球当且仅当
并且对于某个正整数
,存在一列正实数
,同时在K的边界上存在一列单位向量
满足:
,(1.1)
和
, (1.2)
这里,算子
定义为对于任意
,
,而
表示
上的单位算子。
条件(1.1)表明
类似
中的一组正交基,它的一种等价表示是,对于任意的
,都有下面的等式成立:
, (1.3)
或者
, (1.4)
其中,
表示欧氏空间
中通常的内积。关于上述等价关系的详细论述可参考K. Ball的文章 [2] 。
我们把凸体K的边界上满足(1.1)和(1.2)的点称为接触点。
中最简单的凸体就是立方体
,显然它的接触点就是
中的标准基向量
以及
。
本文的主要目的是利用John定理对2维欧氏平面
中三角形的一些性质做些描述,并得到如下两个结论。
定理1:正三角形的John椭圆就是它的内切圆。
定理2:任意一个三角形的John椭圆是圆当且仅当该三角形是正三角形。
2. 准备知识
在定理的证明中,我们需要用到重心坐标的概念。众所周知,重心坐标是距离几何中的一个常用概念,在三角形中它的定义如下(见 [5] [7] ):
设A是2维欧氏平面
中以
为顶点的一个三角形,且M是
中任意一点,记以
,
和
为顶点的三角形的面积分别为 和
,则我们称面积比
和
,则我们称面积比
为点M关于三角形A的重心坐标,记为
。
从上述定义可知,对于某个点M的重心坐标可记为
,也可记为
,即其记法并非唯一,是可以相差一个非零的常数因子k的。
对于M点的重心坐标
,若令
,则
,则我们称
为点M的规范重心坐标,这就是有限元法中的面积坐标。
假设
是某一个正三角形的顶点,且标准单位圆B是它的内切圆,我们记B与顶点
所对的边
和
上的切点分别为
和
,边
和
上过点
和
的单位外法向量分别为
。根据重心坐标定义,通过简单的计算可得
和
的重心坐标分别为:
。
因此,对任意一个正三角形,它的接触点的重心坐标具有如下的形式:
, (2.1)
其中矩阵的每一行向量代表一个接触点的重心坐标。
3. 定理1的证明
根据John定理,我们只要证明正三角形的内切圆的切点满足John定理即可。首先约定2维欧氏平面
中的正三角形及相关元素的记号同第2节。在此规定下,由重心坐标的定义不难求得坐标原点的重心坐标为
。令
,则
。
于是,我们验证了John定理中的(1.2)式。
下面我们将验证向量
满足John定理中的(1,1)式。事实上我们只需证明与(1.1)式等价的式子如下,即对任意
,都有下面的等式成立:
, (3.1)
其中,
。
由于我们所考虑的凸体是
中三角形
,所以它的3个边
,
和
上的单位法向量
所形成的空间必为
,也即
。
因此,对任意的向量
,一定存在实数
,使得
。
分别以
与上式的两端作内积,我们可得
若记
,
,且向量
的Gram矩阵为
。
因此,上面的方程可改写为
, (3.2)
其中
,
分别表示
和
的转置。
考虑到G的任一元素
是三角形的两个边
与
对应的单位外法向量
与
的夹角的余弦,又由于法向量
与
的夹角与三角形的边
,
所形成的夹角
是互补的,所以
。
我们仍然用
分别表示三角形的边
的边长。对于
,我们有
,
其中
表示边
沿
方向向边
作垂直投影所得到的投影的长度。
为了得到Gram矩阵G的值,我们只需计算
的值即可。由于我们所考虑的是正三角形,所以对于 i ≠ j 所有的
,对于
所有的
。这样就得到了矩阵G,即
。
由此,把(1.2)和(3.2)式联立可得
将
代入上面的方程组可知
是该方程组的一组解。因此
中的任意一点可以表示成(3.1)式的形式,定理1证毕。
4. 定理2的证明
首先,我们介绍H. J. Brascamp和E. H. Lieb 建立的一个著名不等式作为引理(参见 [3] [4] ),它可以被看作卷积不等式的推广,被称为Brascamp-Lieb不等式。
引理4.1:设
是
中的一列单位向量,
是一列正实数,使得它们满足下面的等式:
。
如果
是一列可积函数,那么
。(4.1)
F. Barthe在文 [3] 中给出了引理4.1等式成立的一组必要条件,即下面的引理。
引理4.2:设
是
中的一列单位向量,
是一列正实数,使得它们满足下面的等式:
。
如果
是
中不全为零的函数,并且
不都是高斯分布的密度函数,那么(4.1)式取等式的必要条件是
,
并且
是
的一组正交基。
现在我们给出定理2的证明。
由定理1立即可得定理2的充分性。下面我们证明定理2的必要性,即如果三角形A的John椭圆是欧氏单位圆B,那么三角形A是正三角形。
首先我们注意到如果三角形A的John椭圆是单位圆B,那么这个圆一定是该三角形的内切圆。如若不然,那么不妨设B与三角形的某个边
不相切,设边
的外法向量是
,那么一定存在一个正实数
,使得单位圆B沿方向
平行移动
后,单位圆B不在与三角形A的任何边相切。这时一定存在另一个正实数
,如果我们对单位圆B沿方向
平行移动
后,再令单位圆B做一个膨胀r,使得膨胀后得到的圆rB成为三角形P的内切圆。这与我们的条件——单位圆B是John椭圆相矛盾。
因为三角形A的内切圆是其John椭圆,由John定理,存在一组正实数
以及在A的边界上存在一组单位向量
,使得
, (4.2)
和
。 (4.3)
设
,则K也是
中的三角形。由于
是A和B的接触点,所以
。
注意到B也是三角形A的内切圆且K,A与B有相同的切点
,所以我们有
。
现在问题转化为只需要证明K是正三角形即可。在下面的讨论中,我们把
视为
,令
。
。
容易验证
是单位向量,并且结合(4.2)和(4.3),我们有
。
定义函数列
如下:
对于任意的
,令
,
由引理4.1,我们得到
。 (4.4)
现在,假设
,对于每一个i,我们有
。
因为
,则存在j (仅依赖于y)使得
。因此,如果
,则
。另一方面,如果
,则对于每一个i,当
时,
。从而我们可得
因此对于每一个
,我们可得F在平面
上的积分为:
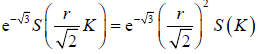 ,
,
其中
表示三角形K的面积。因此由(4.4)式可得
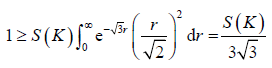 ,
,
即
。 (4.5)
注意到(4.5)式的右端正是以单位圆B为内切圆的正三角形的面积。
考虑到函数
的构造,并对(4.4)式应用引理4.2,可得(4.4)式等式成立的条件是
是
的一组正交基。任取这组正交基中的两个向量
和
,
我们有
,
所以
是一个常数。由于
是三角形
的三个边上的单位外法向量,因此,
是正三角形。定理2证毕。
基金项目
国家自然科学基金资助项目(No: 11561020)。