1. 引言
海洋作为战略性的资源基地,其中蕴含着极其丰富的资源,然而这些资源的探测、开采和运输都要用到海洋平台以及各类船舶。要使这些海洋结构物安全地生产,必须要有可靠的系泊系统来为它们定位,这就促使系泊动力分析成为一项重要的技术领域( [1] [2] [3] [4] [5] )。本文分析船舶在系泊系统作用下的动力特征,再据此讨论系泊系统的参数设计。
近浅海观测网的传输节点由浮标系统、系泊系统和水声通讯系统组成( [6] [7] ),如图1。

Figure 1. Schematic diagram of the transmission node
图1. 传输节点示意图
浮标系统可简化为圆柱体(本文假设底面直径2 m、高2 m,浮标的质量为1000 kg)系泊系统由钢管、钢桶、重物球、电焊锚链和特制的抗拖移锚组成(本文假设锚的质量为600 kg,锚链选用II型无档普通链环,钢管共4节,每节长度1 m,直径为50 mm,每节钢管的质量为10 kg)。要求锚链末端与锚的链接处的切线方向与海床的夹角不超过固定度数,否则锚会被拖行,致使节点移位丢失(见文献 [8] [9] [10] [11] )。本文假设固定度数为16˚,水声通讯系统安装在一个长1 m、外径30 cm的密封圆柱形钢桶内,设备和钢桶总质量为100 kg。钢桶的倾斜角度(钢桶与竖直线的夹角)超过5˚时,设备的工作效果较差。
问题:某型传输节点每节链环长度:105 mm,单位长度质量:7 kg/m,锚链总长:22.05 m,重物球质量:1200 kg。将该型传输节点放在水深18 m、海床平坦、海水密度为1.025 × 103 kg/m3的海域。若海水静止,海面风速为36 m/s,求钢桶和各节钢管的倾斜角度,锚链形状,浮标的吃水深度和游动区域。若要求钢桶的倾斜角度不超过5˚,锚链在锚点与海床的夹角不超过16˚,如何调节重物球的质量?
2. 传输节点受力分析
假设锚链、钢桶、钢管都由刚性物质组成,不会被压缩或拉伸。海面为平面且风力与水流力的方向都平行于海面。
2.1. 传输节点的整体水平受力分析如图2

Figure 2. Schematic diagram of the overall force of the transmission node
图2. 传输节点整体受力示意图
浮标所受的近海风荷载F与锚链所受的水平分力
为一对平衡力,即:
(1-1)
近海风荷载可通过近似公式计算为:
(单位:牛) (1-2)
其中,S表示浮标在风向量的平面投影面积,单位m2;v表示风速,单位(m/s)。又因为浮标受到重力和钢管拉力的作用,会有一部分浸没在水中,所以浮标在风向量的平面投影面积S:
(1-3)
其中,D表示圆柱体浮标的底面直径;H表示圆柱体浮标的高度;h表示浮标沉浸在水中的深度,即浮标的吃水深度。
将式(1-3)带入式(1-2)中,求解得到近海风荷载F的表达式为:
(1-4)
2.2. 单位悬链线静力矩分析及静力分析
以每一小节悬链线的几何中心为力矩中心,由于悬链线处于稳定状态,则各个力的力矩之和必定为零。受力分析如图3:从而可以从
两个方向建立力矩平衡关系式:
(1-5)
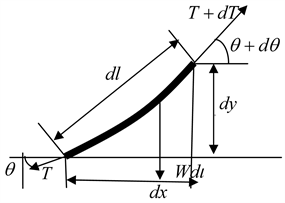
Figure 3. Static diagram of the unit catenary
图3. 单位悬链线的静力图
其中,W表示单位悬链线的重量;
表示单位悬链线的长度;T表示单位悬链的张力;
表示增加一小段
后增加的张力;
表示张力T与水平方向的夹角;
表示增加一小段
后增加的角度。
建立单位悬链线在水平方向和竖直方向上的长度方程:
(1-6)
建立单位悬链线在水平方向和竖直方向上的力平衡方程 [1] :
(1-7)
(1-8)
2.3. 完整悬链线静力分析与静力矩分析
参考文献 [12] ,对完整的悬链线进行受力分析,得到力矩平衡方程和力平衡方程。根据受力分析可以绘制出完整悬链线的静力图,并建立直角坐标系,如图4所示:

Figure 4. Static diagram of the entire catenary
图4. 整条悬链线的静力图
结合完整悬链线的受力分析和
、
、
三个力的平衡条件以及静力矩,可以得到张力
,
与水平分力
的关系式和力矩关系式:
(1-9)
其中,
表示锚对锚链的张力;
表示锚链对铁桶的张力;
分别表示锚对悬链在水平与竖直方向的分力和钢桶对悬链在水平与竖直方向的分力;
和
表示
和
与水平方向的夹角;
表示锚链的张力沿水平方向的分力;
分别表示锚对悬链在水平与竖直方向的径向矢量和钢桶对悬链在水平与竖直方向的径向矢量;锚链的总长度
米。
对式(1-6)~式(1-9)联立求解,计算出整条悬链线的参数方程:
(1-10)
(1-11)
其中,x表示悬链线由a到b的水平距离,y表示悬链线由a到b的竖直距离。
2.4. 悬链线方程求解
令
,
。将
,
带入式(1-10)和式(1-11)中化简得到:
(1-12)
(1-13)
再对式(1-12)进行变形,得到
关于x的关系式为:
(1-14)
将式(1-14)带入式(1-13)进行化简,求解出悬链线方程为:
(1-15)
2.5. 悬链线水平长度随浮标吃水深度变化规律
在悬链线上取单位长度的曲线,这段曲线可视为线段,满足
。利用曲线积分的思想将完整的悬链线分成数量无穷大,长度无穷小的线段。利用勾股定律
求得每一段线段的长度,在将所有的线段长度依次相加得到悬链线的总长度。
在图2所示的直角坐标系中,悬链方程
在
区间中的长度为:
(1-16)
悬链线方程
对x进行求导,得到
的表达式为:
(1-17)
代入式(1-17),得到悬链线长度的表达式为:
(1-18)
将式(1-4)带入式(1-18)整理得到悬链线长度方程:
(1-19)
3. 钢桶受力分析
3.1. 钢桶静力矩分析
由于钢桶在力的作用下是静止作用,因此钢桶的静力矩和为零,因此可以建立静力矩方程式:
(2-1)
3.2. 钢桶受力分析
在悬链线受力不变的情况下,对钢桶进行受力分析,分别建立钢桶关于水平方向,竖直方向和力矩的平衡方程式。根据受力分析,可以绘制出钢桶的静力图如图5所示:

Figure 5. Static analysis of steel drum
图5. 钢桶的静力分析
首先根据钢桶的静力分析,建立钢桶沿水平方向和竖直方向的力平衡方程:
(2-2)
其中,
表示钢管1对钢桶的拉力;
表示钢管1倾斜的角度; 表示锚链对钢桶的拉力,
与式(3-9)中的
为一对相互作用力;
表示
与竖直方向的夹角;
表示钢桶的重力;
表示钢桶的浮力;
表示选用重物球的重力。由于钢桶不转动,则有:
表示锚链对钢桶的拉力,
与式(3-9)中的
为一对相互作用力;
表示
与竖直方向的夹角;
表示钢桶的重力;
表示钢桶的浮力;
表示选用重物球的重力。由于钢桶不转动,则有:
(2-3)
其中,
表示钢桶倾斜的角度;l表示钢桶的长度。求解得到:
,
。又因为钢桶的力矩保持平衡,可列出方程:
(2-4)
其中,
和
分别表示
沿水平方向和竖直方向的分力;
表示钢桶的倾斜角度;将式(2-2)求解出的结果带入式(2-3)得到:
(2-5)
将式(2-2)带入式(2-5)中,消去拉力
,在式两边同时除以
,通过化简得到:
(2-6)
3.3. 钢管静力矩分析
由于钢管在力的作用下是静止作用,因此钢管的静力矩和为零,因此可以建立静力矩方程式:
(2-7)
3.4. 钢管受力分析
在钢桶受力不变的情况下,对钢管1~钢管4进行受力分析,分别建立钢管1~钢管4关于水平方向,竖直方向的力平衡方程。根据受力分析,可以绘制出钢管1~钢管4的静力图如图6:

Figure 6. Static analysis of steel pipe 1
图6. 钢管1的静力分析
首先根据钢管1的静力分析,建立钢管1沿水平方向和竖直方向的力平衡方程:
(2-8)
其中,
表示钢管2对钢管1的拉力;
表示钢管2的倾斜角度;
表示钢管1的重力;
表示钢管1所受的浮力。对式(2-8)进行平方后相加,得到方程:
(2-9)
再同理对钢管2~钢管4进行静力分析,整理后得到方程:
(2-10)
其中,
表示钢管1~钢管4的重力;
表示钢管1~钢管4所受的浮力;
表示锚链对钢桶的拉力。
4. 浮标受力分析
4.1. 浮标静力矩分析
建立静力矩方程式:
(3-1)
4.2. 浮标受力分析
考虑浮标在风向量法平面的投影面积,由图7得到浮标受近海风荷载的影响公式为:
(3-2)
其中D表示浮标底面直径;H表示浮标的高度;h表示浮标吃水的深度;v表示海面风速。
在钢管4受力不变的情况下,对浮标4进行静力分析,绘制出浮标的静力图(如图8)。分别建立浮标关于水平方向和竖直方向的力平衡方程:

Figure 7. Schematic diagram of the buoy on the projection plane
图7. 浮标在投影平面的示意图
(3-3)
5. 系泊系统整体分析
5.1. 系泊系统受力分析
对系泊系统整体进行受力分析,由作用力等于反作用力的条件:
(4-1)
5.2. 系泊系统竖直长度分析
系泊系统竖直长度Y为海平面到海床平面的距离,由锚链竖直方向的长度、钢桶竖直方向的长度、钢管1~钢管竖直方向的长度、浮标的吃水深度组成。即:
(4-2)
5.3. 浮标游动区域的确定
浮标游动的区域由锚链水平方向的长度、钢桶水平方向的长度、钢管1~钢管4水平方向的长度6部分组成,即:
(4-3)
其中,L表示系泊系统水平长度;S表示浮标游动的区域面积;
6. 模型求解
[13] [14] [15]
step1:将锚链左下端切线与海床的夹角
和锚链水平长度
带入(1-17),计算出锚链对钢桶张力的方向与水平线的夹角
step2:由图4可知
与
互余,求得
;根据(1-6)可以求得
。因为
与
为一对相互作用力,可计算出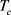 的值。
的值。
step3:将
和
带入(2-5),(2-12),分别计算出钢桶倾斜角度
和
。
step4:将
,
和
带入式(3-3),计算出钢管1的倾斜角度
,钢管2的倾斜角度
,钢管3的倾斜角度
,钢管4的倾斜角度
,锚链张力沿水平方向分力
。
step5:将
和
带入(1-11),求得悬链线方程;利用Matlab做出锚链的形状图。
step6:将锚链水向长度
,钢管1~钢管4的倾斜角
~
带入(4-3),求解出系泊系统水平长度L,浮标游动的区域面积S。即系泊系统浮标的游动区域是以锚为原点,半径为L的圆,浮标游动区域面积为S。
通过Matlab (R2010a)编程实现上诉步骤,计算出系泊系统各个参数的值和锚链方程,画出锚链图像,并最终确定浮标的游动区域。
将重物球质量
,海面风速
带入问题建立的模型进行求解结果如表1所示:

Table 1. Tilt angle of steel drum and each section of steel pipe when sea surface wind speed is 36 (unit: ˚C), buoy draft depth (unit: m)
表1. 海面风速为36 m/s时钢桶和各节钢管的倾斜角度(单位:度)、浮标吃水深度(单位:米)
通过Matlab (R2010a)软件编程得到锚链形状图像如图9:
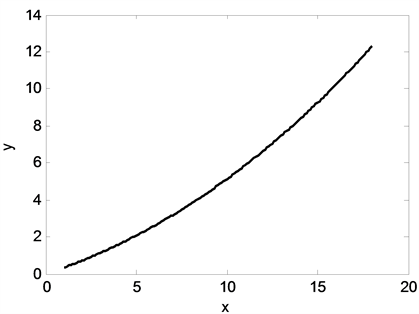
Figure 9. Anchor chain shape when the sea surface wind speed is 36
图9. 海面风速为36 m/s时的锚链形状
锚链方程为:
(5-1)
浮标的游动区域是以锚为原点,半径为18.6721米,游动区域面积为1095 m2。当海面风速为36 m/s时,锚链末端与锚的链的接处的切线与海床的夹角
度。
,锚会被拖行。
列出与重物球相关的方程组
(5-2)
通过联立求解,得到关于重物球重量的方程:
(5-3)
根据重物球重量调节模型,利用Matlab编程求解得到:锚链末端与锚的链接处的切线方向与海床夹角
在一定范围内,随着重物球的重量增加而减小;钢桶的倾斜角
在一定范围内,随着重物球的重量增加而减小。如图10所示
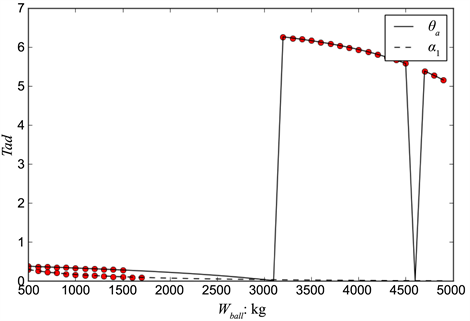
Figure 10.
and
the variation of the weight of the weight ball
图10.
和
随重物球重量
的变化示意图
红色圆点表示不符合题目要求的角度,黑色圆点表示符合。由图9可知,当海面风速为36 m/s时,重物球质量在1700 kg~3200 kg可满使得钢桶倾斜角度不超过5˚;锚链末端与锚的链接处的切线方向与海床夹角
小于16˚。
7. 结果分析
通过海域深度H,海水速度u,风速度V对锚链形状影响探讨,可知随着海域深度的增加,水流速度与风速度固定时,锚链中部略微下垂,但影响不大;随着u增加,在H与V固定的情况下,锚链左端与水平相切角在增大,锚链的曲率半径在减小;随着V的增加,在H与水流速度固定的情况下,锚链左端与水平切向角由负角慢慢变为正角,说明在此深度与水速下,锚链存在一定拖尾现象,随着V的增加,拖尾现象消失,锚链的曲率半径随着水速的增大而增大。
下面检验锚链末端与锚的连接处的切线方向与海床夹角
,铁桶倾斜角
随着重物球质量的变化规律。
从图11分析可知,锚链在锚点与海床的夹角
随着重物球的质量增加而缓慢地增加,说明锚链所受的张力在逐渐增大,且满足夹角
;在500 kg~1700 kg的范围内,铁桶倾斜角度
随着重物球的质量增加而逐渐减小,且满足倾斜角度
,说明重物球的质量增加可以使得铁桶中水声通讯设备的工作效果较好。通过对铁桶、重物球和锚链所构成的系统受力分析,以上分析符合系统力学平衡变化(参见文献 [13] [14] [15] )。
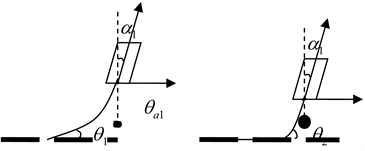
Figure 11. Schematic diagram of the catenary of different weight balls
图11. 不同重物球的悬链示意图
本文模型的优点在于:1) 在求解问题的过程中,采用了逐层分析思想,依次对锚链、钢桶、钢管、浮标进行受力分析,思路清晰,环环相扣,具有很好的可读性。2) 本文运用较多的受力分析图,可以形象直观地反映出物体在水平和竖直方向上的受力关系,解题思路清晰明了。3) 通过单因素控制变量法,简化模型但又不失去本质,较好地解决本题。缺点在于:1) 在考虑海面风对浮标的影响时,忽略了风力在竖直方向的作用;2) 在海水静止时,忽略了海水阻力对浮标的影响。此外,在对基本模型的推导过程中,忽略了水的阻力对浮标的作用。当海面风作用于浮标时,会产生一个水平方向的力F,与海水对浮标的阻力f为一对力偶。当风速v较大时,水平分力F和阻力f会使浮标的重心发生偏移。结合风速,可以大致判断出求解得到的钢桶和各节钢管的倾斜角度比实际值要小,但因为浮标的重力较大,重心偏移的角度非常微小,误差可以忽略不计。
基金项目
四川省大学生创新创业训练计划项目(201710622060, 201810622025)。
NOTES
*通讯作者。