1. 引言
神朔铁路承担着我国西煤东运的任务,线路自然环境恶劣,地形地貌复杂,而且小半径曲线众多。近年来,随着列车轴重的增大以及行车密度的提高 [1] ,钢轨结构的损伤程度进一步加深,尤其是钢轨波磨问题变得日益严重,特别是在小半径曲线地段,钢轨波磨不仅出现早,而且发展快。此外,由波磨引起的钢轨磨耗、联接零件断裂失效、道床翻白等病害也急剧增加,从而导致打磨次数、更换钢轨量、更换失效零配件量都逐渐增大,这些不仅增加了铁路相关部门的养护维修工作量,也严重影响了铁路的经济效益和运营安全。因此,为确保铁路的安全运营、延长钢轨使用寿命、减小轨道养护维修,开展神朔重载铁路小半径曲线地段钢轨波磨方面的研究分析就变得非常必要。
由于钢轨波磨产生机理的复杂性,多年以来行业内也没有形成统一的波磨分类标准。其中最具有代表性的是Zarembski和Grassie综合考虑固定波长机理和损伤机理 [2] 提出的六种类型的波磨分类方法,其具体内容如表1所示,他们认为各类型波磨形成机理不同,应分别予以研究。

Table 1. Rail corrugation classification
表1. 钢轨波磨分类
重载铁路钢轨波磨作为一种长时间存在的病害,始终困扰着铁路相关部门。基于上述研究现状,本文将主要采用SIMPACK多体动力学软件建立C80运煤敞车的精细化模型,对重载铁路小半径曲线地段钢轨波磨的产生原因和影响因素进行数值分析,为明确神朔重载铁路波磨产生机理及提出整治措施提供理论依据。
2. 重载货物列车-轨道耦合模型的建立
重载货物列车是一个复杂的多自由度系统,由很多功能各异的部件组成,这些部件在实际运动过程中会发生复杂的相对运动 [3] 。而且货车为非刚体结构,车体与钢轨,钢轨与轨下结构都存在着复杂的弹性变形,仿真起来有一定的困难。因此在进行动力学研究时,最好根据实际研究的重点和要求,合理地组织安排各部件和因素的主次顺序,并将一些对研究结果影响较小的次要因素进行简化,同时在对动力学性能影响较大的主要因素上做出较为详尽的说明和体现 [4] ,合理处理各部件的相对运动关系,建立好各部件的铰接与约束,将实际系统抽象为力学模型,再根据此建立的系统运动的微分方程组,进行求解。
2.1. 货车模型的建立
在本文中,仿真模型建立的基础为神朔重载铁路运输的C80型煤矿专用敞车,采用ZK6转向架。整个货车被简化为一个由三大件组成的刚体系统,三大件包括车体和前后两个转向架 [5] 。模型主要部件包括车体、摇枕、承载鞍、前后轮对、侧架和一系、二系悬挂等 [6] 。
ZK6转向架主要由轮对轴箱装置、侧架以及弹簧悬挂装置组成。其中,弹簧悬挂装置的作用是减少线路不平顺对车辆各种振动的影响,包括一系悬挂和二系悬挂。转向架的模型如图1所示。
在转向架的基础上建立货车的车体模型,需要定义承载鞍及其铰接,一系力及支挡,虚车体及其铰接,摇枕及其铰接,以及二系力、旁承力、心盘力、交叉拉杆力等,最后定义整车模型。建立C80的整车模型如图2所示。
2.2. 轨道不平顺模型
轨道不平顺是左右两股钢轨的实际位置和理想位置在高低和左右方向上的几何尺寸偏差 [7] ,由于钢轨材料和制作工艺等原因,在轨头表面会产生原始不平顺,当重载货物列车通过的时候,在特定的频率下轮轨有可能发生共振现象,这种垂向共振和钢轨波磨的产生关系密切,因此在建模过程中需要引入不平顺激励。经过对比分析得知,本文选用美国五级谱作为轨道不平顺模型来进行仿真 [8] 。
2.3. 小半径曲线线路模型
仿真模型的线路参数选取自神朔铁路现场某产生钢轨波磨区段的小半径曲线数据,其具体参数如下:1) 缓和曲线长度:设置为100 m;2) 圆曲线半径:设置为400 m;3) 曲线超高:设置为110 m;4) 圆曲线长度:设置为200 m。
2.4. 现场测试及模型的可靠性验证
2018年4月在山西忻州神朔重载铁路河东运输段上行的尧圪台工区进行了钢轨波磨现场测试试验,试验结果可用于模型可靠性的验证。试验里程为DK125~DK125 + 100 km。现场测试情况和试验数据如图3所示。
 (a) 现场测试图
(a) 现场测试图  (b) 轮轨力时程图
(b) 轮轨力时程图
Figure 3. Field test map of Shenshuo heavy-haul railway
图3. 神朔重载铁路现场测试图
使用FAMOS软件对测试的轮轨力进行统计分析,并与仿真结果进行对比,如表2所示。

Table 2. The field test and the simulation analysis result contrast statistics
表2. 现场测试与仿真分析结果对比统计
由表2对比可以看出,仿真计算结果和现场试验数据相差不大,从而验证了本分析模型的可靠性。
3. 钢轨波磨的产生机理研究
对神朔重载铁路的调研发现,钢轨波磨主要出现在小半径曲线地段的内股钢轨上。为了更好的揭示曲线钢轨波磨的产生机理,以下分析将通过现场试验得到的波磨数据与仿真模型进行对比分析,从不同角度进行波磨的产生机理研究。
3.1. 钢轨波磨产生机理的频域分析
试验地点选在神朔铁路河东运输段上行的尧圪台工区,试验里程为DK125~DK125 + 100 km,本文采用CAT钢轨波磨测量仪等实验仪器对该地段的波磨情况进行了精确测量。
实验测量结果如图4所示。
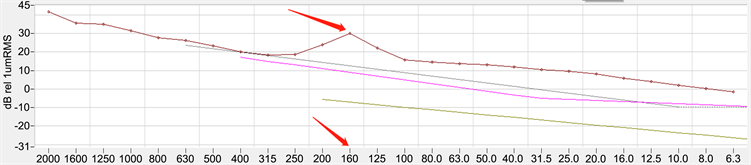
Figure 4. The curve of characteristic wavelengths
图4. 特征波长曲线
通过试验测得现场波磨的特征波长为160 mm,根据通过频率的公式:

式中:v为货车车速,由现场数据可得速度为50 km/h~60 km/h,λ为特征波长。
可以得到钢轨波磨的特征频率:

根据反馈共振理论,轨头表面的原始不平顺将会激起轮轨的振动,当重载货物列车通过时,由于各种原因,那些与垂向振动固有频率相差悬殊的波长成分会被磨掉,由此产生具有特征波长的波磨 [9] 。所以在该理论下,钢轨表面具有特征波长波磨的通过频率应该和由初始不平顺引起的蠕滑振动有关。因此利用SIMPACK软件模拟当时的曲线通过情况,在美国五级谱的轨道不平顺激励作用下,让货车模型通过小半径曲线,车速设置为60 km/h,曲线要素和初始曲线要素相同,仿真时间为30 s,采样频率设置为500 Hz。经过离线积分可得轮轨的纵向和横向蠕滑率如图5、图6所示。采用FTT (快速傅里叶变换)对纵向和横向蠕滑率曲线进行数字滤波。傅里叶分析的方法是将信号分解成不同频率的正弦函数,然后将这些函数进行叠加。将横向蠕滑率(纵坐标)和时间(横坐标)的二维数组输入Origin程序,在时域内使用FFT,并将所得结果以对数log10的形式显示,所得结果如图7所示。设置一对照组:在其他变量完全相同的情况下,不施加轨道不平顺,仍以同样的速度在曲线上运行,仿真时间30 s,采样频率500 Hz。经过离线积分可得轮轨的纵向和横向蠕滑率如图8和图9所示。
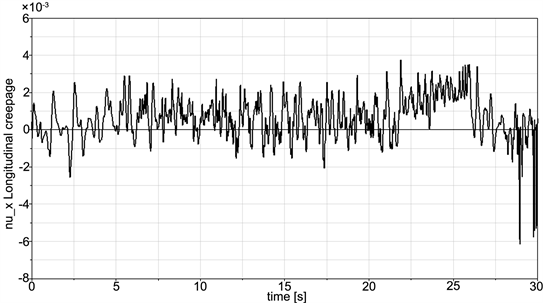
Figure 5. The characteristic curve of longitudinal creepage
图5. 纵向蠕滑率特征曲线

Figure 6. The characteristic curve of lateral creepage
图6. 横向蠕滑率特征曲线

Figure 7. The curve of lateral creepage frequency
图7. 横向蠕滑率频率曲线

Figure 8. The characteristic curve of lateral creepage (no excitation)
图8. 横向蠕滑率特征曲线(不添加不平顺激励)

Figure 9. The characteristic curve of longitudinal creepage (no excitation)
图9. 纵向蠕滑率特征曲线(不添加不平顺激励)
与前文处理方法相同,将横向蠕滑率(纵坐标)和时间(横坐标)的二维数组输入Origin程序,在时域内使用FFT,并将所得结果以对数log10的形式显示,所得结果如图10所示。

Figure 10. The curve of lateral creepage frequency (no excitation)
图10. 横向蠕滑率频率曲线(不添加不平顺激励)
根据添加激励的实验组经过傅里叶变换的横向蠕滑率曲线(图7)可以得到,在横坐标位于1至2之间曲线峰值,经过对数运算可知峰值出现频率在10 Hz~100 Hz之间,与前文在经过现场实测所得的钢轨波磨的频率的数据相对应,剔除坏值和误差,可以发现由轨道原始不平顺引起的轮轨横向蠕滑率的特征频率与钢轨波磨的通过频率十分接近。
根据不添加轨道不平顺激励的对照组的横向蠕滑率频率曲线可知,峰值出现在横坐标小于1的范围内,经过对数运算,可知在该情况下,峰值出现频率低于10 Hz。结合垂向振动理论的原理可知,当重载货车通过时,与轮轨垂向振动固有频率相差悬殊的波长成分被磨掉,随着时间的变化,不平顺波长的带宽逐渐减小,垂向振动被激化,由此产生特征波长的波磨。而不添加轨道原始不平顺激励的对照组的结果表明蠕滑率与波磨的波长和频率均无明显关系。由此得以证明轮轨间的初始不平顺会激起轮轨间的振动,导致钢轨波磨的产生。
3.2. 曲线地段内轨与外轨的对比
利用SIMPACK模型进行仿真,使用不添加原始不平顺激励的轨道模型,目的是尽量减少其他次要因素的干扰,便于直观地看出曲线内外轨的差异。工况选取标准工况。
首先对比内外轨的轮轨横向力,其特征曲线如图11所示。

Figure 11. The diagram of lateral forces of internal and external rails
图11. 内外轨横向力对比图
曲线中,黑色实线为右轨(内轨),红色虚线为左轨(外轨),从图11中可以较清晰地看到在通过小半径曲线时,内轨所受的横向力要远大于外轨所受的横向力。
接下来对比内外轨钢轨的磨耗指数,其曲线如图12所示。
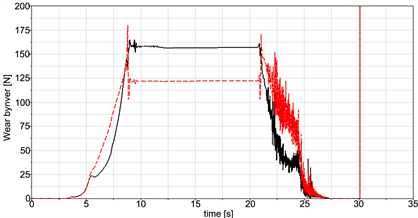
Figure 12. The diagram of wear number of internal and external rails
图12. 内外轨磨耗指数对比图
轮轨的磨耗指数能够直观地体现出轮轨的磨耗程度。在曲线中,内轨的磨耗指数要大于外轨,这表明内轨因磨耗而消耗的能量消耗要大于外轨,所以在曲线上内轨的波形磨耗要比外轨严重。
当重载货物列车通过曲线地段时,由于离心力的作用,外侧的车轮轮缘会紧贴外股钢轨,两者在横向运动的同时也会产生一定的相对滑动 [10] 。当轮对的横向自振频率和轨枕的通过频率接近或成正比时,轮对会产生一个横向的振动,从而导致内股轮轨间发生周期性的相对滑动,该滑动将会进一步造成内股钢轨顶面的波浪形不均匀磨损,这就是曲线内股钢轨波磨的产生原因。
4. 钢轨波磨的影响因素分析
线路曲线段由两个曲率和超高不断变化的缓和曲线、一个曲率及超高均固定的圆曲线组成。当车辆从直线地段进入小半径曲线轨道的时候,由于受到各种激扰,其曲线通过性能会受到多种因素的影响,主要有轨道结构参数、轮轨几何型面和转向架结构等 [11] 。其中,轨道结构参数主要有外轨超高、曲线半径、缓和曲线长度和轨底坡等 [12] 。如果这些曲线参数设置不当,将直接导致轮轨接触关系发生改变,这将可能是产生轮轨波磨的因素之一。因此,找出不同曲线参数对钢轨波磨的影响,合理设置轨道曲线对减缓钢轨波磨具有重要作用。
根据神朔重载铁路河东运输段的某小半径曲线特点,选取的基本工况如下:货车运行速度为60 km/h,曲线半径为400 m,外轨超高为110 cm,轨底坡为1/40,缓和曲线长度为Ll = L2 = 100 m。
4.1. 曲线半径的影响
利用SIMPACK仿真分析不同曲线半径对重载货车钢轨波磨的影响,基本工况曲线半径取值分别为300 m,400 m,500 m,600 m和700 m,其他参数不变。
1) 磨耗指数
计算的不同曲线半径下的磨耗指数如图13所示。

Figure 13. The curve of wear number with radius
图13. 磨耗指数随曲线半径变化曲线
从图13中可以看出,随着曲线半径的不断增大,内侧轮轨的磨耗指数不断减小,当曲线半径从300 m增加到700 m的过程中,磨耗指数有明显下降。
2) 轮轨横向力
分别提取不同曲线半径下前转向架的前轮对的右侧轮轨(内轨)的轮轨横向力,整理可得轮轨横向力随曲线半径的变化曲线如图14所示。

Figure 14. The curve of lateral force with radius
图14. 轮轨横向力随曲线半径变化曲线
从图14中可以看出,随着曲线半径的不断增大,轮轨横向力逐渐减小。
2) 脱轨系数
脱轨系数是行车安全评价指标的一项重要内容。脱轨系数Y/Q是轮轨横向力Y与轮轨垂向力Q的比值。根据我国国家相关标准规定,为保证行车安全稳定,防止列车脱轨,脱轨系数应有如下两种限度: Y/Q = 1.2为危险限度; Y/Q = 1.0为容许限度 [6] 。现分别提取不同曲线半径下前转向架的前轮对的右侧轮轨(内轨)的脱轨系数,整理可得脱轨系数随曲线半径变化曲线如图15所示。
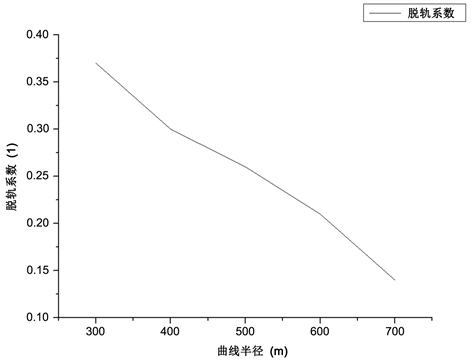
Figure 15. The curve of derailment coefficient with radius
图15. 脱轨系数随曲线半径变化曲线
由以上数据可得出以下结论:
随着曲线半径的增大,轮轨磨耗指数、轮轨横向力以及脱轨系数都逐渐减小。可见,小曲线地段将会产生更大的轮轨作用力和磨耗作用,而且脱轨系数较大,对行车安全不利。因此,在重载铁路修建过程中,应尽量少设置小半径曲线,并对小半径曲线段的钢轨采取及时打磨等特殊的养护维修方法,以减少钢轨磨耗带来的危害,提高钢轨使用寿命,有利于行车安全。
4.2. 外轨超高的影响
曲线的外轨超高是指曲线内外轨顶面之间设置的水平高差。曲线超高可以使列车的自身重力产生一个向心的水平分力,可以抵消离心惯性力。当超高设置不当时,容易导致钢轨的磨耗加深。本节模拟的超高变化基本工况分别为90 mm、100 mm、110 mm、120 mm、130 mm。
1) 磨耗指数
计算的不同外轨超高下的磨耗指数如图16所示。

Figure 16. The curve of wear number with elevation of outer rail
图16. 磨耗指数随外轨超高变化曲线
从图16可以看出,随着曲线超高的增大,磨耗指数有一定的增长。
2) 轮轨横向力
分别提取不同外轨超高下前转向架的前轮对的右侧轮轨(内轨)的轮轨横向力。整理可得轮轨横向力随外轨超高的变化曲线如图17所示。

Figure 17. The curve of wear number with elevation of outer rail
图17. 磨耗指数随外轨超高变化曲线
从图17可以看出,随着曲线超高的增大,外轨横向力有一定增长的趋势,但变化不明显。
3) 脱轨系数
经过数据处理,脱轨系数在超高改变的条件下变化不大,始终稳定在0.33左右,故在此不再赘述。
由上述数据可知:在外轨超高从90 mm增大至130 mm的过程中,轮轨横向力和磨耗指数都有一定增长,但是变化幅度不大,变化不明显。因此,曲线超高过大会使钢轨的磨耗程度加深,降低钢轨使用寿命。所以降低外轨超高在一定程度上可以使轮轨磨耗情况得以减缓,能够较有效地提高列车的曲线通过能力。
4.3. 货车速度的影响
为了更好的研究钢轨波磨的情况,减缓轮轨间的磨耗作用,需要考虑行车速度对钢轨波磨的影响。本模拟选取货车运行速度基本工况分别取值40 km/h、50 km/h、60 km/h、70 km/h和80 km/h。
1) 磨耗指数
计算的不同货车速度下的磨耗指数如图18所示。

Figure 18. The curve of wear number with speed
图18. 磨耗指数随行车速度变化曲线
从图18中可以看出,随着行车速度的提高,列车的磨耗指数也逐渐增大,说明轮轨磨耗也更加剧烈。
2) 轮轨横向力
计算的不同货车速度下的轮轨横向力如图19所示。
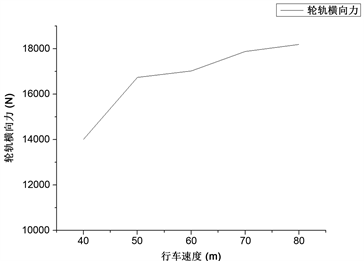
Figure 19. The curve of lateral force with speed
图19. 轮轨横向力随行车速度变化曲线
从图19中可以看出,随着行车速度的提高,列车的轮轨横向力也逐渐增大,说明轮轨作用更加密切,轮轨接头处更容易产生钢轨波磨。
3) 脱轨系数
经过数据处理,脱轨系数在车速的条件下变化不大,始终稳定在0.375左右。
由上述数据处理与计算可知,随着货车速度的增大,内轨横向力与磨耗功率均呈增大的趋势。而且速度越大钢轨的波磨程度也越严重,不利于重载列车的安全和运营,因此应该根据实际情况设置曲线通过速度,以减轻钢轨波磨的危害,并保证货车安全地通过小曲线地段。
5. 结论
论文建立小半径曲线C80型货车车辆–轨道耦合模型,对重载铁路钢轨波磨的产生机理和影响因素进行了系统的数值分析,得出如下结论:
1) 列车通过曲线时,当轨枕的通过频率与轮对的横向自振频率接近或成其整数倍时,轮对产生横向振动,导致内股轮轨间发生周期性的相对滑动,造成内股轨顶面的周期性的不均匀磨损,从而形成钢轨波磨。
2) 随着曲线半径的增加,轨道结构横向力和钢轨磨耗功率等都有较大幅度的降低。这表明曲线半径越大对减缓钢轨磨耗越有利,应尽量避免小半径曲线,建议曲线半径值大于等于500 m。
3) 随着外轨超高的减小,内轨横向力和磨耗指数都有所降低,但外轨横向力变化不大。总体来说,超高量的降低在一定程度上使得内外轨的轮轨磨耗情况得以缓解,有效地提高了列车曲线通过能力。
基金项目
中国神华能源股份有限公司科技创新项目(神朔科技合[2017]7号)。