1. 引言
随着微分方程理论的发展和完善,分数阶微分方程作为一个新兴的研究领域,越来越受各界重视。如在流体力学、粘弹性、类扩散的扩散运输、医学超声检测、电气工程、生物工程学、控制理论等众多领域 [1] [2] [3] 。
微分方程的振动性已经被广泛研究 [4] [5] [6] 。近年来,一些学者在许多论文中研究了各类分数阶常微分方程和分数偏微分方程解的振动性 [7] - [12] 。但是到目前为止,关于带脉冲的分数阶微分方程解的振动性质的研究尚且很少。最近,A. Raheem和Md. Maqbul研究一类分数阶脉冲微分方程的解的振动性 [13] 。
本文的目的是研究如下一类具有多个时滞的中立型脉冲分数阶偏微分方程解的振动性:
(1)
边界条件满足:
(2)
其中
,且是常数,
表示Riemann-Liouville正半轴分数阶微积分定义下函数
关于变量t的
阶微分, α 是在
上的有界域,其边界
是光滑的,且
,
,
为拉普拉斯算子,n为边
的外法线向量,
,且强迫项
,PC表示以
为第一类间断点且在该处左连续的分段连续函数类。并且假设
, τ 为常数,
。问题(1)与(2)的解
、
是以
为第一类间断点且在该处左连续的分段连续函数,
。在这里,
,
。以下条件在脉冲点成立, 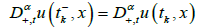 。
。
在本文中,我们总假设以下条件成立:
(H1): 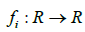 为连续函数,且对常数
,有
,且
;
为连续函数,且对常数
,有
,且
;
(H2):
,且满足 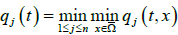 ;
;
(H3):
,且满足
;
(H4):
。
为了方便起见,我们记:
(3)
2. 预备知识
定义1 问题(1)与(2)的一个非零解
在区域G内是非振动的,如果存在一个常数
,使得在
,始终有
或者
。否则称振动的。
定义2 [2] 在Riemann-Liouville正半轴上的分数阶微分定义下,对于
关于变量t在正半轴上逐点定义的
阶微分表示如下:
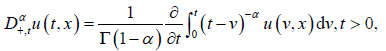 (4)
(4)
其中
,
表示gamma函数,并定义为
。
引理3 [1] 若函数
满足:
其中
为常数。那么
。
引理4 [4] 若如下问题的最小特征值
为正:
其中 λ 是一常数。则相关的特征方程
在
,也为正。
引理5 [6] 假设以下不等式成立:
其中,
, 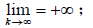 ;
,
;
, 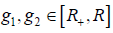 ,
是常数。那么
,
是常数。那么
3. 主要结果及证明
定理3.1 假设条件(H1)~(H4)成立,如果分数阶脉冲微分不等式
(7)
(8)
没有最终正解,并且分数阶脉冲微分不等式
(9)
(10)
没有最终负解,那么问题(1)与(2)的每一个非零解
在G内都是振动的。
证明:(用反证法)假设
是问题(1)与(2)的一个非振动解。不失一般性,我们假设
是问题(1)与(2)的最终正解,即存在
,当
,使
,
。
(I) 当
,对(1)的第一个方程,两边同时对x在有界域
上积分得到:
(11)
根据Green公式,结合边界条件(2)和假设(H4)得到:
(12)
(13)
根据条件(H1)和(H2)得到:
(14)
结合(11)~(14)可得:
(15)
(II) 当
,对(1)的第二个方程,两边同时对x在有界域
上积分
(16)
即得到
(17)
根据引理3,并由(16)可知
(18)
类似地,由式(17)可知
(19)
结合(18)~(19),并根据条件(H3),有
(20)
因此,由脉冲微分不等式(15)与(20)可知,函数
是分数阶脉冲微分不等式(7)~(8)的最终正解。与假设条件相矛盾。
另一方面,如果
是问题(1)与(2)在G内的最终负解,由相似的的方法,可知函数
是分数阶脉冲微分不等式(9)~(10)的最终负解。与假设条件相矛盾。证毕。
定理3.2 假设条件(H1)~(H4)成立,如果存在
,满足
(21)
其中,
,
,存在 μ1 ≥ 0 ,满足
(22)
并且
(23)
那么,问题(1)与(2)的每个解在G内是振动的。
证明(反证法):证明该定理,先证明分数阶脉冲微分不等式(7)~(8)没有最终正解且分数阶脉冲微分不等式(9)~(10)没有最终负解。不失一般性,假设
是分数阶脉冲微分不等式(7)~(8)的最终正解,那么存在
,使得
,
,
。
由式(7)和引理3,可得:
(24)
在这里,令
(25)
把(25)代入(24),有
(26)
即有
所以有
对任意 j∈1,2,, n ,有
(27)
由脉冲微分不等式(20),结合上述式子,有
由引理5,可得
(28)
所以
当
,根据条件(22),由上式可得
这与
矛盾。证毕。
另一方面,由类似方法,当
,根据条件(23),由上式可得
证毕。
4. 举例
假设条件(H1)~(H4)成立,考虑如下多时滞的分数阶脉冲偏微分方程
(29)
边界条件满足:
(30)
其中,
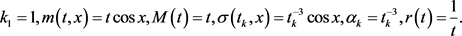
显然可得
且有
因此,满足定理3.2的所有条件。故问题(29)~(30)的解为振动解。
参考文献
NOTES
*通讯作者。