1. 引言
齿轮传动在当代工业制造业里广泛应用,喷丸工艺是一种很好的大幅度提高齿轮的弯曲疲劳强度的措施。喷丸齿轮表面微观形貌对润滑特性的影响很大,当前粗糙度影响润滑的研究重点放在了机加工形貌对润滑特性的影响,而对齿面喷丸强化后形成的粗糙形貌对润滑的研究仅仅停留在试验阶段。
主要研究弹丸直径和喷丸强度对20Cr2Ni4A钢试样表层显微组织、残余奥氏体、残余应力、显微硬度、表面形貌、摩擦磨损性能和冲蚀性能的影响。利用ABAQUS软件研究了弹丸直径和喷丸速度对9310钢表层残余应力场和表面粗糙度的影响 [1] [2] 。表面喷丸强化技术是工程上应用最广的表面强化技术之一。通过喷丸强化技术在工件表面引入残余压应力,并改善工件表层组织结构,使工件表面的硬度和强度、抗疲劳性能以及抗应力腐蚀性能等均能得到显著提高 [3] [4] 。Nobre、Coelho等人研究发现齿轮经过喷丸强化处理后,表层显微硬度得到提高,组织得以改善,并产生较大的残余压应力,表面完整性得到改善,因此疲劳寿命得以提高 [5] 。S. A. Meguid和A. Gariepy等 [6] 建立了具有四个对称面的喷丸强化元胞模型,利用少量板材单元模拟了大量弹丸对板材的撞击过程。H. Y. Miao等人 [7] 采用类似的模型研究了多个喷丸工艺参数对残余应力分布的影响规律。建立了无对称面的三维喷丸强化模型,研究了弹丸撞击位置随机分布情况下,喷丸强度、覆盖率、粗糙度与弹丸数目的定量关系。
本文以揭示齿面喷丸微观形貌为目标,拟建立一种合理的描述齿面喷丸的微观形貌的数学模型,使其不局限于实验性的探究,为齿轮全齿喷丸强化后润滑分析做理论支撑,对于改善这种工况下的润滑性能有很强的指导价值和现实意义。
2. 有限元分析
本文运用ABAQUS/Explict有限元软件对喷丸强化进行有限元仿真,再利用Matlab对表面微观形貌进行数值模拟 [8] 。目的是为了获取齿轮喷丸后金属表面微观形貌的数值模型。同时也获得机加工表面形貌的数值模型。
2.1. 喷丸强化有限元模型建立
目前多弹丸喷丸强化有限元模型分为几种,本文借鉴9丸粒模型的建模方法,喷丸强化仿真采用了常用的25丸粒模型喷丸、典型的3D四层49丸粒偏置模型 [9] 。如图1所示。
2.2. 覆盖率对比
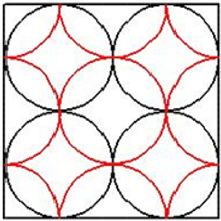
25丸粒模型喷丸强化时,喷丸形成的凹坑规则明显且独立,没有相互影响,因此可以单独研究凹坑对弹流润滑特性的影响。49丸粒模型喷丸强化时,齿轮表面原始形貌被完全破坏,其他影响喷丸效果的因素不再考虑,此时对喷丸齿轮弹性流体润滑的研究分析是最全面,最真实的(图2)。
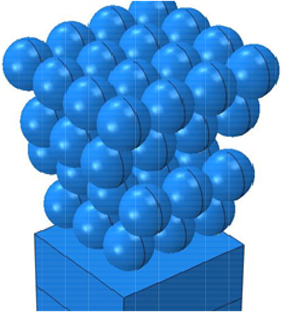
Figure 1. Finite element model of 49 pellets bias
图1. 49丸粒偏置有限元模型
 (a)
(a) 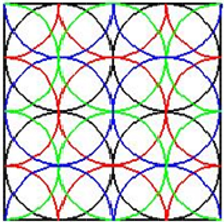 (b)
(b)
Figure 2. Comparison of coverage rate of two models: (a) 25-pellet model; (b) 49-pellet model
图2. 两种模型覆盖率对比:(a) 25丸粒模型;(b) 49丸粒模型
2.3. 参数选取
试件材料为40Cr钢。弹丸材料选择铸钢丸。具体参数选择如下:
目标靶材力学性能参数:弹性模量210 Gpa、密度7800 Kg/m3、泊松比0.3、初始屈服应力800 Mpa、硬化模量1000 Mpa。库仑摩擦系数为0.2。
弹丸力学性能参数:弹丸直径0.5 mm、弹性模量210 Gpa、密度7800 Kg/m3、泊松比0.3。选择刚性体模拟,喷丸初始速度50 m/s。
2.4. 单元的选择和网格的划分
网格细化会造成计算时间长,消耗大量的内存和存储空间,同时为了让表面形貌模拟精确,尽可能的细化靶材表面网格。同时综合考虑后文Matlab数值模拟分析所需时间与精度,表面网格划分设置为100 × 100。从接触表面往下,将靶材划分成了四份,越往底层网格变得越稀疏。在不影响分析结果的条件下,提高运算效率,减少运行时间。如下图3所示。

Figure 3. Meshing of shot peening finite element model
图3. 喷丸有限元模型网格划分
2.5. 载荷和边界条件
由于本例只是截取的齿轮表面的一部分,因此四个侧面实际上并不是边界,这里本例将侧面法向位移设置为0,“固定”四个侧面。仿真采用库仑摩擦模型对弹丸与工件间相互接触进行描述,并设置摩擦系数为0.2。
3. 表面形貌描述
3.1. 表面微观形貌参数及表征方法
表面微观形貌是利用几何特征或者波峰波谷来表征,具体表达参数包括表面粗糙度、表面波纹度、表面纹理几何特征和表面缺陷。在机械制造领域,通常用表面粗糙度来衡量表面形貌的加工质量和精度。
3.2. 机加工表面形貌模拟
为了对比喷丸强化前后表面微观形貌的变化,本文利用Matlab模拟多个机加工表面形貌 [10] [11] 。假定齿面粗糙度分布函数为
,RS为余弦函数粗糙峰的幅值。其中RS = 3.2 μm比RS = 1.6 μm粗糙峰峰值非常大,波动情况一致(图4)。
3.3. 喷丸有限元仿真后表面形貌
3.3.1. 25丸粒模型的表面形貌
25丸粒模型中ABAQUS分析结果如图5所示。靶材微观形貌如图6所示。可以看出弹丸和靶材表面发生了碰撞并全部反弹,在靶材表面留下了许多规则的弹坑,这是因为弹丸是规则排列的。一个弹丸形成一个弹坑,弹坑之间没有形成相互的影响,25丸粒模型并没有完全改变了齿轮表面的微观形貌,在弹坑与弹坑之间,还有许多“平面”区域。本文研究25丸粒模型的喷丸模型,可以更直观的观察出单个弹坑对喷丸齿轮弹流润滑特性的影响。
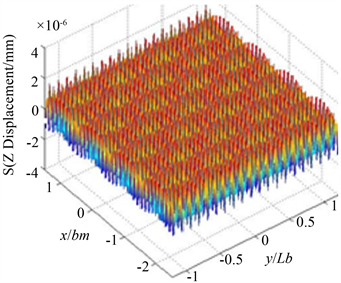 (a) RS = 3.2 μm
(a) RS = 3.2 μm  (b) RS = 1.6 μm
(b) RS = 1.6 μm
Figure 4. Machining surface morphology
图4. 机加工表面形貌
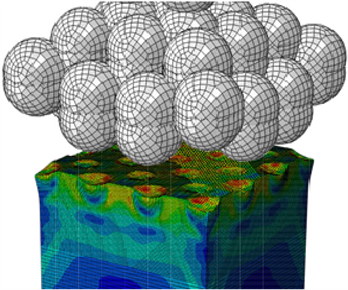
Figure 5. Finite element calculation of 25-pellet model
图5. 25丸粒模型喷丸有限元计算结果
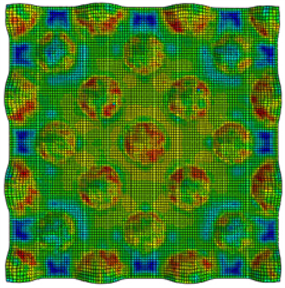
Figure 6. Surface result of 25-pellet model shot peening target
图6. 25丸粒模型喷丸靶材表面结果
3.3.2. 49丸粒模型的表面形貌
49丸粒模型中ABAQUS分析结果如图7所示。金属摩擦表面形貌如图8所示。可以看出弹丸和靶材表面发生了碰撞并全部反弹,在靶材表面留下了许多规则的弹坑,这些弹坑相互叠加,相互影响,完全改变了齿轮表面的微观形貌。形成了喷丸强化微观表面标志性橘皮凹坑形貌。真实的喷丸强化覆盖率更高,喷丸强度更大,凹坑相互影响更多,且不规则,凹坑更加细密平滑。但总体形貌特点和此例中的表面形貌类似,此例中的表面形貌可以作为后续喷丸齿轮弹流润滑分析的喷丸强化后齿轮表面微观形貌研究依据。
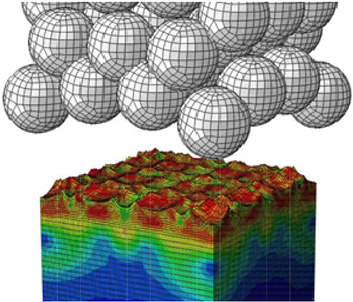
Figure 7. Finite element calculation results of 49-pellet model
图7. 49丸粒模型有限元计算结果

Figure 8. Surface results of 49-pellet model targets
图8. 49丸粒模型靶材表面结果
4. 结论
本文首先对有限元理论在喷丸强化中的应用进行了比较详细的阐述,包括有限元软件的选择、有限元软件的建模,参数选取,网格划分,沙漏控制等有限元仿真时的关键技术;建立了25丸粒和49丸粒模型两个偏置多丸粒喷丸强化模型;对靶材采取了喷丸强化有限元的仿真,得到了喷丸强化后有限元模拟仿真结果。结果显示:25丸粒模型一个弹丸形成一个弹坑,弹坑之间没有形成相互的影响,25丸粒模型并没有完全改变齿轮表面的微观形貌。49丸粒模型中弹丸和靶材表面发生了碰撞并全部反弹,在靶材表面留下了许多规则的弹坑,这些弹坑相互叠加,相互影响,完全改变了齿轮表面的微观形貌,形成了喷丸强化微观表面标志性橘皮凹坑形貌,凹坑更加细密平滑。
参考文献