1. 引言
TiB2具有熔点高、硬度大、化学稳定性好等优点,被作为硬质工具材料、磨料、防护材料以及硬质合金添加剂 [1] 。同时TiB2具有优良的电性能,常作为惰性电极材料和高温电工部件 [2] [3] 。近年来,MgB2超导体的发现引起人们对MB2类硼化物电子结构的极大关注,对MB2类的电子理论做了很多研究 [4] 。此外,TiB2阴极涂层是TiB2材料应用于现行铝电解槽中最主要的方式,也是最有希望成为用于基于惰性电极系统的新型铝电解槽的惰性可润湿性阴极材料。这就需要对TiB2的晶格动力学性质做深入研究。然而目前对TiB2的研究主要集中于电学性质。计算表明不同层Ti原子的3d和B原子2p的杂化使得TiB2具有赝带隙(pseudogap) [5] ,TiB2 (0001)表面都不发生重构,但表面几层原子都出现明显的弛豫现象 [6] 。由于对TiB2的光学、声学性质的第一性原理的理论研究则较少,本文计算了TiB2的电子结构,光学特征以及晶格动力学性质,为TiB2在润湿性阴极材料的应用提供理论依据,解释了TiB2不具备高温超导性的原因。
2. 计算模型与方法
TiB2密度为4.26 g/cm3,属六方晶系,空间群为P6/mmm,晶格常数为a = b = 0.3028 nm,c = 0.3228 nm,α = β = 90˚,γ = 120˚。六方简单原胞中Ti原子坐标为(0 0 0),占据六棱柱的顶角和底心位置。B原子坐标为(1/3, 2/3, 1/2)和B(2/3, 1/3, 1/2),位于Ti原子构成的三棱柱中心,在XY平面的投影位置位于Ti原子组成的等边三角形的重心。在TiB2晶体中,B原子面和Ti原子面交替构成二维平面网状结构 [7] ,如图1(a)。图1(b)为计算的TiB2模型。

Figure 1. Crystal structure of TiB2 (gray ball is Ti atom; pink ball is B atom). (a) TiB2 crystal; (b) calculation model
图1. TiB2晶体结构(灰色球为Ti原子,粉色球为B原子)。(a) TiB2晶体;(b) 计算模型
由于理想的TiB2单晶没有杂质等缺陷,所以TiB2晶体符合周期性边界条件,计算由CASTEP (Cambridge serial total energy package)完成。采用基于平面波基组的赝势从头算方法,在晶体周期性势场中,采用三维周期边界条件,将多电子体系用平面波函数展开表示,采用超软赝势来描述离子实与价电子之间的相互作用 [8] 。在倒易的k空间中,平面波截止能(Ecut)选取为770 eV。交换-关联能采用GGA,修正方法(PBE) [9] 。系统的总能量和电荷密度在布里渊区的k矢量选取为8 × 8 × 10,以保证体系能量和构型在平面波基水平上收敛。在自洽场运算中,采用了Pulay密度混合法,自洽场设为2.0 × 10−6 eV/atom。采用了BFGS算法对结构优化,优化参数有四个:原子间的作用力的收敛标准为0.05 eV/nm;单原子能量的收敛标准为5.0 × 10−6 eV;晶体内应力的收敛标准为0.01 GPa;原子最大位移收敛标准为5× 10−5 nm [10] 。四个参数均达到收敛标准即完成结构优化。参与计算的价态电子为Ti3d24s2,B2s22p1。使用norm-conserving赝势计算模型的光学性质,计算k矢量为8 × 8 × 3,未经能隙修正。
3. 计算结果与讨论
3.1. TiB2结构优化
利用BFGS算法将图1(b) TiB2结构优化后计算得到TiB2的各项物理参数,如表1。

Table 1. Calculation results of various parameters of TiB2
表1. TiB2的各项参数计算结果
一般认为LDA计算存在过结合,即晶格常数偏小,而GGA则相反,即晶格常数偏大的现象。从本文计算(GGAa)可知,采用GGA计算得到六方晶体的a,c值均偏大,这与文献 [9] 计算结果一致。计算的体弹性模量值比实验值小,泊松比在六方晶体结构中沿三个方向的数值不同,最大的是沿Z方向,最小的是沿X、Y方向,平均值为0.24,表现出各向异性。由此可预测沿B原子平面的弹性模量(X或者Y方向)较大。石墨、MgB2、h-BN等层状结构的晶体,因各向异性,其力学参量在X和Y组成的平面上差别不大,但和Z轴相比差别很明显。计算表明TiB2具有层状结构晶体的特征。
3.2. TiB2能带和态密度分析
在分析TiB2能带结构和DOS之前先分析TiB2的对应元素价电子轨道的群分解和可能形成的化学键。计算中Ti原子价电子轨道为3d和4s,考虑到3s和3p轨道对整个计算结果有影响,因此这两个轨道作为半芯轨道也记入计算;B原子价轨道是2s和2p。TiB2空间群对应的原子点群是D6h群,价电子轨道在D6h点群中分别属于不同的不可约表示,如式1 (Equation (1))。
(1)
根据分子轨道理论,原子间轨道在能量接近且对称性一致条件下有可能成键。因此从晶体轨道不可约表示来看,s轨道和Ti
对称性一致,B2p轨道和Ti3d不可约表示不同,从轨道能量上考虑B2s可能和Ti
形成化学键。计算TiB2晶体能带结构和态密度(density of states, DOS)如图2。图2(a)中费米能级附近的两个峰为最高峰,表现出赝带隙 [8] 。费米能级计算值−1.096 eV。总态密度(total density of states, TDOS,图2(b))和分波态密度(partial density of states,PDOS,图3)分析表明,在费米能级附近存在较大态密度,晶体导带和价带发生重叠,总态密度峰主要对应Ti3d和B2p的态密度。这说明TiB2导带和价带电子主要由Ti3d和B2p轨道的价电子构成。图3为TiB2中元素态密度图。从B的PDOS (图3(b))可看到2s和2p轨道重合,这与前面分子轨道理论结论不一致,这需引入Pauling杂化轨道理论来解释。由于TiB2晶体中六方网格结构的B原子为sp2杂化,sp2杂化可约表示为
,因此s和p轨道DOS谱是重合的,但中心并非一致。DOS谱中能量较低的部分B的2s轨道权重大,Fermi面附近2p轨道权重大。新产生的轨道同时具有A1g和E1u的对称性,可以和Ti的3d轨道形成化学键。这样原来分属不同不可约表示的2p和3d轨道可发生作用,对应轨道为B的2s,2px,2py以及Ti
。

Figure 2. Electrical properties of TiB2 (a) energy band; (b) density of states
图2. TiB2电学性质(a) 能带;(b) 态密度

Figure 3. Electron state density diagram of element in TiB2 (a) Ti; (b) B
图3. TiB2中元素电子态密度图(a) Ti;(b) B
Fermi面以上DOS最高峰主要来自于Ti3d轨道,而其他两组属于
和
不可约表示。价带顶部主要是B2p轨道,从化学键性质分析是B平面sp2σ键。根据对MgB2早期计算结果表明在导带顶部的高能部分,主要构成是sp2σ反键态,在TiB2中也是这样。B2pz和其他轨道的不可约表示不同,垂直于B平面pz轨道单独形成连续π键,这对于整个B原子平面导电性有影响。这些价电子通过离域π键在电流的作用下可在TiB2晶体中迁移,因此在TiB2晶体中电子的传输决定了其具有类似于金属自由电子的导电性能 [11] 。TDOS (图2(b))中π键态在σ键和反σ键态之间,所有这些化学键能级之间的跃迁会在光学性质中体现,在2.4节中将进一步分析。考虑同一Ti原子层中Ti原子间,以及不同Ti原子层间的作用,从轨道的对称性上考虑,化学键能级之间的跃迁是可能的,比如Ti原子层内的
轨道之间,以及层间的
轨道。但由于TiB2晶体中Ti原子间距离较远,这种作用很弱。
3.3. TiB2电子密度和电子云轨道分布
TiB2的差分电子密度结果如图4。用等高线表示TiB2 (11~20)晶面上电子密度分布,颜色较深区域电子密度大,反之较小。可以看出,B-Ti键为离子键和共价键混合 [12] 。

Figure 4. Electron density of plane TiB2 (11 - 20) (a) TiB2 (11 - 20); (b) electron density
图4. TiB2 (11~20)面电子密度(a) TiB2 (11~20)晶面;(b) 电子密度
TiB2的电子云轨道分布计算值如表2,计算表明TiB2为离子晶体,B带负电性,Ti带正电性,这与电子密度一致。B原子得到1个电子后发生sp2杂化,形成B−与B−之间σ键;B−中未参与杂化的另一2pz电子之间以离域π键的形式相结合。如2.2节指出的,TiB2与MgB2类似,金属原子和B原子层间发生了明显的电荷转移,这种电荷转移对MgB2而言一定程度上增强了电子-声子间的作用,提高了Cooper电子对的浓度,有利于提高超导转变温度 [13] 。而后面2.5节的计算表明这个假设只对MgB2成立,对TiB2不成立。在表3中Ti的s轨道只包含了4s成分,因Ti3s轨道作为半芯轨道引入赝势,在化学上为惰性,故不考虑。B2s和Ti4s轨道电子转移最明显,B2s电子转移主要原因为2s和2p杂化,而Ti4s电子转移给3d轨道(如
)。从重叠电子云轨道和对应原子间的键长来看,B原子间强烈的共价键对应短的键长和较大的电子云轨道数,而Ti和B之间更多的是一种离子相互作用,键长大,且重叠电子云轨道数小于0。

Table 2. Calculated values of electron cloud orbital distribution of TiB2
表2. TiB2的电子云轨道分布计算值
注:表2内Ti的s轨道的1.97个电子是3s和4s电子和,因4s电子基本失去,因此可认为1.97个电子都属于3s轨道。表内Ti的p轨道是3p和4p电子和,因3p是芯轨道,不参与化学键作用,因此可认为3p电子数为6,其余0.26个电子占据4p轨道。过渡金属里为(n − 1)dnsnp间能级差别不大,电子在这些轨道之间的转移很常见。

Table 3. Inter-band and intra-band transitions corresponding to TiB2 absorption peaks
表3. TiB2吸收峰对应的带间和带内跃迁
3.4. TiB2光学性质计算
使用norm-conserving赝势计算了TiB2的光学性质。反射率、吸收系数、折射指数和介电函数等结果如图5。反射率R(ω)反映了能带结构中导带和价带之间的跃迁。TiB2的光吸收计算值表明在0 eV~20 eV有7个比较明显的吸收峰,如图5(b)。超过20 eV属于等离子激发区域,没有考虑。所得到的介电函数实部ε1和虚部ε2如图5(d)。由图5(d)可知,ε1在频率为0对应的是TiB2的静态介电常数,计算值80。
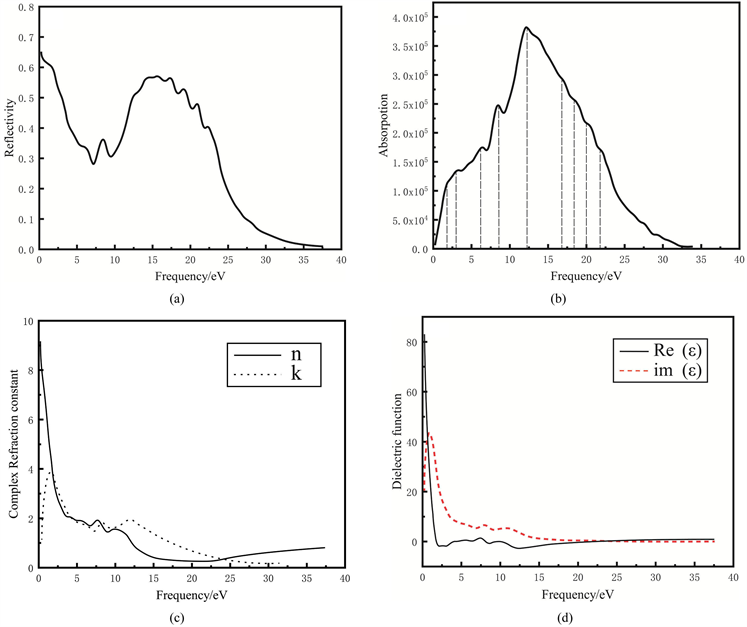
Figure 5. Optical properties of TiB2. (a) reflectivity; (b) absorption coefficient; (c) refractive index; (d) dielectric function
图5. TiB2光学性质。(a) 反射率;(b) 吸收系数;(c) 折射指数;(d) 介电函数
体系在较小波矢下对光电场的线性响应由复介电常数
决定。介电常数和晶体轨道在倒易空间特殊k点位置附近的跃迁机制有密切关系,在介电常数中虚部和实部曲线上的峰值对应晶体轨道最活跃的跃迁部分。在TiB2中考虑简化条件,偶极跃迁,并且是直接能带之间的跃迁,对应轨道有2p → 3d,3d → 4s以及2p → 4s,同时由于轨道的杂化,还包括了B原子之间sp2σ键态之间的跃迁,2πpz键态之间的跃迁。计算的电子结构中无论是带间还是带内跃迁频率都远超过声子频率,使用的方法是单电子近似方法,故仅考虑电子激发。从量子力学的观点看,带间跃迁光吸收过程是电子在辐射电磁场微扰作用下从低能态跃迁到高能态过程,因此可以得到对应的跃迁,如图2(a)、图2(b)中箭头和表3。
3.5. TiB2声学性质计算
声子谱是TiB2晶格动力学的核心内容,利用声子谱不仅可以计算晶体的热力学性质,还可以考察TiB2晶体结构的稳定性。计算声子谱的关键是得到原子之间的力常数,CASTEP采用流行的线性响应理论来解决此问题。对平衡原子在简谐近似下作微扰,微扰后计算体系的总能量,力常数通过对体系总能量作关于原子位置的二次导数得到。本文计算的声子谱如图6。根据晶格动力学理论,TiB2晶体结构包含3个原子,因此有9个振动自由度,在声子谱中对应9条色散关系。在声子谱中可看到9条色散曲线,其中震动频率低于400 cm−1的三支是声频支,在Brillouin中心点Γ (图6中G)处是三重简并的。在Z以及F点,声频支分裂为下二上一的形式,对应横声频支(TA)和纵声频支(LA),剩余的6个色散关系均为光频支。光频支分裂很明显,频率较低的部分是横光频支(TO),最上面的两条是纵光频支(LO),值得注意的是在TO中有一条色散关系沿F-Q方向和LO耦合作用比较明显,从相关晶格动力学理论可知,该色散关系主要来自于B原子面。计算的TiB2声频支在Brillouin区中心出现的小于0的角频率原因是交换-关联能函数在实空间的计算破坏了晶体的平移不变性。通过对声子谱态密度的分析,发现所有的B原子对高频部分贡献最大,声频部分Ti原子的作用明显,其原因为B原子层中相互作用要比Ti-B以及Ti-Ti之间作用强烈,同时Ti原子质量比B大。结合2.3节的布局分析可知B和Ti之间离子键对光频支有重要贡献。

Figure 6. Acoustic properties of TiB2. (a) phonon dispersion spectrum; (b) phonon state density
图6. TiB2的声学性质。(a) 声子色散谱;(b) 声子态密度
表4给出中心对称点Γ点振动本征矢。在D6h点群下声子谱中心Γ点(图6中G点)震动模式可约表示为Γ9,分解为点群不可约表示后为
。由于TiB2属于具有中心对称的P6/mmm群,因此光频支中具有红外活性和Raman活性的振动模式是互补的。在上面得到的可约表示中,三个声频支振动模式可约表示为
,其中A2u是Ti和B原子沿[0 0 0 1]方向的振动,E1u是(0 0 0 1)面内的振动模式。由于
振动模式仅有B原子参与,不属于声频支,剩余的可约表示
都是光频支,B2g是B沿[0 0 0 1]方向的相对振动模式,E2g是B在(0 0 0 1)面内的相对振动模式,其余的三支是Ti和B原子都参与的过程。红外活性振动方式为
,具有Raman活性的是2E2g,B2g属于光学跃迁禁止模。

Table 4. Center symmetry points Γ vibration eigen vector
表4. 中心对称点Γ点振动本征矢
本文在2.3节提到在MgB2结构中,Mg原子面向B原子层电荷转移强化了电声耦合,对提高超导转变温度是有利的,但从目前对MB2化合物研究结论来看,除MgB2以外,其他第二主族元素,第二副族元素二硼化物超导转变温度都远远低于MgB2 [14] ,因此在对声子谱计算的基础上,我们采用简单的理论模型对TiB2的超导转变温度进行了估算,计算公式如式(2) (Equation (2))。
(2)
其中
是0 K时物质的超导态在Fermi面的带隙;
是声子平均角频率;
是Fermi面处物质的DOS强度;
是超导体电声耦合系数。
本文计算得到纵声子的平均能量为69.3 meV,根据公式(2),估算TiB2的超导转变温度接近0 K,和文献 [15] 计算数据一致。主要原因是Cooper电子对耦合强度参数
数值太小,
也是第二主族以及副族元素二硼化物中最小的(如MgB2,
,
)。因此虽然TiB2结构和MgB2类似,但基本可以忽略其超导性,甚至远远小于别的层状二硼化物。
4. 结论
1) 在Ti原子和B原子间存在电子转移并以离子键和共价键组成的混合化学键相联系。TiB2的导带和价带电子主要是Ti3d和B2p轨道的价电子构成,价电子通过离域大π键在电流的作用下可发生迁移,决定了TiB2具有良好的导电性。布局分析表明,TiB2中原子间的电荷转移类似MgB2。B的p轨道接受来自于Ti的电子。
2) 光学性质计算表明,TiB2中B原子平面内sp2杂化σ键态之间以及2pz轨道构成的离域大π键之间跃迁是一个重要的部分,同时还有能带顶部满足偶极辐射的2p-3d,2p-4s能带之间的跃迁。
3) 声子谱计算结果表明TiB2中LA(LO)和TA(TO)之间的分裂很显著,声子谱中色散关系有9条,分别为3条声频支和6条光频支,在光频支中四条属于TO,剩余两条属于LO。无论是声频支还是光频支,频率较高的部分都来自于晶体中原子间作用力强的,原子质量小的B原子。预测TiB2超导转变温度计算值约为0 K。
基金项目
本文得到国家自然科学基金(51465014)和广西科技厅(桂科合1346011-5)的支持。
参考文献
NOTES
*通讯作者。