1. 引言
缆索无损探伤的方法和仪器种类繁多,其中在实际的探伤过程中,脉冲反射式超声波探伤仪应用最为广泛 [1]。
在超声波信号的传输路径上,材料的曲线或不连续会造成声阻抗的不一致,超声波在两种不同声阻抗的交界面上将会发生反射 [2] ,根据反射信号可判断缆索是否有损伤。
鉴于实际检测过程中,回波信号的强弱和缆索内部的缺陷大小成正比,对于较大的缺陷,回波信号非常明显,可以很方便地辨识,而对于比较小的缺陷,回波信号非常微弱,甚至淹没在噪声中,无法清晰辨识。
传统的处理方法是使用放大器对采集的信号进行放大处理,但是该方法在放大信号的同时也放大了噪声,信噪比依然不大 [3]。较为先进的是基于混沌理论的微弱信号处理方法,能够较好地提取出回波信号,但是该方法处理繁琐,检测成本较高 [4]。为了在降低检测成本的同时能够有效地采集出微弱的回波信号,本文基于信号噪声在时域的分布属于正态分布的特性,通过放大、滤波和时间线叠加抵消等方式,设计了一种对缆索无损探伤微弱信号的处理方法。在放大回波信号的同时将噪音消减,有效地提高了缆索探伤信号中微弱信号的信噪比,大大提高了无损探伤的准确性。
2. 缆索无损探伤系统
缆索无损探伤系统通过在准确的时序控制下,对微弱信号进行多次采集,并将采集到的信号序列严格按照时间线累加。由于信号噪声在时域的分布属于正态分布,即均匀且对称的分布在真实值两侧,经过累加后会互相抵消;而真实信号不属于正态分布,经过多次累加,信号值会被放大;所以通过此种方法在放大噪声的情况下,有效地放大了信号,使得微弱的内部缺陷产生的微弱信号能够被清晰的分辨出来 [5] [6]。
缆索无损探伤系统主要由主MCU、时间线发生端口、信号输入/输出端口和数据输出端口组成。如图1所示。
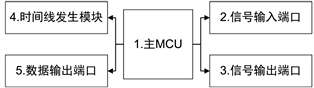
Figure 1. Hardware diagram of cable NDT system
图1. 缆索无损探伤系统硬件框图
3. 信号处理
本文缆索无损探伤微弱信号的处理方法主要是通过产生精确时间线;多次在严格的时序控制下产生信号;多次严格时序控制下的信号序列采集;时序对应信号累加;归一化等步骤,实现了不放大噪声的情况下对微弱信号进行有效的放大 [6] [7]。
根据正态分布的概率密度函数
(1)
其分布函数为:
(2)
式(1)和式(2)中,参数μ为均值;σ为均方根差。由于噪音处于正态分布,则经过M次叠加后(M值尽可能大)其值趋于ME(x)。其中
(3)
根据正态分布的原理可知
,即
 (4)
(4)
将M组数据在N个时间线采集的数值用
矩阵S表示:
(5)
将矩阵在相同的时间线采集的数数值进行叠加 [8] ,得到
(6)
然后对矩阵值进行归一化处理。取其中最小值作为权重值
,将N个时间线的值分别与权重值相减。当检测次数M趋向无穷大时,根据噪音在时域的分布属于正态分布的特性,若Th处检测的信号是噪音时,其
会趋近于0。若其中Th不为噪音,其值不遵循正态分布,随着M的增大,
的值也会增大 [9] [10]。
实验其具体实现步骤如图2所示。
1) 由图1中的4产生时间线,作为整个流程的时序基准。
2) 在T1时刻,由图1中的2产生发射脉冲信号,并等待50 ms。
3) 等时间间隔,从图1中的3采集回波信号序列,保存为
。
4) 重复2~3步骤M次,得到
~
,M组信号序列。
5) 将M组信号序列按照进行矩阵相加运算,得到结果序列。对结果序列进行归一化,得到最终结果序列数据。
6) 将结果序列通过图1中的5进行数据输出,显示成回波曲线,方便测试人员判断结果。
4. 实验结果分析
本文使用超声导波缆索检测仪分别采集了M系数为10、50、100和1000的实验信号,通过接收回波信号并对实验信号进行归一化处理后,对信号的数据结果进行对比分析。实验数据如表1所示,仿真信号图如图3~7所示。由实验数据可知,通过此种方法在不放大噪声的情况下,能够有效地放大真实信号,清晰分辨出微弱的内部缺陷引起的微弱信号,有效的提高了无损探伤的准确性。

Table 1. Signal processing results of coefficients
表1. 典型累加系数的信号处理结果

Figure 4. Processed signal with coefficient 10
图4. 累加系数为10的处理后信号
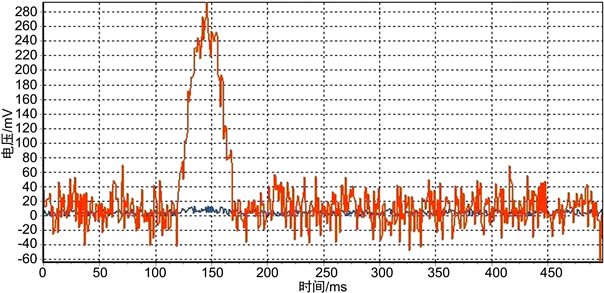
Figure 5. Processed signal with coefficient 50
图5. 累计系数为50的处理后信号
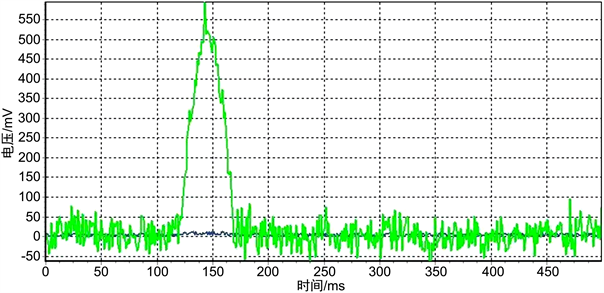
Figure 6. Processed signal with coefficient 100
图6. 累计系数为100的处理后信号

Figure 7. Processed signal with coefficient 1000
图7. 累计系数为1000的处理后信号
5. 结束语
本文提出的一种对缆索无损探伤微弱信号的处理方法,通过在准确的时序控制下,对微弱信号进行多次采集,并严格按照时间线累加,在不放大噪声的情况下,有效地放大了真实信号,提高了缆索无损探伤过程中由内部缺陷引起的微弱信号的分辨能力。该方法应用简单,容易实现;增加的额外硬件很少,对主MCU的性能要求不高;适用范围较广,针对不同检测方法的微弱信号处理亦可以被采用。
参考文献