一类混合束方法子问题的求解研究

Study on the Solution of a Hybrid Bundle Method Subproblem

摘要: 非光滑优化问题的求解一直以来都是优化理论的重点研究对象，本文提出了一类带有矩阵范数的混合束方法子问题，然后利用对偶空间理论研究该问题的Lagrange函数，最后通过对偶问题与原问题的关系，计算出该混合束方法子问题的解，并给出具体的表达式。

Abstract: The solutions of non-smooth optimization problem have been the focus of the optimization theory for a long time. This paper proposes a class of hybrid bundle method subproblem with matrix norm, and then researches this subproblem’s Lagrange function by taking advantage of the dual space theorem. Finally, based on relation between the dual problem and the original problem, the solution of hybrid bundle method subproblem is calculated, and the concrete expression is given.

1. 引言

对非光滑优化问题来说，束方法是其最有效的解决方法之一。很多学者在束方法的理论和应用方面都取得了较多的有益成果，见文献 [1] [2] [3] [4] [5] 。考虑原始问题 $\underset{x\in R^n}{\min }f\left(x\right)$ ，其中 $f$ 是 $R^n\to R$ 的非光滑凸函数。文献 [6] 中作者提出了一个带矩阵范数的双稳定子问题，文献 [7] 中作者对目标函数增加迫近项和对可行域增加信赖域约束，灵活地把邻近束方法和信赖域束方法结合起来构造了混合束方法。通过 [6] 和 [7] 的启发，本文提出了一类带矩阵范数的混合束方法子问题：

$\{\begin{array}{c}\min {\hat{f}}_k\left(x\right)+\frac{1}{2{\tau }_k}{\left|x-x^k\right|}_k^2\\ \text{s}\text{.t}\text{.}{\left|x-x^k\right|}_k^2\le {\delta }_k^2\end{array}$

这里引用了矩阵范数，并通过计算得到该子问题解的表达式。

2. 预备知识

束方法基本原理是在迭代进行到第 $k$ 步时，产生了一组候选点列 ${\left\{y^i\right\}}_{i=1}^k$ 和一组稳定中心点列 ${\left\{x^i\right\}}_{i=1}^k$ ，它利用候选点列的信息来构造目标函数 $f\left(x\right)$ 的切平面近似 ${\hat{f}}_k\left(x\right)$ ，然后求得 $d^k$ ，令 $y^{k+1}=x^k+d^k$ 作为下一个候选点，然后进行下降性检验，以此来确定下一个稳定中心，同时更新束，如此迭代得一点列 $\left\{x^k\right\}$ ，满足 $\left\{x^k\right\}$ 的任一聚点都是原问题的最优解。

束方法具体来说常见的有信赖域束方法、邻近束方法和水平束方法，其中信赖域束方法和邻近束方法的迭代格式分别为：

$\begin{array}{l}{y}^{k+1}=\arg \min \left\{{\hat{f}}_k\left(x\right)|\Vert x-x^k\Vert \le {\delta }_k,x\in R^n\right\}\\ y^{k+1}=\arg \min \left\{{\hat{f}}_k\left(x\right)+\frac{1}{2{\tau }_k}{\Vert x-x^k\Vert }^2|x\in R^n\right\}\end{array}$

其中 ${\delta }_k>0$ 为信赖域参数， ${\tau }_k>0$ 为邻近参数。

3. 混合束方法子问题的产生

受文献 [6] 和 [7] 的启发，本文提出了一类带矩阵范数的混合束方法子问题：

$\{\begin{array}{c}\min {\hat{f}}_k\left(x\right)+\frac{1}{2{\tau }_k}{\left|x-x^k\right|}_k^2\\ \text{s}\text{.t}\text{.}{\left|x-x^k\right|}_k^2\le {\delta }_k^2\end{array}$ (2.1)

在这里令 ${\hat{f}}_k\left(x\right)=\underset{j\in J^k}{\max }\left\{f\left(y^j\right)+\langle g^j,x-y^j\rangle \right\}=\underset{j\in J^k}{\max }\left\{f\left(x^k\right)+\langle g^j,x-x^k\rangle -{\alpha }_j^k\right\}$ ，其中， $f$ 在 $x^k$ 点的线性化误差为 ${\alpha }_j^k=f\left(x^k\right)-f\left(y^j\right)+\langle g^j,x-y^j\rangle$ ，由此知 $g^j\in {\partial }_{{\alpha }_j}f\left(y^j\right)$ ， $J^k$ 为指标集， $x^k$ 为当前稳定中心，当 $k\to \infty$ 时， ${\delta }_k\to 0$ ，记问题(2.1)的最优解为 $x^{k+1}$ 。我们定义原空间范数 ${|\cdot |}_k^2=\langle M_k\cdot ,\cdot \rangle$ ，其对偶空间范数为 ${\Vert \cdot \Vert }_k^2=\langle \cdot ，M_k{}^{\text{-}1}\cdot \rangle$ ， $M_k$ 是对称正定矩阵。

当迭代次数的增加，束中的元素原来越多，对之后的计算和储存会带来巨大的麻烦，所以采用现已有的聚合技术，将束进行压缩至只保留 $n{p}_k$ 个元素， $n{p}_k$ 甚至有可能小于 $k$ ，这时 $j\in \left\{1,2,\cdots \cdots ,n{p}_k\right\}$ ，接着我们对其对偶问题展开研究。

4. 混合束方法子问题解的表达式

由于问题(2.1)是非光滑凸优化问题，对非光滑凸优化问题来说在满足Slater约束规格的条件下，对问题的求解可以转化为其极小化Lagrange函数问题的求解，也就是说必然存在一个乘子 $0\le {\lambda }_k\in R$ ，能

使 $x^{k+1}=\arg {\min }_{x\in R^n}L\left(x,{\lambda }_k\right)$ ，在这里 $L\left(x,{\lambda }_k\right)：={\hat{f}}_k\left(x\right)+\frac{1}{2{\tau }_k}{\left|x-x^k\right|}_k^2+\frac{1}{2}{\lambda }_k\left({\left|x-x^k\right|}_k^2-{\delta }_k^2\right)$ ，故问题(2.1)等价于下述问题：

$\{\begin{array}{c}\min {\hat{f}}_k\left(x\right)+\frac{1}{2{\tau }_k}{\left|x-x^k\right|}_k^2+\frac{1}{2}{\lambda }_k\left({\left|x-x^k\right|}_k^2-{\delta }_k^2\right)\\ x\in R^n\end{array}$ (3.1)

问题(3.1)还可以等价的写成：

$\{\begin{array}{c}\min {\hat{f}}_k\left(x\right)+\frac{1+{\lambda }_k{\tau }_k}{2{\tau }_k}{\left|x-x^k\right|}_k^2-\frac{{\lambda }_k{\delta }_k^2}{2}\\ x\in R^n\end{array}$ (3.2)

我们定义相应的额定下降：

${\xi }_{k+1}：=f\left(x^k\right)-\left({\hat{f}}_k\left(x^{k+1}\right)+\frac{1+{\lambda }_k{\tau }_k}{2{\tau }_k}{\left|x^{k+1}-x^k\right|}_k^2-\frac{{\lambda }_k{\delta }_k^2}{2}\right)$

定理3.1：令问题(2.1)的最优解为 $x^{k+1}$ ，假设参数 ${\delta }_k,{\tau }_k>0$ ，则有

$x^{k+1}=x^k-\frac{{\tau }_k}{1+{\lambda }_k{\tau }_k}{M}_k^{-1}{\hat{g}}^k$ ，其中 ${\hat{g}}^k={\displaystyle \underset{j=1}{\overset{n{p}_k}{\sum }}\stackrel{-}{\beta }}{g}^j$

并且 $\bar{\beta }=\left({\bar{\beta }}_1，{\bar{\beta }}_2,\cdots ，{\bar{\beta }}_{n{p}_k}\right)$ 是下述问题的最优解

$\{\begin{array}{c}\min \frac{{\tau }_k}{2\left(1+{\lambda }_k{\tau }_k\right)}{\Vert {\displaystyle \underset{j=1}{\overset{n{p}_k}{\sum }}{\beta }_j}{g}^j\Vert }_k^2+{\displaystyle \underset{j=1}{\overset{n{p}_k}{\sum }}{\beta }_j}{\alpha }_j^k\\ s.t.\beta \in {\Delta }_k:=\left\{z\in {\left[0,1\right]}^{n{p}_k}:{\displaystyle \underset{j=1}{\overset{n{p}_k}{\sum }}{z}_j=1}\right\}\end{array}$ (3.3)

证明：因为问题(3.2)和问题(2.1)是等价的，所以可以通过引入变量 $r$ 得到问题(3.2)的等价形式如下：

(3.4)

当 $\beta \in R_{+}^{n{p}_k}$ 时，问题(3.4)的Lagrange函数为：

$L\left(x,r,\beta \right)=r+\frac{1+{\lambda }_k{\tau }_k}{2{\tau }_k}{\left|x-x^k\right|}_k^2-\frac{{\lambda }_k{\delta }_k^2}{2}+{\displaystyle \underset{j=1}{\overset{n{p}_k}{\sum }}{\beta }_j}\left(f\left(x^k\right)+\langle g^j,x-x^k\rangle -{\alpha }_j^k-r\right)$

整理得：

$L\left(x,r,\beta \right)=\left(1-{\displaystyle \underset{j=1}{\overset{n{p}_k}{\sum }}{\beta }_j}\right)r+{\displaystyle \underset{j=1}{\overset{n{p}_k}{\sum }}{\beta }_j}\left(f\left(x^k\right)+\langle g^j,x-x^k\rangle -{\alpha }_j^k\right)+\frac{1+{\lambda }_k{\tau }_k}{2{\tau }_k}{\left|x-x^k\right|}_k^2-\frac{{\lambda }_k{\delta }_k^2}{2}$

由于目标函数是强凸的，所以问题(2.1)有且仅有一个解。记最优乘数为 $\bar{\beta }$ ， $\left(x^{k+1},\bar{\beta }\right)$ 可以从问题(3.4)和它的对偶问题中获得。

$\underset{\left(x,r\right)\in R^n\times R}{\min }\underset{\beta \in R_{+}^{n{p}_k}}{\max }L\left(x,r,\beta \right)=\underset{\beta \in R_{+}^{n{p}_k}}{\max }\underset{\left(x,r\right)\in R^n\times R}{\min }L\left(x,r,\beta \right)$

该问题与问题(3.4)的有限最优值是一样的，不一样的是对偶问题的内层是无约束最小化优化问题，所以必有 $1-{\displaystyle \underset{j=1}{\overset{n{p}_k}{\sum }}{\beta }_j=0}$ 。基于以上结论，问题(3.2)的最优解 $x^{k+1}$ 和最优乘数 $\bar{\beta }$ 分别可以从原问题和对偶问题中得到。

$\underset{x\in R^n}{\min }\underset{\beta \in R_{+}^{n{p}_k}}{\max }L\left(x,\beta \right)=\underset{\beta \in R_{+}^{n{p}_k}}{\max }\underset{x\in R^n}{\min }L\left(x,\beta \right)$

其中

$\begin{array}{c}L\left(x,\beta \right)={\displaystyle \underset{j=1}{\overset{n{p}_k}{\sum }}{\beta }_j}\left(f\left(x^k\right)+\langle g^j,x-x^k\rangle -{\alpha }_j^k\right)+\frac{1+{\lambda }_k{\tau }_k}{2{\tau }_k}{\left|x-x^k\right|}_k^2-\frac{{\lambda }_k{\delta }_k^2}{2}\\ =f\left(x^k\right)+{\displaystyle \underset{j=1}{\overset{n{p}_k}{\sum }}\left(\langle {\beta }_j{g}^j,x-x^k\rangle -{\beta }_j{\alpha }_j^k\right)}+\frac{1+{\lambda }_k{\tau }_k}{2{\tau }_k}{\left(x-x^k\right)}^T{M}_k\left(x-x^k\right)-\frac{{\lambda }_k{\delta }_k^2}{2}\end{array}$

考虑对偶问题，对于 $\forall \beta \in {\Delta }_k$ ，应用 $x\left(\beta \right)=\arg {\min }_{x}L\left(x,\beta \right)$ 的最优性条件 ${\nabla }_{x}L\left(x\left(\beta \right),\beta \right)=0$ 。即

${\nabla }_{x}L\left(x\left(\beta \right),\beta \right)={\displaystyle \underset{j=1}{\overset{n{p}_k}{\sum }}{\beta }_j{g}^j}+\frac{1+{\lambda }_k{\tau }_k}{{\tau }_k}{M}_k\left(x\left(\beta \right)-x^k\right)=0$ (3.5)

记 ${\hat{g}}^k={\displaystyle \underset{j=1}{\overset{n{p}_k}{\sum }}\bar{\beta }}{g}^j$ ，当 $\beta =\bar{\beta }$ ， $x\left(\bar{\beta }\right)=x^{k+1}$ 时，有 $x^{k+1}=x^k-\frac{{\tau }_k}{1+{\lambda }_k{\tau }_k}{M}_k^{-1}{\hat{g}}^k$ 。

接下证明 $\bar{\beta }$ 是问题(3.3)的解。

首先，在式子(3.5)的两边同时乘 $x\left(\beta \right)-x^k$ 得

${\displaystyle \underset{j=1}{\overset{n{p}_k}{\sum }}{\beta }_j{g}^j\left(x\left(\beta \right)-x^k\right)}+\frac{1+{\lambda }_k{\tau }_k}{{\tau }_k}{\left(x\left(\beta \right)-x^k\right)}^T{M}_k\left(x\left(\beta \right)-x^k\right)=0$

即

${\displaystyle \underset{j=1}{\overset{n{p}_k}{\sum }}{\beta }_j\langle g^j,x\left(\beta \right)-x^k\rangle }+\frac{1+{\lambda }_k{\tau }_k}{{\tau }_k}{\left|x\left(\beta \right)-x^k\right|}_k^2=0$ (3.6)

同理在式(3.5)两边同时乘 $M_k^{-1}$ 得

$M_k^{-1}{\displaystyle \underset{j=1}{\overset{n{p}_k}{\sum }}{\beta }_j{g}^j}+\frac{1+{\lambda }_k{\tau }_k}{{\tau }_k}\left(x\left(\beta \right)-x^k\right)=0$ 。

再在两边同乘 $\frac{{\tau }_k}{1+{\lambda }_k{\tau }_k}{\displaystyle \underset{j=1}{\overset{n{p}_k}{\sum }}{\beta }_j{g}^j}$ 得

$\frac{{\tau }_k}{1+{\lambda }_k{\tau }_k}{\displaystyle \underset{j=1}{\overset{n{p}_k}{\sum }}{\beta }_j{g}^j}{M}_k^{-1}{\displaystyle \underset{j=1}{\overset{n{p}_k}{\sum }}{\beta }_j{g}^j}+{\displaystyle \underset{j=1}{\overset{n{p}_k}{\sum }}{\beta }_j\langle g^j,x\left(\beta \right)-x^k\rangle }=0$ 。

即

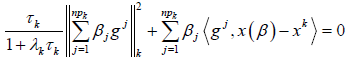(3.7)

将式子(3.6)和式子(3.7)联立，得

$\frac{{\tau }_k}{1+{\lambda }_k{\tau }_k}{\Vert {\displaystyle \underset{j=1}{\overset{n{p}_k}{\sum }}{\beta }_j{g}^j}\Vert }_k^2=\frac{1+{\lambda }_k{\tau }_k}{{\tau }_k}{\left|x\left(\beta \right)-x^k\right|}_k^2$

故有

$\begin{array}{c}L\left(x\left(\beta \right),\beta \right)=f\left(x^k\right)+{\displaystyle \underset{j=1}{\overset{n{p}_k}{\sum }}\left(\langle {\beta }_j{g}^j,x-x^k\rangle -{\beta }_j{\alpha }_j^k\right)}+\frac{1+{\lambda }_k{\tau }_k}{2{\tau }_k}{\left|x-x^k\right|}_k^2-\frac{{\lambda }_k{\delta }_k^2}{2}\\ =f\left(x^k\right)+\frac{1+{\lambda }_k{\tau }_k}{2{\tau }_k}{\left|x-x^k\right|}_k^2-\frac{{\lambda }_k{\delta }_k^2}{2}+\langle {\displaystyle \underset{j=1}{\overset{n{p}_k}{\sum }}{\beta }_j{g}^j},x-x^k\rangle -{\displaystyle \underset{j=1}{\overset{n{p}_k}{\sum }}{\beta }_j{\alpha }_j^k}\\ =f\left(x^k\right)+\frac{{\tau }_k}{2\left(1+{\lambda }_k{\tau }_k\right)}{\Vert {\displaystyle \underset{j=1}{\overset{n{p}_k}{\sum }}{\beta }_j{g}^j}\Vert }_k^2-\frac{{\lambda }_k{\delta }_k^2}{2}+\langle {\hat{g}}^k,-\frac{{\tau }_k}{1+{\lambda }_k{\tau }_k}{M}_k^{-1}{\hat{g}}^k\rangle -{\displaystyle \underset{j=1}{\overset{n{p}_k}{\sum }}{\beta }_j{\alpha }_j^k}\\ =f\left(x^k\right)+\frac{{\tau }_k}{2\left(1+{\lambda }_k{\tau }_k\right)}{\Vert {\hat{g}}^k\Vert }_k^2-\frac{{\lambda }_k{\delta }_k^2}{2}-\frac{{\tau }_k}{1+{\lambda }_k{\tau }_k}{\Vert {\hat{g}}^k\Vert }_k^2-{\displaystyle \underset{j=1}{\overset{n{p}_k}{\sum }}{\beta }_j{\alpha }_j^k}\\ =f\left(x^k\right)-\left(\frac{{\tau }_k}{2\left(1+{\lambda }_k{\tau }_k\right)}{\Vert {\hat{g}}^k\Vert }_k^2+\frac{{\lambda }_k{\delta }_k^2}{2}+{\displaystyle \underset{j=1}{\overset{n{p}_k}{\sum }}{\beta }_j{\alpha }_j^k}\right)\end{array}$

综上所述 $\bar{\beta }$ 是问题(3.3)的解。

5. 结论

本文从Lagrange对偶空间理论出发，研究了一类带有矩阵范数的混合束方法子问题，并通过计算得到该子问题的解，最后给出解的具体表达式，为以后束方法问题研究工作的展开提供了新的理论基础。