1. 引言
迄今人们依然认为,1) 光度法的理论基础是朗伯–比尔定律;2) 入射光的“非单色性”造成了光度法实际与朗伯–比尔定律的不符;3) 根据朗伯–比尔定律的微分法,断定光度法测定结果的相对误差
,最佳测定范围为1% [1] [2] [3] [4] [5];4) 为了保证测定结果可靠,在实际光度法中都采用多个标准样品绘制“校准曲线” [6] [7] [8] [9] [10];5) 每个方法的入射光都应是“吸收谱带”的峰值 [11];6) 方法的测定含量范围也必须是方法给定的。7) 测定结果的不确定度评定,只能采用“合成法”。而作者在严格遵循“精密度法则”,即“保持影响测量各因素对同一测定系列各个样品影响的一致性”条件下,却有了全然不同的新认识。现以高锰酸光度法对碳钢、高锰钢、锰铁中锰的测定为例,做详细论述。
2. 实验部分
2.1. 主要仪器与试剂
分光光度计:721型,中国上海精密仪器仪表有限公司;HCA (滤光片)分析仪:无锡市高速分析仪器厂;硝酸溶液(体积比):HNO3:H2O = 1:4;硫–磷混酸(体积比):硫酸:磷酸:水 = 1:1:2;过硫酸铵溶液(质量比):5%过硫酸铵水溶液(现用现配);硝酸银溶液(质量比):1%。10 g硝酸银溶于1000 mL蒸馏水,加20 mL硝酸;实验用水:必须为蒸馏水;实验所用试剂均为分析纯。
2.2. 实验条件
遵循“精密度法则”,即“保持影响测量各因素对同一测定系列各个样品(包括标准样品)影响的一致性”,是对光度法新认识的必要条件。影响光度法测定的有人、机、料、法、环5大因素,控制它们的一致性的具体细节分述如下。
2.2.1. 人的因素控制
同一测量系列所有样品的测量过程(如称量,溶样,定容等等)可以多人协作,但同一测定系列的同一程序(如称量或溶样等),必须由同一计量合格人员按照同一方式实施;
2.2.2. 机械因素的控制
光度法应用的机械主要有太平、器皿、光度计。同一测量系列样品的称量,必须用同一天平的同一量程、同一状态进行称量;同一测量系列的同一容量,必须用同一器皿按照同一方式实施计量;同一测量系列的吸光度测定,必须用同一比色皿在光度计的同一状态测定;
2.2.3. 物料因素的控制
光度法的物料主要是样品、化学试剂和溶剂。同一测量系列的样品、试剂必须是同一原装,溶剂必须是同一原装试剂的同一批次配制;
2.2.4. 环境因素的控制
影响光度法的环境因素主要是温度和时间。本实验显色在一定温度范围的水浴中摇动加热一定时间,然后流水冷却至室温后定容、放置,并在一定时间内完成测定。
2.3. 实验方法
2.3.1. 碳钢中锰的测定
称取样品0.2000 g置于200 mL锥形瓶中,加硝酸溶液30 mL,加热,赶去氮的氧化物。样品溶解后,流水冷却至室温,在100 mL容量瓶中加水定容,作为样品“母液”。用10 mL刻度移液管移取“母液”10 mL,置于200 mL锥形瓶中。用5 mL刻度移液管分别加入硝酸银溶液、过硫酸铵溶液各5 mL。在80℃~100℃水浴中摇动加热40 s,取出,流水冷却至室温。30 min内,用1 cm比色皿,以水作参比,520 nm处测定吸光度。
2.3.2. 高锰钢中锰的测定
称取样品0.2000 g置于200 mL锥形瓶中,如上法制备成“母液”100 mL。用10 mL刻度移液管移取“母液”10 mL,置于100 mL容量瓶中,加硝酸溶液30 mL,并加水定容,作为样品“待测液”。用10 mL刻度移液管移取“待测液”10 mL置于200 mL锥形瓶中,按照2.3.1方法显色,并测定吸光度。
2.3.3. 锰铁中锰的测定
称取样品0.2000 g置于200 mL锥形瓶中,加硫–磷混酸20 mL,加热,滴加硝酸破坏碳化物。样品溶解后,流水冷却至室温,在100 mL容量瓶中加水定容,作为样品“母液”。用2 mL刻度移液管移取“母液”2 mL于100 mL容量瓶中,加硝酸溶液30 mL,加水定容,作为样品“待测液”。用10 mL刻度移液管移取“待测液”10 mL置于200 mL锥形瓶中,按照2.3.1方法显色,并测定吸光度。
3. 结果与讨论
3.1. “化学物质吸光规律”
选择7个碳钢标准样品,其含锰量(%)分别为:0.19、0.48、0.77、0.96、1.40、1.78、2.02,在严格遵循“精密度法则”条件下,按照本文2.3.1方法测定吸光度,结果见表1。

Table 1. Absorption of manganese standard sample at 520 nm
表1. Mn标准样品520 nm的吸光度
根据表1数据绘制“校准曲线”(图1)
从图1可以看出,在入射光值域(0.11~0.86)内,所有样品的含量、吸光度的坐标点(C, A)都落在同一直线上,其方程是“两点式”:
(1)
根据图1,直线方程同样可是如下形式:
(2)
以吸光度改变量ΔA、样品含量改变量ΔC分别替代
、 ,式(2)可简化为:
,式(2)可简化为:
(3)
式(3)与A = kC不同,这正是朗伯–比尔定律与光度法实际不符的根本原因。
它表明,在严格遵循“精密度法则”条件下,“在入射光值域内,吸光度改变量ΔA与吸光物质含量的改变量ΔC成正比:
。”我们称这一规律为“化学物质吸光规律”。这一规律的存在,决定了在入射光值域内的所有样品的坐标点(C, A)都会落在同一
的直线上,所以上、下限两个标准样品的坐标点(CII, AII)、(CI, AI)连线,即是样品含量Cx的“测定线”,无需再绘制“多点校准曲线”。样品含量Cx既可根据吸光度Ax,在“正比测定线”上查找,也可通过仪器根据下式直接数字显示结果:
(4)
如:求吸光度
对应的锰含量Cx。
从“测定线”上查0.760相对应的锰含量是1.78%。仪器根据式(4)将
、
、
、
、
、
代入式(4)显示样品锰含量:
表明式(4)与“正比测定线”是等效的。
3.2. 吸收谱带内的光具有加合性
迄今,人们都认为,是入射光的非单色性导致了光度法实际与朗伯-比尔定律的不符,实际上吸收带是化学物质基态不同量子能级量子化吸收的体现,它的各个光束都可用于相关物质含量的测定。它们的非单色性不仅不会对它们测定相关物质含量产生负面影响,反而会提高它们的测定灵敏度。表2是同一高锰钢比色系列,在721分光光度计和HCA三元素分析仪同一530 nm处测得的吸光度。

Table 2. Absorption of the same series of high manganese steel at 530 nm of different photometers
表2. 同一高锰钢测定系列在不同光度计530 nm处的吸光度
表2中的数据表明,两组测定结果均服从
,但由于HCA是滤光片光度计,它的530 nm光束比721的530 nm光束宽,所以同是530 nm,但吸光度却比721高出了近一倍。表明吸收谱带内光束愈宽,测定灵敏度愈高。同时也表明光度计不应追求入射光的“单色性”,反而应当采用“非单色性”入射光,以提高它的灵敏度。
3.3. 光度法测定结果的相对误差
任何物理量的测定结果都是一个随机数,从朗伯–比尔定律的微分法,推导出光度法测定结果的相对误差的数学模型:
,是不科学的。
我们在721光度计的520 nm处,对同一碳钢锰的测定系列中,透光率T ≈ 0.695含锰0.29%和透光率T ≈ 0.174含锰1.78%的两个样品,分别实施了9次重复测定,测定结果列于表3:

Table 3. RSD of determination results of samples with different transmittance
表3. 不同透光率样品测定结果的RSD
根据相对误差数学模型,透光率愈小相对误差应愈大,但含量1.78%的透光率0.174远小于含量0.29%透光率0.695,而1.78%的相对误差RSD却仅是0.29%相对误差RSD的约1/4,充分证明,
是不符合实际的。
3.4. 光度法的测定含量上、下限
实践证明,每个光度法的测定含量上、下限,实际都是相应含量吸光度的上、下限。不同含量的样品,只要制成吸光度上、下限区间内的比色样品,即可用原方法实施测定。如碳钢锰的高锰酸光度法,测定含量上、下限的吸光度分别为0.11~0.86,要测定高锰钢、锰铁中的锰含量,就只要将它们制成吸光度处于0.11~0.86的比色样品即可。
选含锰11.14%和17.42%两个高锰钢标准样品,作为样品测定的下限和上限,按照本文2.3.2高锰钢中锰的测定方法测定吸光度。两个标准样品的吸光度分别为0.524、0.803,都在原吸光度上、下限内。所以,其上、下限两个标准样品坐标点(17.42, 0.803)和(11.14, 0.524)连线就是样品含量的“正比测定线”。从其上查找样品吸光度对应的锰含量即可,结果列于表4。
选含锰65.67%和82.09%两个标准样品,作为锰铁中锰测定的下限和上限,按照本文2.3.3锰铁中锰的测定方法测定吸光度。两个标准样品的吸光度分别为0.570、0.712,都在原方法吸光度上、下限内。其上、下限两个标准样品坐标点(65.67, 0.570)和(82.09, 0.712)连线就是样品的“正比测定线”。从其上查找样品吸光度对应的锰含量即可,结果列于表4。

Table 4. Determination results of high manganese steel and ferromanganese
表4. 高锰钢、锰铁的测定结果
高锰钢测定的允许误差为±0.20%,9次测定结果,最大误差为±0.15%。锰铁测定允许误差为±0.50%,9次测定结果,最大误差为0.40%,它们的每一次测定结果的误差都<1%,表明“光度法测定结果最佳相对误差为1%”也是不符合实际的。
3.5. 测定结果的不确定度评定
遵循“精密度法则”,同一量值μ样本的各个测得值“如出一模”。中心极限定理表明,同一量值μ的“大样本(
)”服从正态分布 [12] [13] ,“小样本”容量愈大愈近似正态分布 [13] 。“规范”之4.3.2.1指出,容量为n的“小样本”均值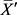 的A类标准不确定度为:
的A类标准不确定度为:
(5)
统计学指出,
是“小样本”均值
的实验标准差,它表明
落在
和
两个区间的概率分别为0.9545%和0.9973 [14] [15] 。“规范”之4.5.3表明,这两个区间的半宽度,就分别是均值
的扩展不确定度
:
,
(6)
,
(7)
S是“小样本”各测得值的实验标准偏差。“小样本”近似正态分布,所以S可按照极差法
评估。根据“规范”要求,“小样本”容量应取10,则
,
[16] 。将
代入式(2)、式(3),即可得到量值μ“小样本”均值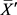 的扩展不确定度:
的扩展不确定度:
,
(8)
,
(9)
式(8)、式(9)表明,均值
的不确定度与“小样本”极差成正比,与“小样本”容量的平方根成反比,符合客观实际,具有普遍的适用性 [17] [18] 。
4. 结语
严格遵循“精密度法则”是光度法的新认识的必要条件,文中表述的“精密度法则”实施细节,是认识、应用、推广光度法的基础技术;光度法的新认识,简化了光度法的操作和不确定度的评定,并把光度法的含量测定范围扩大到了任意含量,还为光度计的研制提供了新的思路,对光度法的应用和发展都具有一定的参考价值。
参考文献