嘉陵江梯级水库运行期设计洪水及汛控水位

Design Floods and Control Water Levels of Jialing River Cascade Reservoirs in Operation Period

摘要: 论述水库建设期和运行期设计洪水、汛限水位和汛控水位的差异。采用最可能地区洪水组成法，分析计算了嘉陵江梯级水库运行期设计洪水及汛控水位。结果表明：1) 梯级水库联合调度对下游水库洪水具有一定的削减作用，草街水库运行期千年一遇的设计洪峰、3 d和7 d洪量的削减量(削减率)分别为11,457 m³/s (18%)、13.5亿m³ (12%)和11.1亿m³ (5%)；2) 在保证防洪标准不变的前提下，亭子口与草街梯级水库运行期汛控水位相比汛限水位可适当抬高，分别为447 m (447.4 m)和200 m (202.3 m)，汛期年均发电量分别增加了1.1%和4.8%，共增发电量1.1亿kW∙h/年。

Abstract: The differences between reservoir construction and operation periods, flood limited water level and flood control water level, were discussed. The most likely regional flood composition method was applied to derive and analyze design floods as well as the flood control water levels of Jialing River cascade reservoirs in operation period. Results reveal that: 1) the design floods of downstream reservoirs are moderately influenced by the operation of upstream reservoirs. The 1000-year design flood peak, 3 d, and 7 d flood volumes of Caojie Reservoir decrease by 11,456 m³/s (18%), 1.35 (12%) and 1.11 billion m³ (5%), respectively; 2) the flood control water levels of downstream reservoirs are slightly higher than flood limited water level with the same flood prevention standards. The flood control (limited) water levels of Tingzikou and Caojie Reservoirs in operation period are 447.4 (447) and 202.3 (200) m, which can increase the hydropower generation by 1.1% and 4.8%, respectively, and in total 0.11 billion KW∙h annually.

1. 引言

水利枢纽工程在规划设计阶段，根据工程的防洪标准、开发任务和规模等，采用单站天然年最大洪水系列推求设计洪水，确定水库防洪和调节库容及其特征水位。这些设计值常选用最恶劣的组合，从偏安全考虑取外包值，确保大坝和防洪安全，称为“建设期设计洪水”，并用汛期防洪限制水位(简称“汛限水位”)指导水库调度运行。

水利枢纽工程竣工验收后投入正常运行，上下游边界条件或水库功能已经发生了很大的变化，如我国大部分河流已经形成梯级水库群格局 [1] 。受上游水库的调蓄影响，水文情势相对于天然情况发生了显著变化，水库“运行期设计洪水”及特征水位、运行调度方式都应随之改变。为了不要混淆概念，用水库运行期汛期防洪控制水位(简称“汛控水位”)指导水库调度运行。

我国《水利水电工程设计洪水计算规范(SL44-2006)》 [2] (简称《规范》)中对水库建设期设计洪水的理论较为完善，但对水库运行期设计洪水理论仍为空白。在梯级水库建成的格局下，仍沿用水库建设期设计洪水及汛限水位，无法实现水库群综合利用效益最大化。因此，考虑上游水库调蓄影响，开展梯级水库运行期设计洪水及汛控水位研究，对补充完善规范、提高梯级水库群的运行管理水平，意义重大。

郭生练等 [3] 论述了水库运行期的设计洪水理论和方法，其核心是推求控制断面以上各分区洪水的地区组成。《规范》中推荐采用的同频率地区组成法应用较广泛，但该方法同频率假定的合理性要视分区和设计断面的相关性密切程度而定。相比于同频率地区组成法，最可能地区组成法具有以下优势：1) 在所有可能的地区组成方案中，其发生的可能性最大，具有较强的统计基础，避免了同频率假设的任意性；2) 其方案数唯一，不随水库数目的增加而增加，因此在梯级水库维数较高时亦能有效应用。闫宝伟等 [4] 应用Copula函数推求了上游断面与区间洪水最可能地区组成；刘章君等 [5] 利用Copula函数推导了梯级水库最可能地区组成法的计算通式，为设计洪水地区组成分析计算提供了一条新途径；熊丰等 [6] 基于t-Copula函数建立了高维情况下的联合分布，采用蒙特卡洛法和NSGA法推求了金沙江下游梯级水库的最可能组成，解决了高维情况下最可能组成的求解问题。

嘉陵江是长江上游左岸一级支流，发源于陕西省秦岭南麓，流经陕西、甘肃、四川、重庆四省市，干流全场1132 km，落差2300 m，平均比降为2.05‰，流域面积15.9万km²，占长江流域面积的9%。多年平均水资源总量698.8亿m³，水资源总量丰沛，但时空分布不均 [7] [8] 。嘉陵江干流已建成亭子口和草街2座水库，支流白龙江建成碧口和宝珠寺2座水库。图1为嘉陵江流域和梯级水库概化图，随着这些梯级水库的运行应用，下游断面的设计洪水发生了一定程度的变化。本文分析嘉陵江梯级水库的最可能组成，基于最可能地区组成法计算各水库运行期设计洪水及其汛期防洪控制水位。

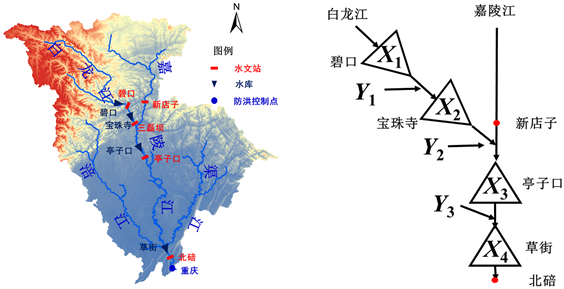
Figure 1. Sketch map of cascade reservoirs and the Jialing River basin

图1. 嘉陵江流域和梯级水库概化图

2. 最可能地区组成法

碧口–宝珠寺–亭子口–草街梯级水库天然来水分别用X₁、X₂、X₃、X₄表示，取值依次为x₁、x₂、x₃、x₄；碧–宝区间、新–宝–亭区间和亭–草区间来水分别用Y₁、Y₂、Y₃表示，取值依次为y₁、y₂、y₃。以草街水库的最可能组成为例，其不同洪水组合发生的相对可能性大小，可以用X₁、X₂、X₃、X₄的联合概率密度函数值 $f\left(x_1,x_2,x_3,x_4\right)$ 的大小来度量。 $f\left(x_1,x_2,x_3,x_4\right)$ 越大，表明该地区组成发生的可能性越大。欲得到最可能地区组成，即为求解 $f\left(x_1,x_2,x_3,x_4\right)$ 在满足水量平衡约束下的最大值，即

$\begin{array}{l}\max f\left(x_1,x_2,x_3,x_4\right)=c\left(u_1,u_2,u_3,u_4\right){\displaystyle \underset{i=1}{\overset{4}{\prod }}{f}_{X_i}\left(x_i\right)}\\ \begin{array}{cc}\text{s}\text{.t}\text{.}& \begin{array}{l}{x}_1+y_1=x_2\\ x_1+y_1+y_2=x_3\\ x_1+y_1+y_2+y_3=x_4\end{array}\end{array}\end{array}\}$ (1)

式中： $c\left(u_1,u_2,u_3,u_4\right)$ 为Copula的概率密度函数； $u_{\text{1}},u_{\text{2}},u_{\text{3}},u_{\text{4}}$ 为 $x_{\text{1}},x_{\text{2}},x_{\text{3}},x_{\text{4}}$ 的经验频率。 $f_{X_i}$ 为X_i (i = 1,2, 3, 4)的概率密度函数。

采用t-Copula函数来建立各分区的联合分布。t-Copula分布函数的表达式为：

$C\left(u;\Sigma ,v\right)={\displaystyle {\int }_{-\infty }^{{\Phi }^{-1}\left(u_1\right)}\cdots }{\displaystyle {\int }_{-\infty }^{{\Phi }^{-1}\left(u_4\right)}\frac{\Gamma \left(\frac{v+4}{v}\right)}{\Gamma \left(\frac{v}{2}\sqrt{{\left(\pi v\right)}^4\left|\Sigma \right|}\right)}{\left(1+\frac{1}{v}{\omega }^{\text{T}}{\Sigma }^{-1}\omega \right)}^{\frac{v+4}{2}}\text{d}\omega }$ (2)

式中： $\Sigma$ 为相关性矩阵， $\omega$ 为被积函数变量矩阵。

采用遗传算法(GA)求解最可能组成，主要步骤如下：

1) 根据样本确定各分区的边缘分布和联合分布。

2) 考虑水量平衡约束，以最小化联合概率密度函数的负值为目标函数进行优化求解：

$\begin{array}{l}\begin{array}{cc}\min & -\end{array}f\left(x_1,x_2,x_3,x_4\right)=-c\left(u_1,u_2,u_3,u_4\right){\displaystyle \underset{i=1}{\overset{4}{\prod }}{f}_{X_i}\left(x_i\right)}\\ \begin{array}{cc}\text{s}\text{.t}\text{.}& \begin{array}{l}{x}_1+y_1=x_2\\ x_1+y_1+y_2=x_3\\ x_1+y_1+y_2+y_3=x_4=z\end{array}\end{array}\end{array}\}$ (3)

其中优化变量为各分区的频率组合，即 $\left[u_{\text{1}},u_{\text{2}},u_{\text{3}},u_4\right]$ 。

3) 由求解得到的最优频率组合及各分区的边缘分布推求最可能地区组成。

3. 实例研究

四座水库的集水面积和设计洪水特征值如表1所示。为考虑上游水库的调蓄作用对下游水库设计洪水的影响，除采用最可能地区组成外，还与《规范》推荐采用的同频率地区组成法进行了比较。分析计算了受调蓄影响的各座水库运行期的设计洪水和汛限水位，并与建设期成果进行了对比。

Table 1. List of design flood characteristic values of cascade reservoirs in the Jialing River

表1. 嘉陵江梯级水库设计洪水特征值

3.1. 各分区洪水的边缘分布

根据嘉陵江流域的洪水特性，选取3 d、7 d作为设计洪水地区组成的控制时段。文中表格展示以7 d为控制时段的计算结果。文中的洪水地区组成计算及分析对比需得到各水库的天然洪量及洪峰设计值。采用北碚站、亭子口站、新店子站、三磊坝站、碧口站的天然洪水资料序列进行计算。频率分析采用皮尔逊三型(P3)分布和适线法，并采用K-S检验法对其进行假设检验。各水库天然设计洪水成果如表2所示。取K-S检验显著性水平为α = 0.05，p值大于0.05时通过检验。结果表明，表中的各个随机变量的P3分布均通过了K-S假设检验。

Table 2. Estimated parameters of marginal distributions for each sub-basin

表2. 各分区天然设计洪水成果

3.2. 各分区洪水的联合分布

采用t-Copula函数建立各分区3 d、7 d年最大洪量的联合分布。参数估计方法采用极大似然法，假设检验方法采用Cramer Von Mises法。取检验显著性水平为α = 0.05，p值大于0.05时通过检验。根据均方根误差RMSE和赤池信息准则AIC对t-Copula的自由度进行优选。以草街以上各分区7 d洪量联合分布的构建为例，分析结果如表3所示。由表中可见，不同自由度的t-Copula函数建立的联合分布均能通过假设检验。比较可知，自由度为3的t-Copula有着最小的RMSE和AIC值，因此选择自由度为3的t-Copula函数。t-Copula函数拟合得到的经验和理论联合分布的P-P图如图2所示，可以看出点据基本位于等值线附近，表明其能够很好的模拟实例中各分区3 d、7 d洪量的联合分布。

Table 3. Goodness-of-fit of estimated t-Copula

表3. t-Copula函数拟合结果

Figure 2. The P-P plots fitted by the joint distributions of 3 d and 7 d annual maximum flood volumes of composed sub-basins

图2. 各分区3 d和7 d年最大洪量联合分布拟合的P-P图

3.3. 洪水地区组成和梯级水库调蓄影响

得到各分区的边缘分布和联合分布后，可以求解受调蓄影响的各个水库的最可能地区组成。以草街水库为例，分析了其地区组成结果及上游水库调蓄对其设计洪水的影响。采用NSGA法求解不同频率3 d、7 d洪量的地区组成，其中7 d洪量的地区组成结果列于表4。此外，采用《规范》推荐的同频率地区组成方案I (即碧口、宝珠寺、新店子和亭子口与草街同频率，而各个区间按水量平衡原则分别发生相应洪水)作对比分析，其计算结果也列于表4。从表中可见，最可能地区组成法计算得到的不同频率的碧口、新店子洪量均小于同频率组成结果，而计算得到的新–宝–亭区间、亭–草区间洪量均大于同频率组成结果。碧–宝区间因集水面积小且不在暴雨区，两种方法计算得到的结果差异不大。总的来说，最可能地区组成结果较为合理。

Table 4. Results of most likely and equivalent frequency composition at Caojie Reservoir/(108 m3)

表4. 草街水库最可能和同频率洪水地区组成结果/亿m³

求得草街水库3 d、7 d洪量的地区组成结果后，可以计算碧口–宝珠寺–亭子口梯级水库联合调度影响下的草街水库的设计洪峰流量。以碧口、碧–宝区间、宝–亭区间和亭–草区间分配到的3 d、7 d相应洪量为控制，按1981年典型洪水过程线同频率放大得到各分区的设计洪水过程线，输入到梯级水库系统进行调洪演算。河道洪水演算采用马斯京根法。为了比较分析梯级水库的削峰作用，假定建设期的草街水库的年最大洪峰流量与3 d、7 d洪量设计频率相同。不同地区组成方案推求的受上游梯级水库影响的洪峰流量见表5。

Table 5. Comparison of design peak discharges regulated by upper cascade reservoirs at Caojie Reservoir/(m3∙s−1)

表5. 梯级水库调蓄影响的草街水库洪峰流量对比/(m³∙s⁻¹)

由表5可知，碧口–宝珠寺–亭子口梯级水库的联合调度对草街水库有较显著的削峰作用。当设计频率较高时，削峰作用更为明显，两种地区组成法计算推求的草街水库断面千年一遇设计洪水的削峰率均高于18%。另一方面，同频率方法计算得到的不同频率的削峰率均高于最可能组成法，表明最可能组成法的设计成果相对于同频率I法对防洪较为不利。

3.4. 梯级水库运行期设计洪水

由前述分析可知，上游水库的调蓄作用对下游水库的设计洪水产生了影响。现由最可能地区组成法得到宝珠寺、亭子口、草街水库各自的洪水地区组成，并由调洪演算得到各水库运行期千年一遇的设计洪峰、3 d、7 d洪量，计算结果列于表6。由表6可见：1) 宝珠寺受到碧口水库的调蓄影响较小，原因在于碧口水库的防洪库容较小，对洪水的调蓄能力不强；2) 亭子口和草街水库运行期的千年一遇洪峰流量、3 d和7 d洪量均有一定削减。草街水库受调蓄影响较显著，其运行期千年一遇的设计洪峰、3 d和7 d洪量的削减量(削减率)分别为11,457 m³/s (18%)、13.51亿m³ (12%)和11.12亿m³ (5%)。草街水库运行期千年一遇设计洪水过程线绘于图3，可以看出受上游梯级水库的调蓄影响，其设计洪水过程变得平缓。

维持各水库建设期的防洪标准不变，调洪演算得到各水库运行期汛期防洪控制水位。由表6可知，下游水库受上游水库调蓄影响，其水库运行期汛控水位要高于建设期汛限水位。亭子口和草街水库运行期汛控水位(建设期汛限水位)分别为447 m (447.4 m)、200 m (202.3 m)。表6还给出各水库按建设期汛限水位与运行期汛控水位计算得到的汛期多年平均发电量，亭子口、草街梯级水库运行期年均发电量分别增加了1.1%和4.8%，共增发电量1.1亿kW∙h/年。

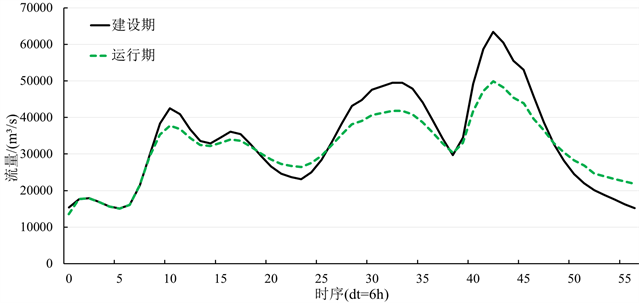
Figure 3. Comparison of 1000-year design flood hydrographs between construction and operation periods of Caojie Reservoir

图3. 草街水库建设期和运行期千年一遇设计洪水过程线比较

4. 结论

1) 最可能地区组成结果合理可信，能够为洪水地区组成的分析计算提供参考；

2) 梯级水库联合调度对下游洪水具有一定的削减作用，草街水库运行期千年一遇的设计洪峰、3 d和7 d洪量的削减量(削减率)分别为11,457 m³/s (18%)、13.51亿m³ (12%)和11.12亿m³ (5%)；

3) 在保证防洪标准不变的前提下，亭子口与草街梯级水库运行期汛控水位相比汛限水位可适当抬高，分别为447 m (447.4 m)和200 m (202.3 m)，年均发电量分别增加了1.1%和4.8%，共增发电量1.1亿kW∙h/年；

4) 若预测到流域超标准洪水或发生一些特殊紧急情况，则按建设期汛限水位指导水库调度运行。

Table 6. Comparison of 1000-year design flood values between construction and operation periods

表6. 梯级水库建设期和运行期千年一遇设计洪水特征值及削减率

基金项目

国家自然科学基金(51879192)，国家重点研发计划(2018YFC1508001)资助项目。

参考文献