计及风沙磨损的架空输电线路冰风荷载失效概率评估方法

Failure Probability Assessment Method for Overhead Transmission Lines under Ice and Wind Loads considering Blowing Sand Wear

摘要: 新疆地区输电走廊所处气候环境恶劣，导线经历风沙磨损后会导致强度损失，尤其在冰冻天气下，导线覆冰后加上大风激励容易发生线路结构失效，研究计及风沙磨损的线路冰风荷载失效概率评估方法具有重要意义。本文根据微气象监测装置，基于覆冰厚度预测模型计算冰荷载，然后依据强度干涉理论，通过对冰风组合荷载与风沙磨损后导线剩余强度进行比较，动态评估输电线路的失效概率。最后通过新疆地区某实际案例的反演分析，对所提方法的可行性和有效性进行验证。研究有助于运行人员及时校核输电线路运行状态，防范因导线覆冰和大风导致的故障。

Abstract: The transmission corridor in Xinjiang is exposed to a severe climate; the strength of the overhead line will be lost after being subjected to blowing sand wear. Especially in the freezing weather, the wind excitation plus icing is prone to structural failure of the overhead line. It is of great significance to study the failure probability evaluation method of the overhead line under ice and wind loads considering blowing sand wear. In this paper, the ice load is calculated according to the ice thickness prediction model based on the micro-meteorological monitoring devices. Then, according to the strength interference theory, the failure probability of the transmission line is dynamically evaluated by comparing the residual strength of the transmission line after blowing sand wear and the ice and wind combination loads. Finally, the feasibility and effectiveness of the proposed method are verified through the inversion analysis of an actual case in Xinjiang. The research results are helpful to check the operation status of the transmission line timely and prevent the failure caused by the line icing and strong wind.

1. 引言

近年来，全球气候异常变化 [1]，飓风、冰灾、暴雪、地震等灾害天气频频发生，特别是我国新疆地区，输电走廊常年处于低温和大风沙环境中，风沙磨损会加速导线强度损失 [2]，再加上覆冰过重和脱冰跳跃产生的附加荷载 [3]，极易导致输电线路结构失效，造成线路故障停运 [4]，影响正常送电，给国民经济和群众生活带来不利影响 [5]。因此，研究计及风沙磨损的架空输电线路冰风荷载失效概率评估方法，具有重要的理论意义和工程价值。

1998年美国、加拿大发生严重冰灾，加拿大东南部和魁北克南部省份的受灾情况最为严重，造成了28人死亡，470万加拿大人和50万美国人遭受停电影响 [6] [7]；2008年，我国南方大范围遭遇了严重的持续低温雨雪冰冻灾害天气，大范围雨雪冰冻天气影响了我国19个省区，造成大范围倒塔、断线和闪络事故，贵州、湖南、江西和浙江省电网受损最为严重 [8]。2018年1~2月，中国华南和华东地区普遍出现大面积的积雪冰冻天气，输电线路再次面临考验 [9]。

进行冰、风环境下的线路荷载计算，需要依赖于覆冰监测数据，现有覆冰监测技术主要包括拉力、倾角监测装置 [10] [11]、基于图像的覆冰在线监测系统 [12] [13] 等，这些基于直接观测或监测覆冰的装置，布点密度低，受环境及供电电源的影响，可靠性也不够高，因此监测数据可用率不佳。由于覆冰过程与局部微气象关系密切 [14] [15] [16]，导线覆冰增长受风速、覆冰时间、降水量、水滴直径、湿度和温度等因素的影响 [17] [18] [19]，导线覆冰的自动脱落同样需要一定的气象条件 [14]，因此，利用沿输电线路分布安装的微气象监测装置采集的气象数据进行覆冰厚度估计具有可行性。

对于输电线路因气象灾害失效，部分学者从风荷载 [20] 和冰荷载等荷载作用下考虑线路结构失效，其中，风荷载常会导致导线微风振动、风偏放电等 [21]，大风作用下甚至会发生断线、倒塌等严重事故 [22]；冰荷载常导致跳头、扭转、舞动、冰闪跳闸甚至断线、倒塔等恶性事故 [23]；相较于冰荷载和风荷载单独作用时，冰风组合荷载引起的输电线路结构失效风险更为严重 [24]。已有研究通常忽略风沙磨损对输电线路强度的影响，而风沙磨损将导致线路强度损失 [25]，冰风荷载作用下线路将面临更严重的事故风险 [26]，尤其是对于风沙较为严重的我国新疆等地区。然而，目前国内外对风沙冲蚀导线的机理尚不明确，对于输电线路由于风沙磨损造成的结构失效研究不足，绝大部分研究都是基于经验和实验拟合，缺乏工程基础。因此，依据历史风沙数据估计线路强度损失，对于更为客观地评估输电线路失效概率是很有必要的。

本文基于新疆地区输电线路沿线的微气象监测数据和风沙记录，分析风沙磨损对架空输电线路结构强度的影响，通过作者先前建立的覆冰厚度预测模型，进行覆冰预测，进而计算覆冰和脱冰跳跃情况下线路的失效概率，最后通过新疆地区某实际案例的反演分析，对所提方法的可行性和有效性进行了验证。本文方法有助于电网运行人员及时校核输电线路运行状态，防范因导线覆冰和大风导致的故障。

2. 基于微气象监测的输电线路冰风荷载预测

2.1. 输电线路冰厚预测

由于输电线路覆冰增长的物理机理复杂，在实际运行情况下，对于不同型号的导线、不同的地理气象环境，导线覆冰增长情况也复杂多变。本文作者在之前的研究工作 [27] 中提出了计及气象因素时间累积效应的输电线路覆冰预测方法，如图1所示。

Figure 1. Flowchart of conductor ice thickness prediction basedon micrometeorological monitoring data

图1. 基于微气象监测的导线覆冰厚度预测流程图

该方法首先根据利于形成覆冰的气温、湿度、风速、风向条件，判定导线覆冰气象等级R_tm,j(t)；然后依据覆冰厚度的平方随时间近似线性增长的关系，构建了覆冰厚度增长程度指标；进一步考虑气象因素对覆冰增长的加剧影响，对覆冰厚度增长程度指标进行线性扩展，得到了计及气象因素累积效应的覆冰厚度增长程度指标A_vtm(t)；再根据历史上覆冰厚度监测数据，采取SVM回归方法进行训练得到预测模型；最后，输入微气象监测数据和天气预报数据，便可预测当前时段及未来短时的覆冰厚度值，用于导线冰荷载计算。

本文使用文献 [14] 提供的监测数据作为模型的训练数据及测试数据，同时采用传统SVM方法对采样点气象数据及覆冰厚度数据进行训练与测试，对比本文模型预测结果，检验本文模型的有效性及精确性。文献 [14] 提供了34组覆冰数据，包括覆冰厚度、温度、湿度与风速等，采样间隔为1 h，见图3。本文使用前28组数据训练模型，利用后6组数据检验三种回归模型的预测效果。

输入后6组测试数据，计算得到测试数据的计及气象因素覆冰厚度增长程度 $A_{\text{vtm},\text{test}}\left(t\right)$ ，将其带入模型 $I\left(t\right)=f\left(A_{\text{vtm}}\left(t\right)\right)$ ，计算得到覆冰厚度的预测值，见表1所示。同时将测试数据输入BP神经网络及传统SVM方法的训练模型，并将其预测结果与本文预测结果放在表1中进行对比。从表1中可以看出，本文所提出的计及气象因素时间累积效应的覆冰预测模型的6个预测值相同，这是因为所计算的 $A_{\text{vtm},\text{test}}\left(t\right)$ 中各元素均为14。与其他各方法相比较，本文方法的阶段性、层次性更强。

Table 1. The icing forecast results

表1. 覆冰预测结果

为了更直观地对比三种方法的预测误差，图2汇总了2种方法预测值绝对误差。从图2中可以明显看出，在6个测试时间点，本文方法预测误差绝对值基本上小于传统SVM的预测结果。对比结果表明本文提出的覆冰预测模型思路是有效的。

Figure 2. Absolute errors of 2 forecasting models

图2. 2种方案预测绝对误差对比

2.2. 输电线路冰风组合荷载

计算导线上覆冰重量的方法有多种，覆冰质量m_ice可按照D. G. Havard [28] 推荐的公式计算：

$m_{\text{ice}}=0.5\text{π}{\rho }_{\text{ice}}\Delta r\cdot r_{\text{ice}}$ (1)

式中，r_ice的计算公式见式(2)。

$r_{{}^{\text{ice}}}=0.5\Delta r+0.25\text{π}d$ (2)

式中，r_ice为覆冰块质心到截面中心的距离；ρ_ice为冰的密度；∆r为覆冰的厚度；d为导线的半径。

当风向与导线垂直时，覆冰时的风压载荷集度为

$q_m=\frac{9.8ac\left(d+2\Delta r\right)v^2}{16}$ (3)

式中，c为风载体系数，一般情况下，导线覆冰时c可取1.2；a为风速不均匀系数；v为设计风速；d为导线的计算半径；∆r为覆冰厚度。

风荷载的计算中，还应考虑风速的不均匀性，风的不均匀性与风速大小有关，因此风荷载计算中需要考虑风速的不均匀系数a，具体的数据见表2。

Table 2. Wind speed unevenness coefficient table

表2. 风速不均匀系数表

对于线路脱冰跳跃荷载变化，可根据脱冰前后输电线路单位长度重量进行计算，如式(4)所示。

$H-H_0=\frac{EA{l}^2}{24}\left(\frac{q^2}{H^2}-\frac{q_0^2}{H_0^2}\right)$ (4)

式中，l为输电线路的长度；q₀、q分别为脱冰前后导线单位长度的重量；H₀、H分别为脱冰前后导线的张力；E为输电线的弹性模量；A为导线的横截面积。

3. 风沙磨损导致的强度损失

对于风沙磨损导致的强度损失，有学者分别从风速、风向、砂砾大小和角度、砂砾持续时间和线路荷载大小等方面进行了研究 [29]。通过新疆地区实际测量可以发现，线路强度随荷载的增大而减小，无沙磨损区域线路强度剩余率高于砂砾磨损区域20%左右，并且无沙磨损和砂砾磨损具有相同的强度剩余率下降趋势，开始阶段强度下降较快，随着时间的增加，强度下降趋于平缓，最终因强度较低，将会导致线路因强度不足发生线路失效故障。

通过对新疆地区历史监测数据进行拟合，含有砂砾磨损时线路挂接金具的强度剩余率随连续磨损时间变化的拟合公式如式(5)所示。

$W_{\text{sand}}=0.4585t^2-11.6t+114.4$ (5)

无沙磨损时，剩余强度拟合公式如(6)所示。

$W=0.2712t^2-7.257t+107.9$ (6)

式中，t为连续磨损的时间，10⁵ s。

因单次沙尘天气的持续时间较短(约几小时)，因此实际评估时可依据线路投运或更换导线金具后所经历的风沙累积时间精细剩余强度估算。

4. 输电线路冰风荷载失效概率评估

4.1. 失效概率模型

根据结构可靠性的强度干涉理论 [30]，输电线强度累积概率密度分布和荷载累积概率密度分布之间的关系如图3所示，图中f_G(g)表示输电线路永久荷载累积概率密度函数曲线，f_R(r)表示不计强度损失时的输电线路强度累积概率密度函数曲线，f_S(t)(S)表示t时刻永久荷载叠加环境荷载后的荷载累积概率密度函数曲线，f_R(t)(r)表示计及t时刻的强度损失之后的导线强度累积概率密度函数曲线。

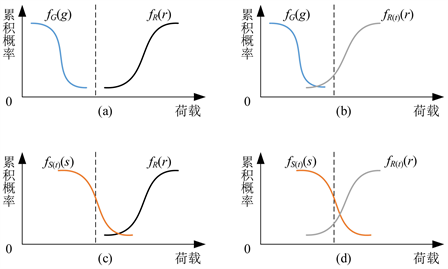
Figure 3. Interferogram of strength and loadcumulative probability density curves of overhead lines

图3. 输电线路结构强度与荷载的累积概率密度曲线干涉示意图

其中，图3(a)表示在没有冰、风等环境荷载，不计导线强度损失时，输电线路在正常服役期间，因导线的设计强度大于永久荷载，在结构上是可靠的。图3(b)表示经受长期的风沙磨损后导线的强度有所损失，强度累积概率密度曲线左移变形，使得强度和荷载累积概率密度曲线有交叉，其重叠区域称为干涉区，干涉区域的存在表明经历长时间的风沙磨损后导线强度退化，即使当前时刻没有冰、风等环境荷载，导致实际强度低于设计强度，会发生结构失效，导致输电线路故障。图3(c)表示不考虑风沙磨损导致的强度损失，因为冰、风等环境荷载增加，荷载累积概率密度曲线右移变形，导致输电线所承受的总荷载变大，当其大于导线的设计强度后，存在结构失效的可能。图3(d)表示综合考虑风沙磨损和环境荷载，干涉区域较(b)和(c)更大，发生结构失效的概率也更大。

因此，经受了风沙微振磨损后的导线，在冰风环境荷载冲击作用下，当输电线路的设计强度大于其所承受的荷载时，输电线路正常运行；反之，输电线路将发生结构失效而故障停运。因此输电线路的结构功能函数可表示为

$Z\left(t\right)=g\left(R\left(t_1\right),S\left(t_2\right)\right)=R\left(t_1\right)-S\left(t_2\right)$ (7)

式中，R(t₁)表示导线强度在风沙磨损期t₁ (亦称为退化期，为年或季节时间尺度)内的随机变化过程；S(t₂)为恶劣天气持续期间t₂ (小时级的时间尺度)导线荷载的随机变化过程。根据强度干涉理论，输电线路结构失效概率等于导线强度小于承受其所受荷载的概率，可用式(8)表示。

$P_f\left(t_1,t_2\right)=P\left(Z\left(t_1,t_2\right)<0\right)=P\left(R\left(t_1\right)-S\left(t_2\right)<0\right)$ (8)

由于线路强度R(t₁)和荷载S(t₂)是相互独立的，两者的联合概率分布为

$f_{R\left(t_1\right),S\left(t_2\right)}\left(r,s\right)=f_{R\left(t_1\right)}\left(r\right)\cdot f_{S\left(t_2\right)}\left(s\right)$ (9)

那么，将式(9)并入式(8)，可得

$\begin{array}{c}{p}_f\left(t_1,t_2\right)=p\left(R\left(t_1\right)<S\left(t_2\right)\right)\\ ={\displaystyle \iint f_{R\left(t_1\right)}}\left(r\right)\cdot f_{S\left(t_2\right)}\left(s\right)\text{d}r\text{d}s\\ ={\displaystyle \underset{0}{\overset{+\infty }{\int }}{f}_{S\left(t_2\right)}\left(s\right)F_{R\left(t_2\right)}\left(s\right)\text{d}s}\end{array}$ (10)

由IEC60826标准可知，一般情况下，荷载和强度均服从高斯分布，联合概率密度函数为

$f_{Z\left(t_1,t_2\right)}=\frac{1}{\sqrt{2\text{π}}{\sigma }_Z}\exp \left(-\frac{{\left(z-{\mu }_{Z\left(t_1,t_2\right)}\right)}^2}{2{\sigma }_Z^2}\right)$ (11)

式中， ${\mu }_{Z\left(t_1,t_2\right)}={\mu }_{R\left(t_1\right)}-{\mu }_{S\left(t_2\right)}$ ； ${\sigma }_Z^2={\sigma }_R^2+{\sigma }_S^2$ ； ${\mu }_{R\left(t_1\right)}$ 、 ${\mu }_{S\left(t_2\right)}$ 分别为强度和荷载概率密度函数的均值； ${\sigma }_R$ 、 ${\sigma }_S$ 分别为强度和荷载概率密度函数的标准差； ${\mu }_{Z\left(t_1,t_2\right)}$ 、 ${\sigma }_Z$ 分别为联合概率密度函数的均值和标准差。

因此，式(10)可以表示为

$$ (12)

令

$\alpha \left(t_1,t_2\right)=\frac{z\left(t_1,t_2\right)-{\mu }_{Z\left(t_1,t_2\right)}}{{\sigma }_Z}$ (13)

则可将式(12)变换为标准正态分布

$p_f\left(t_1,t_2\right)=p\left(Z\left(t_1,t_2\right)<0\right)={\displaystyle \underset{-\infty }{\overset{-\frac{{\mu }_{z\left(t_1,t_2\right)}}{{\sigma }_Z}}{\int }}\frac{1}{\sqrt{2\text{π}}}\exp \left(-\frac{{\alpha }^2\left(t_1,t_2\right)}{2}\right)\text{d}\alpha }$ (14)

所以在输电线路的结构失效概率为

$p_f\left(t_1,t_2\right)=\Phi \left(-\frac{{\mu }_{z\left(t_1,t_2\right)}}{{\sigma }_Z}\right)$ (15)

上述计算过程求解的是一段档距的失效概率，对于处在同一气象区域内的一整条输电线，假设具有n档，那么整条输电线路的失效概率相当于n段线路失效的串联，如图4所示。

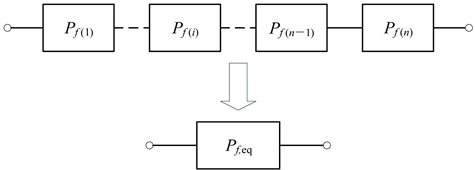
Figure 4. Series equvilent modeloftransmission line failure probability

图4. 输电线路失效概率的串联等效模型

图4中， $P_{f\left(i\right)}$ 为第i段线路的失效概率， $P_{f\left(n\right)}$ 为第n段线路的失效概率， $P_{f,\text{eq}}$ 为n段线路串联后的等效失效概率，根据串联网络的定义可以求得一整条输电线的失效概率，如式(16)所示。

$P_{f,\text{eq}}\left(t\right)=1-{\displaystyle \underset{i=1}{\overset{n}{\prod }}\left(1-P_{f\left(i\right)}\right)}$ (16)

4.2. 评估流程

对于风沙磨损后，输电线路覆冰及脱冰跳跃失效概率可根据图5所示流程进行评估。首先依据先前提出的覆冰增长模型，根据微气象监测装置所测气象参数，计算覆冰厚度，结合历史数据，对输电线路结构强度进行评估，判断其强度损失，在覆冰重量不足以导致线路故障时，继续校核脱冰跳跃失效概率，当失效概率大于所设阈值时，及时提醒运行调度人员，保证电网的安全稳定运行。

Figure 5. Flowchart of transmission line failure probability evaluation

图5. 输电线路失效概率评估流程

5. 算例分析

新疆电网某输电线路在2015年11月22日16:49~19:58因导线覆冰及脱冰跳跃接连发生5次跳闸，为此，采用该线路在2015年11月21日~23日逐10 min的微气象监测数据进行反演测试，其气象数据如图6和图7所示。

Figure 6. Ambient temperature and humidity data acquired by a micrometeorological monitoring equipment

图6. 某微气象监测装置采集的气温和相对湿度数据

Figure 7. Wind speed and wind direction data acquired by a micrometeorological monitoring equipment

图7. 某微气象监测装置采集的风速和数据

该输电线路所用导线型号为LGJK-310/50，其参数如表3所示。

Table 3. Conductor parameters of LGJK-310/50

表3. LGJK-310/50导线参数

依据微气象监测数据和历史风沙记录，该输电线路因风沙磨损导致的强度损失如图8所示。

Figure 8. Comparison of wind-sand wear strength loss

图8. 风沙磨损强度损失对比图

从图8可以看出，经过长时间的风沙磨损，导线强度较无沙磨损时强度降低20%左右，因此在导线覆冰时，输电线路承载能力进一步降低，应及时关注覆冰厚度，避免因覆冰过重或脱冰跳跃导致的断线断股事故，保证电网稳定运行。

根据所提覆冰预测模型及冰风荷载下输电线路失效概率预测方法，该条线路覆冰厚度预测值和对应失效概率如图9所示。

Figure 9. Ice thickness and failure probability prediction

图9. 覆冰厚度及失效概率预测图

该输电通道跳闸记录显示，故障段线路在2015年11月22日16:49至当日19:58间接连发生5次跳闸，时间对应图中的时间序号为152~171。从预测输出结果可以看出，输电线路先经历气象累积作用，然后冰厚逐渐增长，在线路发生实际跳闸之前(时间序号为115~125)，导线覆冰估计值已达到15~19 mm，失效概率大于0.6，此时运行人员应及时采取措施，防范因冰风荷载过大或后续脱冰跳跃造成的故障。当气温逐渐回升(时间序号为132~162)，该覆冰段冰厚将减小，但在风的激励下将会发生脱冰跳跃，失效概率大于0.7，预测结果与实际记录相符，验证所提模型的有效性。当气温再次下降时，部分未脱冰线路覆冰厚度将会进一步增大，对于线路承载力和结构强度又会产生很大考验，应及时采取措施，保证电网的安全运行。

6. 结语

输电线路长时间经受风沙磨损会导致输电线路强度下降，在冬季冰冻天气下，导线覆冰外加大风将影响线路安全运行，冰风组合荷载作用下线路失效概率增大，应及时校核线路强度。本文依据先前所提覆冰增长模型，根据实时微气象监测数据进行覆冰增长及脱冰跳跃发展趋势的动态估计，进而在综合考虑线路风沙磨损强度损失情况下，进一步进行失效概率评估，所得结果有助于电网运维决策，及时发出风险预警，采取除冰和融冰措施，保证输电线路安全运行。