1. 引言
高压直流输电技术是解决远距离大容量电能输送、可再生能源并网以及多个不同频率的交流系统互联问题的有效手段之一,其发展经历了从常规直流输电、常规多端直流输电到柔性直流输电、柔性多端直流输电再到直流电网的历程 [1] 。目前柔性多端直流输电技术已较为成熟,全球已有多个工程建成投运,包括中国的南澳三端柔性直流输电工程、舟山柔性五端直流输电科技示范工程以及美国的Tres Amigas超导体输电工程等 [2] 。随着研究深入,“换流站少,工程造价低、可灵活切换传输方式且运行可靠性高”的直流电网受到越来越多国内外学者的关注。目前针对直流电网的研究才刚刚开始,未来逐渐成熟的直流电网将与交流电网逐步实现互联,形成交直流联合电网这一新型网络架构 [3] 。换流器是连接直流电网与交流电网的关键设备。文献 [4] [5] [6] 从不同角度分析了电流源换流器(CSC)与电压源换流器(VSC)的运行特性,比较了二者的技术特点和应用领域,指出VSC可实现有功、无功独立解耦控制,控制方式更加灵活且无需额外的无功功率补偿及通信联络设备建设,满足无源网络、远距离孤立负荷、海上钻井平台等特殊场合供电需求,较之CSC更适用于实现交、直流电网互联。
直流电压是联合电网运行稳定性的重要指标,其控制方式中应用较为广泛的是主从控制和电压下垂控制。文献 [7] [8] [9] 对交直流联合电网直流侧电压的控制方式进行了研究。文献 [7] 结合两种控制方式的优点修正了P-V曲线,解决了控制模式切换过程中暂态时间过长的问题。文献 [8] 认为现有的电压下垂控制方式未考虑扰动后直流网络功率重新分配给交流网络带来的影响,提出了一种适用于VSC-HVDC的改进电压下垂控制方法,该方法依据交流网络频率偏移自动调节响应换流站的电压下垂系数,从而合理分配扰动带来的功率不平衡量。文献 [9] 提出电压下垂系数设置不合理会导致系统失稳,可通过实时监测直流侧电压动态修正电压下垂系数,从而保证系统安全稳定运行。目前国内外学者对电压下垂控制的改进大多是围绕协调优化下垂系数展开,对下垂控制的其它参数(如:参考电压、参考功率)的优化研究还很少。本文旨在将这些可控参数与系统网损联系起来,探究这些参数对直流电压和系统网损的影响。
2. 交直流联合电网网损计算模型
网损是系统运行经济性的重要指标。交直流联合电网网损如式(1)所示。
(1)
式中:
表示联合电网总网络损耗;
分别表示交流、直流线路有功损耗及VSC换流器总损耗,其具体计算公式如下:
(2)
式中:
分别表示交、直流线路数目以及VSC换流器个数;
表示第k条交流线路的电导;
分别表示第k直流线路的电流、电阻;
表示第i个VSC换流器损耗,根据文献 [10] [11] [12] 可知,VSC换流器损耗可表示为关于电流标幺值的二次函数形式,其系数
表示换流器损耗系数,应由VSC出厂参数及实际工况来设定。
3. 交直流联合电网直流电压控制方式
3.1. 直流电压控制方式分类
直流侧电压控制方式可分为主从控制、电压裕度控制和电压下垂控制。在主从控制中,一般选择一个容量较大的换流站作为主换流站,主站采用定直流电压控制,其余从站采用定有功功率控制,一旦系统内出现功率波动则由主站承担这部分功率差额,若主站故障或超出主站可承担范围,则依靠通信系统发出指令,指定某一从站接替主站维持系统内功率平衡。电压裕度控制是对主从控制的改进,一旦主站发生故障,从站能够自动转换控制模式接替主站维持系统电压稳定。在电压下垂控制中,多个换流站工作在电压下垂控制方式下,一旦系统内出现功率波动就由这部分换流站依据各自的电压下垂系数来分担功率差额。由于电压下垂控制相比主从控制和电压裕度控制具有更多的换流站参与维持系统功率平衡,其系统运行可靠性更高且换流站之间不依赖通信系统,能够依据各自的电压下垂系数自动切换工作点,因此更适用于交直流联合电网。
3.2. 电压下垂控制原理
在直流电网中,直流线路上的电压损耗很小,可近似认为直流网络各节点电压相等。电压下垂控制原理可以用P-V特性曲线来描述,如图1所示。
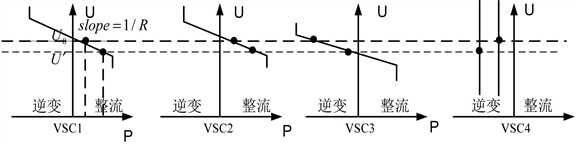
Figure 1. Principle of voltage droop control
图1. 电压下垂控制原理
由图1可知,VSC1、VSC2、VSC3采用电压下垂控制,其电压或功率不再恒定不变而是满足以下线性关系:
(3)
式中:
表示换流器实际输出功率;
表示换流器节点实际电压;
均为VSC换流器可控参数,分别表示VSC换流器下垂控制的参考功率,参考电压及电压下垂系数。对单个换流站而言,参考功率,参考电压确定了P-V特性曲线的参考运行点,电压下垂系数确定了P-V特性曲线斜率,这三个参数共同决定了该换流站的运行特性。调节换流站三个可控参数中的任意一个即可调节换流站输出功率,本文旨在分析三个可控参数对联合电网网损的影响,从中选出调节灵敏度高且能保证系统稳定运行的优化参数,将其作为电压下垂控制方式下交直流联合电网无功优化的首选优化参数。
VSC4采用定功率控制,当VSC4出现功率波动时,换流站的工作电压均由 变为
,VSC1、VSC2、VSC3会沿着各自的P-V特性曲线寻找新的工作点,从而使系统重新回到功率平衡。多个换流站共同承担维持系统功率平衡的任务,增加了系统的运行可靠性。
变为
,VSC1、VSC2、VSC3会沿着各自的P-V特性曲线寻找新的工作点,从而使系统重新回到功率平衡。多个换流站共同承担维持系统功率平衡的任务,增加了系统的运行可靠性。
3.3. 电压下垂控制下的直流电网模型
直流电网参数简单,其基本模型可以描述为:
(4)
式中:
分别表示直流节点i的电压、电流和有功功率;
表示直流网络电导矩阵的元素。VSC换流器采用电压下垂控制,其直流电网模型也应做出相应的调整,直流网络基本方程式(4)可依据公式(3)修改为:
(5)
4. 算例分析
4.1. 仿真条件
本文选取数值鲁棒性强,对初值选取不敏感的原对偶内点法 [13] [14] [15] 对算例系统进行求解。交流网络由IEEE14和IEEE4节点交流系统修改而来,三个海上风电场分别通过VSC1,VSC2,VSC3与直流电网相连,同时直流网络通过VSC4,VSC5,CSC6与交流网络实现互联。VSC1~VSC4均采用定有功功率控制,其控制量分别为
;VSC5、VSC6均采用电压下垂控制,VSC其它参数:
,
,
;VSC损耗系数均取:a = 0.01,b = 0.03,c = 0.01。交流系统发电机组出力可调,调节范围参见表1,为探究VSC5、VSC6不同下垂控制参数对系统网损的影响,进行四组仿真实验,实验参数对比详见表2,算例系统拓扑结构如图2所示。

Figure 2. Topology of the example system
图2. 算例系统拓扑结构

Table 1. Constraints on generator output
表1. 发电机组出力约束

Table 2. Comparison of droop control parameters of VSC5 and VSC6 in four groups of experiments
表2. 四组实验的VSC5、VSC6下垂控制参数对比
4.2. 仿真结果分析
为探究VSC下垂控制不同参数对系统网损的影响,设置以下三种不同场景进行对比分析。
场景1:探究VSC参考功率对系统网损的影响。设置对照组和实验组1进行对比试验,对照组的所有参数随机给定,实验组1的电压下垂系数和参考电压给定,参考功率可调,其调节范围均为−2.0 pu至2.0 pu,对比两组实验系统网损计算结果。
场景2:探究VSC参考电压对系统网损的影响。设置对照组和实验组2进行对比试验,对照组的所有参数均给定,实验组2的电压下垂系数和参考功率给定,参考电压可调,其调节范围均为−1.96 pu至2.03 pu,对比两组实验系统网损计算结果。
场景3:探究VSC电压下垂系数对系统网损的影响。设置对照组和实验组3进行对比试验,对照组的所有参数均给定,实验组VSC4、VSC5的电压下垂系数和参考功率给定,参考功率可调,其调节范围均为0.5至70,对比两组实验系统网损计算结果。
1) 直流电压对比
在调节VSC电压下垂参数的过程中,一旦直流电压随功率波动过大就很可能会造成系统失稳,因此要将系统运行的稳定性放在首位,保证在调优过程中直流电压波动不大。四组实验直流电压对比如图3所示。

Figure 3. DC voltage comparison before and after optimization of scenes 1, 2 and 3
图3. 场景1、2、3优化前后直流电压对比
对比对照组和实验组1数据可知,VSC5、VSC6的参考功率优化后,仅VSC5、VSC6对应节点电压波动较明显,其余节点直流电压基本不变;对比对照组和实验组2数据可知,VSC5、VSC6的参考电压优化后,所有节点的直流电压均发生不同程度的波动,直流电网电压波动较大;对比对照组和实验组3数据可知,VSC5、VSC6的电压下垂系数优化前后所有节点直流电压基本不变。
从系统运行稳定性的角度分析,调节电压下垂系数对直流电压的影响最小,调节参考功率次之,调节参考电压会使整个直流电网电压发生比较大的波动。
2) 系统网损优化效果对比
VSC不同参数的网损优化效果如表3所示,由图表数据可知,优化VSC5、VSC6下垂控制参考功率或参考电压,其输出功率发生显著变化,系统网损也大大降低;而对换流器电压下垂系数来说,即使将其调至最优也不能使换流器输出功率发生明显变化,系统网损优化效果不佳。

Table 3. Comparison of network loss optimization effects of different parameters of VSC
表3. VSC不同参数的网损优化效果对比
从系统运行经济性的角度分析,优化电压下垂控制参考功率和参考电压比优化电压下垂系数的网损降低效果更好。
5. 结论
从系统运行可靠性的角度分析,调节VSC电压下垂系数对直流电压的影响最小,但同时由于电压下垂系数对VSC输出功率的调节能力有限,调节VSC电压下垂系数并不能使系统网损明显减少。
从系统运行经济性的角度分析,调节VSC参考电压的网损优化效果最好,但同时调节参考电压会使整个直流网络电压发生较大的波动,甚至可能造成系统失稳。
综合系统运行可靠性和经济性两方面的要求,考虑将VSC下垂控制参考功率作为首选的优化参数。调节VSC参考功率能够在保证系统安全稳定运行的同时,使系统网络损耗大大降低,是一种有效的无功优化措施。