1. 引言
近年来,复杂网络正处于蓬勃发展的阶段,成为一个能很好地描述社会科学,自然科学,数理学科,生命学科和工程技术等领域相互关联的复杂模型。一个典型的网络由许多节点与连接节点之间的边组成,节点代表系统中的个体,边则表示节点间的作用关系。数学、计算机以及各个研究领域的基础内容等都是复杂网络的分析工具,自组织,自相似,小世界,无标度等是复杂网络的特性,复杂系统则是复杂网络的研究目标。随着对网络性质的一些相关研究,人们发现了很多实际网络都拥有一个共同特性,即社团结构。复杂网络中社团结构的特性为:社团内部各个节点的连边相对比较紧密,而社团之间相互连接的边比较稀疏。现如今,研究人员已经提出了很多有关复杂网络划分的方法,这些方法为各个领域的研究人员提供了强有力的工具。无论从实际意义还是从理论研究的角度看,研究网络的社团结构都很重要,理由如下:可以从网络结构上更好地理解节点与边的联系和功能;可以以社团为基本单位从中去探究整个网络的动态性;可以揭示网络的层次结构,并有助于理解网络;可以为真实世界中规模庞大的稀疏数据提供一种研究方法。通过对于复杂网络的划分从而揭示了网络中社团结构的特性,不仅有助于了解网络的拓扑结构,而且具有很强的实际应用价值 [1] [2] 。
谱平分法 [1] [3] [4] [5] 是复杂网络社团结构划分的一种有效算法,在部分网络社团划分中存在错误识别的现象,针对谱平分法错误识别的问题,本文在谱平分法的基础上,提出了基于节点重要度评价函数和社团划分相结合的一种算法。通过对实际网络和人工网络的划分证实了算法的可行性和有效性,得到了较好地划分结果,对复杂网络中社团划分的研究具有重要的参考意义。
2. 基础理论及相关概念
定义1 [1] 一个图是由点集
以及V中元素无序对的一个集合
所构成的二元组,记为
,V中的元素
称为节点,E中元素
称为边。
定义2 [1] 对于非赋权图
,
,构造一个矩阵
,其中
,
称矩阵A为非赋权图G的邻接矩阵。
定义3 [1] 设网络具有N节点。则节点
的度指标定义为
,
式中:
为与节点
直接相连的节点的数目,即节点
的度。
定义4 [1] 在具有N个节点的无向网络中一个节点的度不会超过
,故归一化的度指标定义为
。
定义5 [1] 设G是无向连通网络,网络节点数为N,
为网络G的邻接矩阵,D表示对角线为
的对角矩阵,定义网络G的Laplace [6] (拉普拉斯)矩阵(也称为Kirchhoff矩阵)为
。
谱平分法的理论基础是在一个有N个节点的无向网络G中,网络的Laplace矩阵是对称矩阵
,
的对角线上的元素
是节点
的度,其他非对角线上的元素
则表示节点
和节点
的
连接关系:如果这两个节点之间有边的连接,则
,否则为0。矩阵
有一个最小的特征值为0,且其对应的特征向量为
。可以从理论上证明,非零特征值所对应特征向量的各个元素中,同一个社团内节点的对应元素是近似相等的 [1] [2] 。
假设矩阵
是一个对称矩阵,矩阵
的n个特征值为
且
,其对应的n个特征向量为
且
,其中
为0,
为全等向量,第二小特征值
对应的特征向量为
,又被称作Fiedler向量 [7] 。根据网络Laplace矩阵第二小的特征值
将其分为两个社团,这是谱平分法的基本思想。当网络近似地分成两个社团时,用谱平分法可以得到非常好的划分结果,但是,当网络不满足这个条件时,谱平分法的优点就不能充分的得以体现 [8] 。
3. 基于节点重要度的社团划分方法
度是网络单个节点属性中简单且很重要的内容。从图中或邻接矩阵中,可以明显看出一个节点的度越大,即在该网络中就越“重要” [9] 。仅仅用度指标去衡量网络中节点的重要性显然比较片面,因此本文考虑邻居节点对所研究节点重要性的影响。这样网络中节点自身的重要程度和邻居对其重要性影响程度共同衡量该节点的重要度。本文定义节点重要度评价函数,如下所示:
设在一个无权无向无自环的网络中,定义一个节点重要度评价函数为
;
其中:节点
的度为
,那么节点
自身的度指标为
,
,
表示节点
对节点
的重要度影响力;
表示网络中节点
到节点
的最短距离。
空间自相关理论提出这样一个观点,两个事物所处的距离越远,那么彼此间依赖性就越弱,鉴于此,本文认为,如果网络中任意两个节点间的距离越远,那么就说明这两个节点彼此之间的影响力越低,反之,彼此间的影响力越高。现在大部分研究人员也认为有连边的节点之间会具有一些关系,即节点在复杂网络中的重要性不能只用单一的指标去刻画,需要从不同的角度,利用多种属性进行较好的评价。
重要节点在一个网络中占有很显著的地位,找到重要节点不仅有助于分析网络的结构,而且可以更好地发现整个网络中隐藏的一些规律。利用节点的重要度对复杂网络中社团的划分也同样是复杂网络研究领域的重点。在这样的一个思路下,故本文所提出的节点重要度评价函数是节点自身的度值与其邻居节点对其重要度影响力的一个差值,本文算法便是基于此函数引出的。这个函数不仅包含节点自身的属性,也包含邻居节点对节点重要度的影响力,从而进一步对节点的重要度进行评价。随后结合谱平分法的思想,计算节点重要度评价函数的最小特征值及所对应的特征向量,根据第二小特征值所对应特征向量的正负可将复杂网络中的社团进行划分。算法的具体描述如下:
对于一个无向无权含有n个节点的网络
,基于谱平分法划分复杂网络社团结构的算法的基本步骤如下:
1) 输入具有n个节点的复杂网络
。写出网络的邻接矩阵并将邻接矩阵初始化,输入邻接矩阵的上角矩阵;
2) 计算节点
的自身的度指标
;随后计算节点
对节点
的重要度影响值
;最后输出节点重要度评价函数
所形成的矩阵;
3) 求此矩阵的最小的两个特征值及特征值所对应的特征向量,根据元素的正负便可将网络划分成两个社团。特征向量中所有的正的元素对应的网络节点所形成的属于同一个社团,其他负的元素对应的节点属于第二个社团;
4) 根据以上步骤,可以将网络进行划分,刷新图形便可得出划分后的图形。
为了更清楚的表达本文算法的思想和有效性,选取一个构建好的小网络(见图1)进行验证。首先输入网络的邻接矩阵,然后计算出每个节点的度指标(如表1)及其邻居节点对它的重要度影响值,随后输出节点重要度评价函数矩阵,最后计算此矩阵中最小特征值所对应的特征向量(如表2),根据特征向量的正负进行对网络的划分。

Figure 1. 8 points of undirected network
图1. 8个点的无向网络

Table 1. Degree indicators of the corresponding nodes
表1. 对应节点的度指标

Table 2. Feature vectors for corresponding nodes
表2. 对应节点的特征向量
根据本文定义的节点重要度评价函数,算出节点重要度评价函数矩阵对应的值(如表3),进一步求得节点重要度评价函数矩阵的特征值及特征向量,那么特征向量2的正负便可将网络划分为两个社团,得到最后的划分结果(如图2)。

Table 3. Importance evaluation function values for corresponding nodes
表3. 对应节点的重要度评价函数值
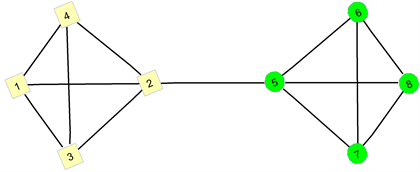
Figure 2. Results of the division of 8 points of undirected networks
图2. 8个点的无向网络的划分结果
针对上述步骤,便可将给出的示例网络正确划分。从表1的数据得知节点2和5的重要度值相等且远远大于剩余节点1,3,4,6,7,8。而节点1,3,4,6,7,8的重要度值是相等的。如果去掉节点2和5,会使网络的结构发生较大变化,对整个网络产生一定的影响。由表2和图2给出的结果可以看出,节点1,2,3,4从节点重要度评价函数矩阵得出的特征向量2的元素都为正值,即节点1,2,3,4是属于同一个社团的,图2的划分结果表明节点1,2,3,4的形状,颜色分别是正方形和米色。而节点5,6,7,8从节点重要度评价函数矩阵得出的特征向量2的元素为负值,即节点5,6,7,8是属于另外一个社团,图2的划分结果节点5,6,7,8的形状,颜色分别是圆形和绿色。即图2是8个节点无向网络的正确划分结果。
4. 实验结果与分析
Zachary空手道俱乐部网络是复杂网络 [10] 等相关领域的典型测试网络的数据集。在20世纪70年代初期,社会学家Zachary耗时两年的时间来研究美国一所大学中空手道俱乐部里34名成员之间的社会关系的网络,基于这些成员在俱乐部内外部的交往情况,构造了成员之间的社会网络体系。此网络包含34个节点和78条边,节点代表俱乐部的成员,两个节点之间有一条边则意味着相应的两个成员间至少是有交往关系的朋友。他通过观察发现,是因为俱乐部中的主管JohnA (node1)和教练员Mr. Hi (node34)之间因为是否提高俱乐部收费问题产生了一些矛盾和分歧,因此俱乐部便被分裂成分别以主管和教练为代表的两个团体。
图3中,节点1和节点34分别代表了俱乐部中的主管和教练员,而正方形和圆形的节点分别代表了分裂后的小俱乐部的各个成员。

Figure 3. Karate club network membership network
图3. 空手道俱乐部网络成员关系网络
本文算法首先输入空手道俱乐部网络的邻接矩阵,通过计算对应节点的度指标(表4)和邻居节点对其的重要度影响值,然后输出重要度评价函数矩阵,最后算出两个最小特征值及对应的特征向量(表5),根据特征向量的正负对空手道俱乐部网络进行划分。由划分的结果可以看出来本文算法划分的结果(表6)与现实中的划分结果是一致的。图4为本文算法分析空手道俱乐部网络得到的结果,共同正方形节点和圆形节点代表了原空手道俱乐部网络的实际划分分裂的结果,而米色和绿色则代表了利用本文算法得到的结果,与实际结果完全一致,达到了百分之百的正确率。图5是谱平分算法对空手道俱乐部网络得到的划分结果,从图中得知节点3被错误归类,正确率只达到了97%。所以本文算法进一步提高了谱平分法的准确率,克服了节点3错误识别的缺陷,因此本文算法更加适合对空手道俱乐部网络进行划分。

Table 4. Degree indicators of each node of the karate club network
表4. 空手道俱乐部网络各节点的度指标

Table 5. Feature vectors of corresponding nodes in karate club network
表5. 空手道俱乐部网络对应节点的特征向量

Table 6. Division of each node of the karate club network
表6. 空手道俱乐部网络节点划分情况
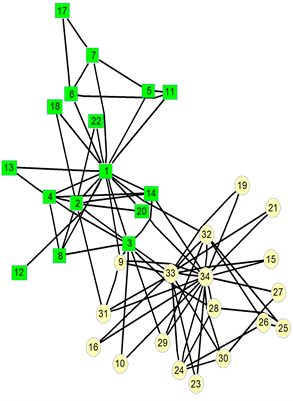
Figure 4. The results of the algorithm’s division of the karate club network
图4. 本文算法对空手道俱乐部网络的划分结果
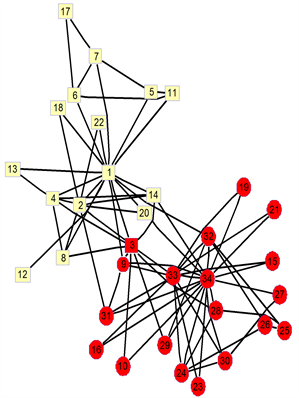
Figure 5. Results of the division of the karate club network by spectral equalization
图5. 谱平分法对空手道俱乐部网络的划分结果
5. 结束语
本文结合了谱平分法的思想,计算出了复杂网络各节点自身的度指标和邻居节点对其的重要度影响,从而构造出一个节点重要度评价函数,然后利用此评价函数的矩阵算得两个最小的特征值及其对应的特征向量,提出了一种新的复杂网络社团划分的算法。在构造的8个节点的无向网络和经典的Zachary空手道俱乐部网络上得以正确的验证,证明了该算法在复杂网络社团划分中具有可行性和有效性,通过与经典的谱平分法进行对比后,本文算法能较好的克服空手道俱乐部网络中个别节点错误识别的现象。本文算法最大的缺陷就是此算法每次只能将网络平分为两个小社团,对于将一个网络划分为两个以上社团的情况,就必须多次的进行重复运算。此算法对社团结构明显的网络划分很有效果,对社团结构不是很明显的网络,就不能得到很好地效果,所以这也是本人日后学习研究需要改进的方面。
基金项目
国家自然科学基金(11261033),内蒙古自治区高等学校科学研究项目NJZY19005。
NOTES
*通讯作者。