1. 引言
嗓音是由喉内多种物理机制相互复杂作用产生,来自肺部的气流驱动声带作周期性地张弛运动,以此构成初始的声学信号,随后经过声道传播和口腔辐射形成语音。从物理角度看,人类发声的整个过程是喉部气流、声门下系统、弹性声带和声道之间的流体–结构–声学相互作用的产物 [1]。根据嗓音的发声机理,语音的产生源于声带振动,而作用在声带表面的空气压力又是驱动声带振动的源动力,无论是正常语音还是病理嗓音实际上都被看作是通过声门的三维气流产生的。因此声门管内流场的研究有助于理解人类言语交流的系统构成,丰富对言语障碍者的临床诊断与治疗手段。
由于在分析发声过程中难以获取活体喉部区域,研究人员建立了很多实验模型和数值模型用于研究空气动力学、声带振动和声音产生。从Ishizaka和Flanagan [2] 提出声带振动的二质量块模型以来,改进的多质量块模型被广泛地应用于发声研究中 [3] [4] [5]。其主要思想是将声带组织分成小部分的质量,然后通过弹簧将相邻的质量进行耦合,以此模拟声带振动过程,虽然能够很好地表征声带振动,但是忽视了由肺部产生的动态激励源对发声的作用。数值模型运用有限体积的方法对Navier-Stokes控制方程进行离散化求解,能够将肺部气流与声带振动之间联系起来。以往对声门管内流场的研究中,数值模型可分为动态声带模型和静态声带模型。动态声带模型方面,Alipour [6] [7] 通过改变声门形状使声带产生自激振荡,研究了声带振动过程中气流流速、压力分布和气流分离点位置;Zheng [8] 等人通过改变声门间隙的宽度,研究了雷诺数和声门出口角度在发声时对声门管内射流偏转的影响。利用静态喉部模型对声门管内流场的研究奠定了语音空气动力学理解的基础 [9],并且由于其简单易行,应用更为广泛。Scherer研究组建立了声带的静态模型,从声带形状和假声带的角度对声门管内发声过程中的气体流速、声门内压进行了分析比较。通过改变模型的尺寸,如声门中部平面的横向和纵向位置 [10] [11]、声门出口半径 [12]、声门出入口倾角 [13] 等参量,实现对声带尺寸的精确控制,改变假声带间隙 [14],探究声带发声过程中不同声门尺寸和假声带的存在对声门内压力和跨声门压等影响。根据Titze [15] 推导的发声阈值压力表达式
,其中T是声带长度,D是声门直径,声带长度对发声阈值压力具有重要作用,也是影响声门管内压力速度场的其中一个重要因素。
本文在以上研究的基础上,建立声带的静态数值模型,求解声门管内流场控制方程得出其压力场分布情况,探究不同声带长度对声带表面压力分布的影响。结果表明,声带长度的增加更有利于声带振动,印证了Titze提出的发声阈值压力与声带长度的关系。
2. 声带建模与边界条件
2.1. 声带几何模型
声带模型如图1所示,由于其对称性只建立一半声带模型。本实验将声带长度定义为从声门入口到声门出口的长度,设置了三种不同长度,分别为0.108 cm、0.308 cm、0.908 cm,图1表示的长度为0.308 cm。第一种长度值(0.108 cm)用于表征轻柔声音或者高音调,而第三种长度值(0.908 cm)则用来表征相对较大声带或低音调。此外,对于上述三种声带长度,分别设置5种声门直径和3种声门下压力。声门直径数值为0.01 cm、0.02 cm、0.04 cm、0.08 cm和0.16 cm,声门下压为500 Pa,1000 Pa,1500 Pa (1000 Pa = 10.2 cm H2O)。其它固定参数值为声门入口半径Rin (0.15 cm)、声门出口半径Rout (0.108 cm)、声门入口偏转角(相对于气管方向53˚)、声门出口偏转角(相对于垂直方向90˚)、入口计算域长度(0.2 cm)、出口计算域长度(0.5 cm)、前后声门长度(1.2 cm)。
2.2. 网格划分与边界条件
利用前处理器Gambit对声门管内流体区域进行网格划分,根据物理模型自动离散生成有限元网格模型如图2所示。为了满足声带表面压力变化的精度要求,对声带表面的网格进行了加密处理。声门管内的流体是气体,其密度为1.25 kg/m3,黏度为1.7894 NS/m3。采用压力入口,分别设置为500 Pa、1000 Pa、1500 Pa,出口施加一个大气压。入口边界的湍流参数选为湍流强度I和水力直径DH。采用SIPMLE算法耦合求解,以压力入口的数值作为计算的初始条件,残差收敛精度设置为10−5,初始化后,计算迭代次数设为1000次。
3. 声门管流场分析基本理论
流体在运动过程中,遵循机械运动普遍适用的规律:质量守恒、动量守恒、能量守恒。考虑到本模型雷诺数较低(一般不大于2000),可认为气流均质、无重力、且其流动为定常、不可压缩,其求解的控制方程为连续性方程和Navier-Stokes方程。本文研究的气流运动为湍流运动,在求解气流控制方程时,由于湍流运动具有多尺度的特点,采用雷诺平均模拟方法将Navior-Stokes方程中的瞬时变量分解成平均量和脉动量进行求解,但这种方法会造成湍流基本方程不封闭,需要引入湍流模型构成封闭方程组。根据Suh J. 和Frankel S. H. [16] 对声门管采用不同湍流模型效果的比较,湍流模型选用SSTk-ω (Shear-Stress Transport)模型。该湍流模型与控制方程构成封闭求解方程组。
3.1. 连续性方程
任何流动问题都必须满足质量守恒定律。根据物质质量守恒定律可得到流体的连续性方程:
(1)
其中
为密度,t为时间,
,
,
分别为速度在x,y,z三个方向上的分量。本模型中流体不可压,其
,式(1)变为:
(2)
3.2. Navier-Stokes方程
流体系统还应满足动量守恒定律,Navier-Stokes方程是牛顿第二定律应用于牛顿粘性流体流动中的表达式。当流体为均质且不可压缩,在忽略重力的情况下,直角坐标系的Navier-Stokes方程如式(3)所示:
(3)
其中
,
,
分别为x,y,z方向上的速度分量,
是空气密度,p是空气压力,
为空气的分子黏度系数。
3.3. SST k-ω模型方程
剪切应力输送(Shear-Stress Transport,简称SST) k-ω湍流模型是由Menter于1994年提出的,该模型将k-e湍流模型与k-ω湍流模型通过混合函数结合起来,综合了k-e模型在远场计算和k-ω模型在近壁区计算的优点,并包含修正的湍流粘性公式来解决湍流剪切力引起的输运效果,从而使SST k-ω湍流模型在流动领域中有更高的精度。SST k-ω湍流模型方程如式(4)所示:
(4)
其中
为空气密度,p为压强,
、
、
为速度u、湍动能k及比耗散率
的有效扩散系数,
、
为k、
的耗散项,
为交叉扩散项,
、
、
为各输送方程的自定义原项。
4. 实验结果与分析
不同声带长度对应的声带表面压力分布的仿真结果如图3所示。(a)、(b)、(c)、(d)、(e)组图分别对应声门直径0.01 cm、0.02 cm、0.04 cm、0.08 cm和0.16 cm的条件,每组图内包括三种不同声带长度(0.108 cm、0.308 cm、0.908 cm),分别为i、ii、iii,此外,每种条件下均设置三种不同声门下压力(500 Pa、1000 Pa、1500 Pa)。
由图3声带表面压力分布图可知:不同的声带长度会影响声门管内压力场分布,从而对发声阈值压力产生作用。首先,由肺部产生的气流(预设的跨声门压力初始条件)在到达声门入口前,流场内压力不发生变化,一直保持到声门入口处;其次,当气流进入声门管时,随着声门横截面积的减少,压力突然下降(图3上横坐标为0的位置),这与流体力学中的理论相符,即气流流过管道的横截面积突然减小,会使压力突然减小,同时也由于声带壁面的黏滞效应和气流加速作用造成压力下降;最后,在声门出口处,压力恢复到外部大气压值。从图上可以看出,对于最短的声门管长度0.108 cm,这种压力变化规律更为显著。而对于声带长度0.308 cm和0.908 cm,在较大声门直径条件下,气流在从声门入口到出口的运动过程中,声带表面的压力几乎保持不变。
三种不同声带长度在不同声门直径和跨声门压的条件下,位于声门入口处(图3中轴向距离为0的位置)的压力下降值,见表1~3所示。

Table 1. Vocal cord length of 0.108 cm
表1. 声带长度为0.108 cm

Table 2. Vocal cord length of 0.308 cm
表2. 声带长度为0.308 cm
 (i)
(i)  (ii)
(ii) 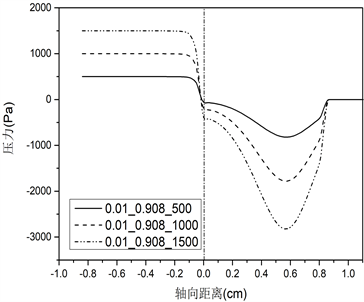 (iii) (a)
(iii) (a)  (i)
(i) 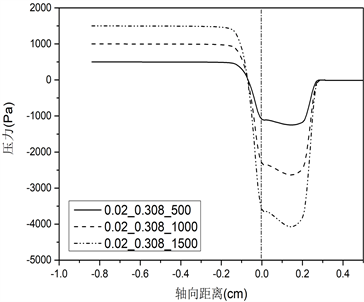 (ii)
(ii)  (iii) (b)
(iii) (b) 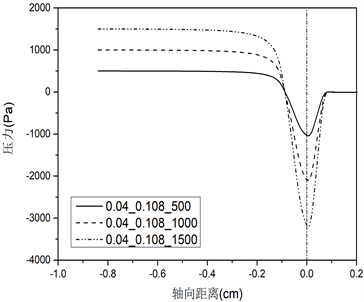 (i)
(i) 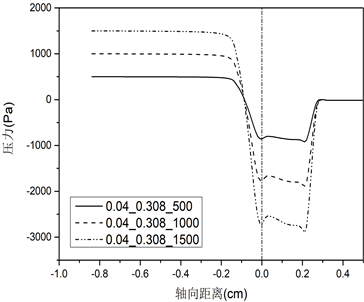 (ii)
(ii) 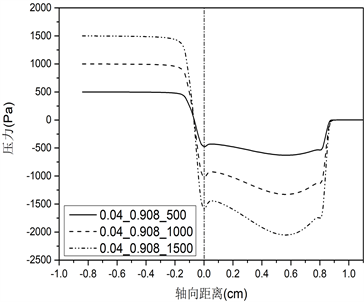 (iii) (c)
(iii) (c)  (i)
(i) 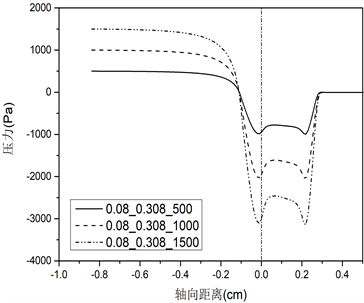 (ii)
(ii) 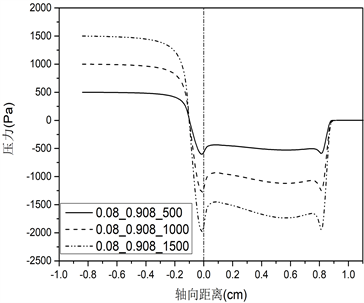 (iii) (d)
(iii) (d) 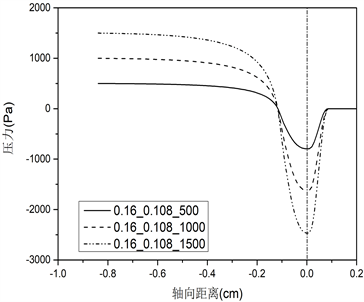 (i)
(i) 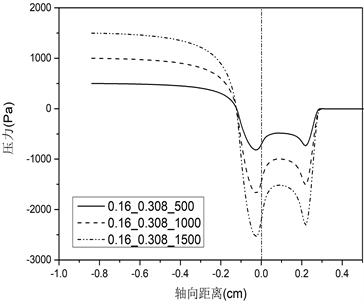 (ii)
(ii) 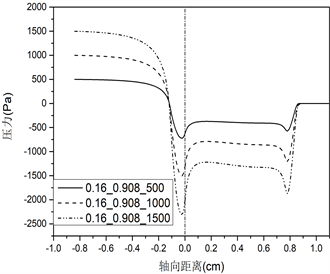 (iii)(e)
(iii)(e)
Figure 3. Surface pressure distribution of vocal cords corresponding to different vocal cords lengths. (a) 0.01 cm and (b) 0.02 cm, (i) 0.108 cm, (ii) 0.308 cm, (iii) 0.908 cm; (c) 0.04 cm and (d) 0.08 cm, (i) 0.108 cm, (ii) 0.308 cm, (iii) 0.908 cm; (e) 0.16 cm, (i) 0.108 cm, (ii) 0.308 cm, (iii) 0.908 cm
图3. 不同声带长度对应的声带表面压力分布图。(a) 0.01 cm and (b) 0.02 cm, (i) 0.108 cm, (ii) 0.308 cm, (iii) 0.908 cm; (c) 0.04 cm and (d) 0.08 cm, (i) 0.108 cm, (ii) 0.308 cm, (iii) 0.908 cm; (e) 0.16 cm, (i) 0.108 cm, (ii) 0.308 cm, (iii) 0.908 cm

Table 3. Vocal cord length of 0.908 cm
表3. 声带长度为0.908 cm
根据表1~3,可以得出对于相同的声带长度和声门直径,更大的声门下压在声门入口处造成更大的压降。如对于表1声带长度为0.108 cm的情况,当声门直径为0.01 cm时,500 Pa在声门入口处下降至−1141 Pa,1000 Pa下降至−2297 Pa,1500 Pa下降至−3457 Pa。此外,纵向对比不同声带长度,可以发现随着声带长度的增加,声门入口处的压力降减小,比如对于声门直径0.01 cm,声带长度0.308 cm,在声门下压500 Pa时对应下降至−462 Pa,长度0.908 cm对应下降至−60 Pa,提高了87%,在声门下压1000 Pa时,0.908 cm较0.308 cm提高了79%,在声门下压1500 Pa时提高了74%。对于声门直径为0.02 cm时,在声门下压500 Pa时,0.908 cm较0.308 cm提高了63%,1000 Pa时提高了62%,1500 Pa时提高了61%。其他直径和声门下压力条件下,可得到相同的结论。这一结果说明对于更长的声带长度,其用于驱动声带振动的空气动力更大。在声带振动周期开始时(向外张开),声带上受到的应力迫使声带进一步张开,直至张开到最大状态;在声带振动闭合过程中,增加的压力往往会缓冲碰撞并减小碰撞速度,从而能够从空气动力学上保护声带。因此,增加声带长度有利于声带振动,从而减小发声阈值压力。
5. 结论
本文主要研究了声带长度对声门管内压力场分布的影响。实验中首先构建声带的仿真模型,然后利用ANSYS前处理器Gambit进行网格划分,在确定初始条件和边界条件以及选择合适的湍流模型和计算算法后,用Fluent进行数值计算模拟出声带表面压力的变化情况。采用有限元方法进行计算机仿真,能够将肺部发声激励源对语音产生的影响考虑在内。实验结果表明:声带长度的变化对声带表面压力有重要影响。对于较长的声带,其声门管内压力分布在声门入口处较大,从而能够在声带振动周期中为声带张开提供较大的源动力以及在声带闭合中缓冲碰撞。同时进一步验证了Titze提出的发声阈值压力与声带长度的关系,增大声带长度有助于减小发声阈值压力,对改善声带损伤具有参考意义。实验中建立的声带模型为均匀声带模型,未考虑声带的倾斜角度,更进一步的研究应将声带的收敛和发散角度的影响因素加入实验中。
基金项目
国家自然科学基金(61271359)。