1. 问题描述
研究地下水渗透模型,保护有限的“生命之源”的任务越来越迫切,如何有效控制,并减少地下水污染等课题成为了当下不容忽视的问题 [1] 。在研究地下水污染物的在介质中的渗透扩散问题时,我们经常把此类问题转化为偏微分方程反问题来处理。
微分方程定解问题中的参数以及初始条件、边界条件等都是已知的,其相对应的偏微分方程反问题则是正问题的某个或者某几个已知条件变成未知,仅仅有和未知量有关的附加条件 [2] 等信息,我们所要做的就是根据方程本身、已知的几个定解条件和附加条件来求解问题中的未知量。
我们一般用一维Boussinesq方程来描述地下水运动情况,它是一个非线性方程,表示如下
(1)
式(1)中
为入渗强度;
是描述介质的透水性强度的一个参数,一般称之为渗透系数,在均匀介质中,渗透系数
在区域每个点上都是定值,在非均匀介质中,
是空间位置的函数,随着空间位置变化而变化 [3] 。根据偏微分方程的知识我们可以知道,如果
的值已知且满足光滑性条件,那么该问题的解是存在且唯一。这时的问题就是常见的正问题 [4] [5] 。
一般情况下,渗透系数的具体表达式是未知的,所谓系数反演问题,就是在只给定了
、
、
、
的表达式,而
是未知的情况下,来确定渗透系数
。在实际解决此类问题时,我们需要额外增加一些附加条件,通常会通过一些测量手段获得
在某时刻的近似值,再根据更多的信息或者测量数据来反演系数 k(x)。系数反演问题在工程实际问题中研究的比较多,在数学物理反问题研究中也有很重要的地位。
2. 一维Boussinesq方程反问题的不适定性实例构建
2.1. 实例一
考虑非线性一维Boussinesq方程初边值问题。作为参数辨识问题,在已知
,
的条件下,为了确定未知的渗透系数函数
及浓度的时空分布函数
,需要附加条件以确定解决问题的不适定性。文献 [4] 提出附加条件 ,从而认为对应的问题是适定的,并在数值算例中取未知函数的真值为
,
。将真值代入原方程我们可以得到相应反问题的已知条件实际设定为:
,从而认为对应的问题是适定的,并在数值算例中取未知函数的真值为
,
。将真值代入原方程我们可以得到相应反问题的已知条件实际设定为:
(2)
将式(2)中的已知条件代入式(1),我们得到自由项的表达式如下
其中
,并根据这些条件采用摄动量法求得
和
的数值解。
我们的疑问是:在增加附加条件
后,这一参数辨识问题是否是适定的?通过演算,我们得到的答案是否定的。即使完全已知
,由于关于未知函数
的一阶常微分方程为如下形式:
(3)
在不给定定解条件时,其解函数
也一定不会唯一的,因此问题求解的适定性也无从谈起。值得注意的是,在公开的文献中,这一问题并未受到关注,相应的反问题求解都是在增加同样的附加条件下进行的!有些文献中之所以得到比较好的结果,实际上是因为对
的函数类型做了限制,也就相当于提供了定界条件,相应地,算法的适应性就受到了较大的限制。
毫无疑问,上面给出的未知函数真值确实是反问题的解,但是即使已知
为给定形式,未知函数
仍是不确定的。事实上,将
代入Boussinesq方程,化简后比较方程两边关于t的多项式系数,得到
满足的三个等价的微分方程,其中二次项系数得到的方程最为简单,为如下形式:
(4)
解得
,其中C为任意实常数,显然,若想要唯一确定
,必须给定上述常微分方程的定解条件,通常情况下,定解条件可以设为
。
2.2. 实例二
在文献 [4] 中还给出了一个参数辨识实例,其初边值条件取值为:
(5)
未知渗透函数真值设定为
。
由于文献 [4] 未提供浓度时空分布函数
,这里根据初边值条件与
的相容性,猜测(不完全确定)
的真值设定为:
据此可推得
(6)
由式(3)和式(6)我们可推得
将上述表达式代入Boussinesq方程,化简后比较方程两边关于
的系数,得到
满足的微分方程为如下形式为
,从而可得
,其中C为任意实常数。
2.3. 实例三
除了考虑浓度时空分布函数
为稳态情形,即
与时间变量t无关,则Boussinesq方程可化为常微分方程
(7)
从而问题变为常微分方程下的参数辨识问题。
为验证偏微分方程反问题算法的有效性,可取
,
,则相应反问题的已知条件实际设定为
(8)
根据
满足的微分方程可解得
(9)
其中C为任意实常数。
2.4. 实例四
对于考虑
可分离变量的函数,记为
,将其代入Boussinesq方程,则有
(10)
在此基础上,我们构造实例四:在方程中,若取
,即浓度时空分布函数与空间位置无关,则必有
,从而我们可以知道,
也与空间位置无关,只与时间有关,所以这里将其记为
,则有
(11)
显然这里渗透系数函数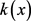 可取任意的函数,反问题的解存在但不唯一,具有严重的不确定性,所以再对其进行数值求解救没有任何意义。
可取任意的函数,反问题的解存在但不唯一,具有严重的不确定性,所以再对其进行数值求解救没有任何意义。
在方程中,为简单记,若取
即简单的线性函数,取
,则方程变为
,进一步地,假定
,则可得方程
。
此时若记
,则有
(12)
从而 ,
,据此不难设定数值计算实例,设定
,则
。
,
,据此不难设定数值计算实例,设定
,则
。
3. 总结
通过构建四个实例说明了一维Boussinesq方程反问题固有的不适定性,提出了求解反问题时附加条件的准确补充方式,构建的实例也为后续数值验证提供了依据。
NOTES
*通讯作者。