1. 引言
我们人类社会发展趋势的一个必然表现就是城镇化,城镇化是一个国家或地区现代化重要性的标志,也是工业化的重要性标志。我国城镇化正以惊人的速度快速推进,与此同时,我国的经济也以世界瞩目的姿态蓬勃发展。城镇化、经济增长是两个世界各国争相关注的话题,亦是学者研究的热门话题。Henderson [1] 曾尝试使用生产函数和不同国家不同时段的面板数据考察城市化与经济增长的关系,所得出的结论是,推动经济增长的并不是城市化本身,而是城市化的结构。沈坤荣、蒋锐 [2] 利用Cobb-Douglas生产函数,建立计量模型,并利用我国的相关数据进行了实证检验,结果表明:我国城镇化的不断发展能够通过影响物质资本、人力资本、知识资本和产业结构四种方式,进而促进和影响我国经济的不断增长。闫晓红 [3] 利用城镇化水平内生增长模型对我国27个省份20年的面板数据进行分析,表明除几个经济较发达的省区外,城镇化水平的提高对经济增长均有很大的推动作用。
因此,本文选取了这二者作为研究对象,试图挖掘出它们之间的关系。然而,本文最初在使用时间序列模型分析时,这二者之间的协整检验无法通过,即认为这二者不存在线性协整关系。因此促使我考虑使用非线性模型来对这两者进行建模、分析。
非参数模型相较于经典的线性模型来说更为灵活,不需要对模型施加过多的假设。光滑样条是一种非常流行的非参数回归方法,它不需要明确指定变量之间的函数关系类型,充分利用数据本身去选择合适的回归函数来拟合数据的变化趋势,能很好的解决变量之间的非线性建模问题。陈生长 [4] 比较了光滑样条回归、Monotonic回归、最小二乘回归三种方法,在一个记录了糖尿病人血糖和胰岛素测定值的数据集上进行拟合,从拟合误差角度,说明了光滑样条的拟合效果优于其他两种回归方法。本文选择光滑样条估计来研究我国城镇化率与经济增长之间的关系。
2. 自然三次样条模型
考虑在区间[a,b]上选择n个结点
,满足
,如果函数
满足:1) 在每个区间
,均是三次多项式;2) 在每一个结点上,
的一阶与二阶导数存在且连续。则这样的函数
被称为三次光滑样条。显然,三次样条函数可表示为:
(1)
如果三次样条函数
在a、b两点的二阶、三阶导数为0,则函数
被称做自然三次样条。
设有n对数据
,其中
,则可对数据
拟合模型:
(2)
假设
是满足以上条件的三次自然光滑样条,则令
,其中
,
,
,由自然边界条件可知q,
。令Q为
维矩阵,其元素
,
;
。
,
,则
;
;
,若
。又令R维
维对称矩阵,由元素
构成,
。
,
;
,
;
,若
。因此R是严格的正定矩阵,定义矩阵K:
。当且仅当
时,
。满足上述条件时g和
可以完全确定一个自然三次样条函数。
可以通过最小化函数:
(3)
来拟合得到样条模型。其中
是函数
的二阶导数,
被用来刻画函数的光滑程度;
是光滑参数,
的值越大,函数g越光滑。以下用向量来表示求解过程:
求
对g的偏导数,
令
,可得
。
的值可用
求得。在给定光滑参数
的值后,三次光滑样条可用以上向量形式表示。
如果
选的过大,对模型的光滑度的惩罚力度较大,会使得曲线过于光滑,导致过拟合;如果
选的太小,则对曲线的弯曲程度惩罚较小,会导致曲线出现过拟合。
可通过交叉验证法CV、广义交叉验证法GCV等方式选出一个最优的
。本文选用广义交叉验证(GCV)选择光滑参数
,
其中
。
3. 实证分析
本节在对我国城镇化水平与经济增长的关系进行研究时,选取了中国统计年鉴1978~2017共40年的数据。选取“城镇人口在总人口所占比重”这一指标分析我国城镇化水平,记为城镇化率X。因为人均国内生产总值将人口规模的影响剔除掉了,相对来说比较准确所以选取人均国内生产总值作为衡量经济增长的指标,记做Y。为了消除价格因素的影响,本节所采用的数据是以1978年为基期,经过计算得到的可比价人均国内生产总值。
3.1. 协整检验
对非平稳序列进行建模时,往往会出现“伪回归”现象,为了满足数据的平稳性,我们通常利用差分变换,使序列变平稳,但是这样建模的效果就受到了影响。我们通常可以通过协整来解决此问题,变量的协整检验最常用的方法是EG检验。
两变量检验的第二步,再对残差序列
的平稳性进行检验。由EVIEWS软件进行ADF检验,结果如表1。
通过检验结果发现,x与lny的线性组合所得到的残差序列
并不是平稳的,见表1,说明x与lny之间没有线性协整关系。造成此种现象的原因可能是,随着时间的推移,城镇化率对人均GDP的影响关系并不是线性的,而是每年都在变化的,因此,本文将使用光滑样条估计对数据进行分析。
3.2. 光滑样条估计
根据第二节中介绍的三次光滑样条的理论知识,利用R软件对模型进行估计。由于已有的大部分文献都是采用线性回归模型对其进行分析及预测,因此为了和线性回归模型进行比较,本文也对响应变量与预测变量进行了线性回归。图1是光滑样条与线性回归模型拟合的图像,较粗的直线是线性回归模型拟合的直线,较细的曲线是光滑样条拟合的图形,从图中可以看出光滑样条模型能够够好的拟合数据。

Figure 1. Fit of smooth Spline and linear regression
图1. 光滑样条与线性回归拟合
根据图2光滑样条估计的残差散点图可以发现,所有点都落在了−0.2~0.2的水平带状区间中,并且未表现出明显的趋势性,因此我们可以认为该模型具有良好的拟合效果。
因此,可以得出我国城镇化率与人均GDP的光滑样条模型:
在构建的线性回归模型中,将做过对数变换后的人均GDP作为响应变量城镇化率作为解释变量。利用R软件进行计算,并把结果汇总在表2中。
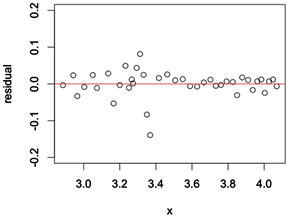
Figure 2. Residual plot of smooth spline
图2. 光滑样条估计的残差散点图

Table 2. Results of linear regression
表2. 线性回归的结果
我们可以得到预测方程:
为了分析模型的估计结果,本节把预测的均方误差作为评价标准:
通过表3可以看出,光滑样条估计的均方误差要比线性回归模型估计的均方误差小,说明光滑样条更好的拟合了数据。因此我们可以知道光滑样条模型的预测效果要优于线性模型。

Table 3. Root MSE predicted by two types of methods
表3. 两类方法预测的均方误差
4. 主要结论
从上一节的分析中,我们得到了光滑样条估计,并通过对比线性模型与光滑样条模型预测的均方误差得出光滑样条模型比线性模型好。同时,分析的结果告诉我们,城镇化率并不是以一种线性的方式影响着人均GDP的变化,而是以一种非线性的方式影响着经济增长的步伐。
光滑样条非参数回归分析不必假定反应变量与解释变量之间的函数形式,适用于任意分布的数据,因此光滑样条回归模型可广泛应用于经济学、医学等领域。
基金项目
北京市属高校基本科研业务费NO.110052971921/103资助项目。