1. 引言
随着现代工业和科学技术的发展以及自动化程度的进一步提高,机械正朝着大型化、高速化、连续化、集中化、自动化方向发展,生产系统中各设备之间联系也越来越紧密。由于各种随机因素的影响,这些设备不可避免地会出现一些故障现象,即降低或失去一定的功能;而设备一旦出现故障 [1] 就可能引起连锁反应,导致整个生产过程无法正常工作,造成巨大的经济损失,甚至还会引起严重的灾难性人员伤亡事故口。本文对故障信号识别进行研究,提取故障信号的各种特征,构建数据库与分类模型,对故障信号进行分类识别。对实验中振动行为信号样本采用监督模式识别方法进行分类:利用一定数量的样本作为训练集,首先进行特征提取,选择合适分类器模型,训练出一个分类超平面。对预测样本,经过相同特征提取算法,利用已经训练好的分类超平面判断行为类别,实现目标行为的智能、自动分析。
2. 振动信号目标特征提取及识别算法
对振动信号进行特征提取是实现故障诊断的前提条件,也是实现故障诊断的关键技术。实际工程中的机械结构往往较复杂,且零部件比较繁多,所以实际中采集到的动态信号是整个系统各个部件振动的共同结果,且在传输的过程中,也会受到传递途径的影响,这些使得采集到信号更加复杂,包含很多的无用信息。故在诊断过程中,需要对采集到的信号进行分析,提取相关的信号特征,然后分析其是否有相关的故障征兆,最后利用该征兆来进行故障诊断。
针对机械振动信号特征提取问题,国内学者提出了基于独立分量分析方法 [2] 、基于混沌振子的方法 [3] 、这些方法考虑单故障状态下局部零件的早期故障诊断问题。目前,最常用的信号特征提取方法是从时域角度直接分析信号波形进行特征提取 [4] ,该方法思路简单易于实现,但是由于信号采集现场环境往往比较复杂,诸如风、雨、动物等环境因素产生的波形与许多入侵行为波形极为相似,降低了系统对时域波形的判断。傅里叶分析 [5] 是信号处理的经典方法,对机械振动信号进行傅里叶变换,利用频谱或功率谱提取其频域特征,也是目前较为常见的方法,该方法在振动信号处理中效果较为理想。天津大学曲志刚等人提出使用小波 [6] 或小波包变换对光纤振动信号进行多层次分解,提取其在子频带的能量分布特征,该方法在石油、天然气管道安全检测系统信号处理中取得了较好的识别效果。
机器学习作为多元交织学科,综合了统计学、迫近论、算法时间复杂度等多门学科,常用的机器学习算法有K最近邻(K-Nearest Neighbor, KNN)、朴素贝叶斯、支持向量机(Support Vector Machine, SVM)等。湖南大学程军圣提取轴承信号时域特征和能量参数作为神经网络 [7] 的输入,有效识别故障类型。东南大学万遂人等则借鉴了语音信号识别的处理方法,将系统采集到的振动信号当成声音信号进行处理,利用隐马尔可夫模型(HMM)进行特征识别 [8] 。
2.1. Fourier分析
利用Fourier分析 [5] 实现振动信号时域和频域之间的相互转换,可以将原时域信号的研究转换为频域上的Fourier系数的研究。在信号处理领域,Fourier变换发挥了重要的作用,具有里程碑式的意义,它被看作是信号时域与频域之间的桥梁。对于信号x(t),其连续Fourier变换为:
(1)
其逆变换为:
(2)
在实际应用时,信号在时域和频域中往往是离散的,因此常用到的是离散Fourier变换(DFT),考虑到运算速度与系统消耗方面,快速Fourier变换(FFT)被广泛应用于信号的频域分析中。
2.2. 小波分析
小波分析 [6] 最早是由法国科学家Grossman和Morlet于80年代提出的,它与傅里叶分析相比,有突破性的进展,它具有时频域局部化的特点,能够使信号的细节部分特到显示,从而能够有效地提取特征信息。目前,小波分析在很多学科领域有着广泛的应用,如在故障诊断,图像处理、模式识别等。基于小波分析的故障诊断方法是基于信号处理故障诊断方法的一种,它不需要建立相应的数学模型,也不需要有先验知识,而且对输入信号的要求也比较低。同时,这种方法的计算量比较小,具有较强的克服噪声能力,而且灵敏度也很高,具有较大的应用空间。其基本理论如下:
小波函数ψ(t),它局部地存在于时域(空域)轴上,其波形可在特定的位置上发生变化:当对低频信号分析时,小波函数可以放大a倍;当对高频信号分析时,小波函数可以缩小a倍。小波函数ψa(t)是具有震荡特性、能迅速衰减到零的一类函数,可表示为:
(3)
其函数图像如图1所示:
设
是平方可积函数,ψ(t)是基小波或“母小波函数”,则
(4)
称为x(t)的连续小波变换(CWT),其内积形式为
。其中a (> 0)称为尺度因子,τ反映了小波函数在变换中的位移。常用的小波函数有Haar小波、Daubechies (dbN)小波系、Morlet小波、Mexican Hat小波、Meyer小波等。目前关于小波基函数的选择还没有统一标准,但是基于小波光滑性、正则性、对称性等特点本实验选取db3系列小波对原始时域信号进行k级多尺度分解。
2.3. 主成分分析
主成分分析 [9] (Principal component analysis: PCA)是一种统计方法。通过正交变换将一组可能存在相关性的变量转换为一组线性不相关的变量,转换后的这组变量叫主成分。其基本思路是寻找高维数据在低维空间重构误差最小意义下最优的投影子空间,从而用较少数目的特征向量刻画样本的全局信息,最终达到降低原始空间维数的目的。设样本矩阵为Xm × n (m个样本,n个特征),首先对样本矩阵X均值中心化,PCA希望找到一个方向w,使得样本投影到方向w上方差最大(主方向),优化目标为:
(5)
提取前k个主方向构成载荷矩阵
,则对原始样本特征提取后的结果为:
。
2.4. 支持向量机
支持向量机 [10] (Support Vector Machine, SVM)是一种常用的定性分析算法。它是Vapnik等人在统计学习理论和结构风险最小化(Structural Risk Minimization, SRM)原则的基础上,建立起来的一种通用的机器学习算法。它根据有限的样本信息,在模型的复杂性和学习能力之间寻求最佳折衷,以期获得最好的推广能力。其基本原理如下:
假设训练样本集
,其中
为第i个样本,
是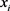 的标记,即第i个样本所对应的类别信息。在二分类问题中将其记做
。如果训练样本线性可分或近似线性可分,则一定可以找到一个最优超平面将两类样本正确分开,且使得两类样本到超平面的间隔最大。设该最优超平面为:
的标记,即第i个样本所对应的类别信息。在二分类问题中将其记做
。如果训练样本线性可分或近似线性可分,则一定可以找到一个最优超平面将两类样本正确分开,且使得两类样本到超平面的间隔最大。设该最优超平面为:
(6)
超平面将两类样本正确分开意味着:
(7)
其中
是引入的松弛变量,有:
即求解优化问题
(8)
求解最优分类面为:
(9)
3. 振动信号目标识别实验
3.1. 样本说明
实验测试数据包含六种状态:Healthy20Hz、Healthy40Hz、YangCo20HZ、Yangpa40HZ、YangUn20HZ、YangUn40HZ。每一类数据采集60秒左右,采样频率Fs = 10K Hz,包含四个通道(CH1、CH2、CH3、CH4),测得了10组数据。四个通道中六类典型样本的时域表示如图2~图5。从图中可以看出,四个通道中六类信号分布杂乱,从时域上很难将其区分开来。

Figure 2. CH1 six kinds of time domain samples
图2. CH1六类时域样本
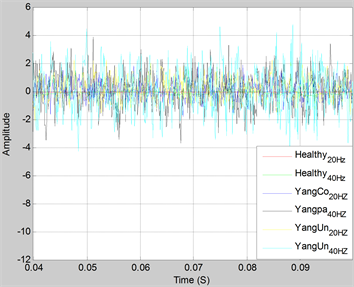
Figure 3. CH2 six kinds of time domain samples
图3. CH2六类时域样本

Figure 4. CH3 six kinds of time domain samples
图4. CH3六类时域样本

Figure 5. CH4 six kinds of time domain samples
图5. CH4六类时域样本
对数据进行连续小波变换(CWT)分析提取特征:基于小波光滑性、正则性、对称性等特点本实验选取db3系列小波对原始时域信号进行32级多尺度分解,以一通道信号(CH1)为例(图6~图11),从图上分析,同一通道中不同类别信号在小波域上具有一定差异性。
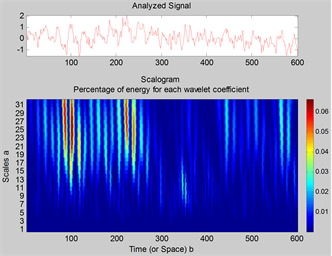
Figure 6. Healthy20Hz CWT chart
图6. Healthy20Hz CWT效果图

Figure 7. Healthy40Hz CWT chart
图7. Healthy40Hz CWT效果图

Figure 8. YangCo20HZ CWT chart
图8. YangCo20HZ CWT效果图
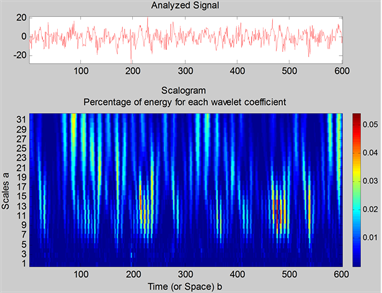
Figure 9. Yangpa40HZ CWT chart
图9. Yangpa40HZ CWT效果图
对每一段数据(60秒)进行分割,取1秒数据(一帧)为一个样本(每两个样本重合率为0.4)。实验样本信息见表1所示:
对六类光纤信号提取FFT特征(NFFT = 4096、Fs = 10K Hz),四个通道(CH1、CH2、CH3、CH4) FFT谱图均值如图12~图15所示:从该图中看出此六类样本在FFT空间具有一定的差异性。

Figure 12. FFT means of six kinds of CH1 samples
图12. CH1六类样本FFT均值
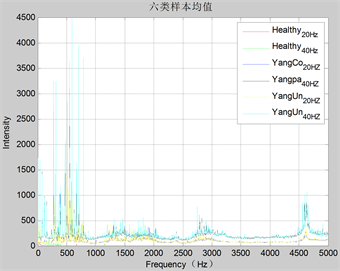
Figure 13. FFT means of six kinds of CH2 samples
图13. CH2六类样本FFT均值
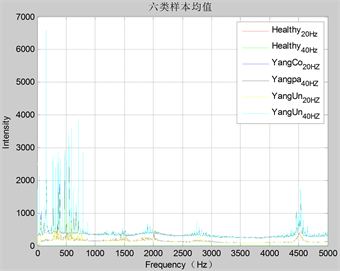
Figure 14. FFT means of six kinds of CH3 samples
图14. CH3六类样本FFT均值

Figure 15. FFT means of six kinds of CH4 samples
图15. CH4六类样本FFT均值
实验中特征提取及分类算法见表2所示:

Table 2. Feature extraction and classifier description
表2. 特征提取及分类器说明
3.2. 实验结果分析
为了分析样本在空间的分布状况,对FFT特征进一步提取PCA分析见图16~图19所示:从图中看出,通过PCA处理后六类样本在空间部分可分。

Figure 16. FFT feature of six kinds of CH1 samples for PCA chart
图16. CH1中六类样本FFT空间PCA效果图
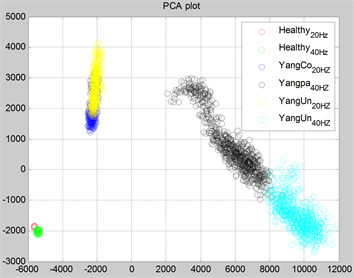
Figure 17. FFT feature of six kinds of CH2 samples for PCA chart
图17. CH2中六类样本FFT空间PCA效果图

Figure 18. FFT feature of six kinds of CH3 samples for PCA chart
图18. CH3中六类样本FFT空间PCA效果图

Figure 19. FFT feature of six kinds of CH4 samples for PCA chart
图19. CH4中六类样本FFT空间PCA效果图
为了准确评价FFT特征提取及SVM分类算法效果,对每类样本随机选取 [11] 0.75训练,0.25测试。该建模过程如图20所示:

Figure 20. Flow of supervised pattern recognition
图20. 监督模式识别过程
10次平均结果,测试总体分类正确率及每类样本分类正确率如表3所示:

Table 3. Comparison of classification results
表3. 分类结果比较
从上述四个通道(CH1~CH4)实验结果分析,仅利用CH1通道即可将6类振动信号基本区分开。
4. 总结
由于FFT样本在原始特征空间中具有一定的线性结构,所以基于PCA特征提取方法(线性变换)分类效果显著,同时利用SVM方法也取得了比较满意的分类效果。这是由于SVM基于结构风险最小化原则最大化分类间隔,特别针对小样本学习问题,具有良好的推广性能,随着后续训练样本的不断丰富,该方法也会进一步提高目标识别的正确率。