1. 引言
图像局部变形属于图像润饰的一种,通过插值映射的方式篡改图像,使图像局部产生像素移动的效果,常用于给图像中人物“减肥”,瘦脸等操作。Kee [1] 等人早在2011年提出认为过度润饰的图像会严重影响到青少年心理的健康发展,以及对社会信任的产生不好的影响。他们提出了一个度量来量化标记数字图像篡改的程度,但是这种度量是在存在原始图像的前提下的,通过原始图像与篡改图像的对比来计算篡改图像的篡改程度。其篡改程度包括了主题面部和身体上的几何变化的修正程度,但是并不能检测图像是否发生局部几何变形篡改。
Bharati [2] 等人提出了一种新的使用有监督的深度玻尔兹曼机的算法,在人脸图片中选取了4个部分学习特征,通过使用提出的算法判别人脸图像是修饰过的还是原始图像。该方法并没有检测图像是否发生变形篡改以及定位篡改发生的位置。
Hwang [3] 提出了一种图像局部变形的检测方法,他们通过研究几何变换中的差值模式,提出了一种重新插值的方法检测几何变形,但是这种需要直观观察的方法在图像局部几何变形中的检测效果并不是很理想。对于压缩图像的篡改的检测效果更是不好。图1显示了使用Hwang的方法检测图像局部集合变相的结果。
图1(a)代表的是原始未篡改的图像,图1(b)和图1(c)显示的是未压缩图像的局部变形图形及其地面真是图像,图1(d)表示使用Hwang的方法检测篡改图像1,即检测未压缩图像的检测结果。图1(e)是对原始图像压缩后进行篡改的局部变形图像,图1(f)是篡改图像2的地面真实图像,图1(g)是使用Hwang的方法检测压缩图像的篡改图像的结果。Hwang的方法在图像纹理比较均匀位置的检测效果较好,如图1(d),图1(g)右上部分篡改处的检测效果,能够很明显的显示出篡改位置;而在图像中物体边缘处的检测结果不好,图中对气球边缘位置篡改的检测在检测结果图1(d),图1(g)中并不容易观测到。另外对于压缩图像的检测结果2观察发现其呈现8 × 8的分块现象,图1(h)是对于图1(g)局部放大的显示结果,能够明显观察到小块的存在,而在篡改区域的小块是不完整的,这种现象和块效应现象不谋而合。我们认为其能够为块效应的检测提供一定的帮助。

Figure 1. Detecting local deformation of image after scaling of 1 pixel
图1. 1像素缩放后检测图像局部变形
目前大众接触到的图像更多的是压缩过的图像,JPEG压缩方式是最常见的一种压缩方式,很多图像取证技术要求图像是未压缩的高质量原始图像,并且其对压缩图像的检测效果会大打折扣。而基于图像压缩的方法可以用来识别压缩图像的篡改操作,常见的基于压缩图像的检测方法主要包括:基于JPEG量化 [4] 、基于双重JPEG压缩 [5] [6] 、基于多JPEG压缩 [7] 和基于JPEG块效应 [8] 。
JPEG在压缩的过程中是对图像进行分块处理的,对每个压缩块计算其离散余弦变换(DCT),这种压缩方法使得图像不同块之间的关系发生弱化,块中像素相关性较大而块间的像素相关性变弱,造成快件出现断层,即块效应。块效应常用来检测图像的复制粘贴及拼接操作,人们在对图像进行上述篡改操作时主要考虑将复制或剪切的部分放置在图像的合适位置,并不考虑图像的块效应是否一致。同样,在对图像进行局部变形时会改变变形区域像素的值,使像素发生移动的现象,这种情况破坏了压缩图像的块效应。图2展示了对于压缩未篡改图像的块效应网格以及压缩篡改图像的块效应网格。

Figure 2. Block effect grid for compressed images
图2. 压缩图像的块效应网格
图2中展示了压缩图像的块效应网格。其中图2(a)显示了对压缩但是没有发生局部变形的图像,图2(b)显示了对压缩图像进行局部变形后的篡改图像,图2(c)显示的是地面真实图像,图2(d)和图2(e)都是使用Li [9] 的方法分别对图2(a)和图2(b)提取块效应网格的结果。没有发生图像局部扭曲的位置呈现较好的块效应网格,在图像发生局部变形的位置的块效应网格也变得混乱,不在呈现出网格的效果。
我们依据Hwang的图像局部变形检测方法以及Li的块效应方法,提出了一种改善块效应检测局部变形的方法。我们首先使用Hwang的方法提取图像缩放图像的残差结果图像,对残差结果图像以8为周期题块效应网格,并使用新的特征来检测图像变形篡改发生的位置。
2. 提出的方法
我们根据上述发现提出了一种检测局部变形的方法,且该方法的检测效果改善了直接使用块效应的检测方法。我们方法的流程图如图3所示。
对于输入的图像我们的第一步使用了Hwang的方法提取差值图像。对于得到的差值图像,提取其块效应网格,并提取网格特征,通过分析网格特征得到最后的检测结果图。在提取块效应网格时,我们主要借鉴了Li的方法,但是在其方法及特征选择上有所改变。
2.1. 缩放残差图像提取
我们方法的第一步是提取待检测图像的1像素缩放的残差图像,其中使用了Hwang的方法。对于篡改图像使用重新插值的方法对其进行处理,对大小为
的图像使用最小重新插值的方法,先进行
像素缩小,后进行
像素的放大。之后输出重新插值图像和待检测图像之差的残差图像,其算法如公式(1)所示。
(1)
(2)
(3)
对于图像缩放的每一步都使用双三次差值方法,其卷积核使用公式(4)。
(4)
其中a的值为0.5,给定点
进行插值,我们使用的二维三次卷积函数如公式(5)。
(5)
其中
是三次卷和,即公式(5-4),Cij是插值系数。
之后使用公式(6)对提取图像的1像素缩放后的结果,用D
表示。
(6)
2.2. BAG提取
由于使用图像缩放的方法得到的差值图像已经基本显示出来了要图像的块效应网格,我们不再对图像使用绝对二阶差分。BAG线的特征是由水平线和垂直线构成的,并且在这两个方向上有固定8的周期,所以我们分别提取水平和垂直方向的块效应网格。
2.2.1. 提取弱水平线Eh
在提取弱水平线
时,我们对的得到的1像素缩放的差值图像使用公式(7),通过对每33列水平累加以放大D中的弱水平线,
是
中的一个元素。
(7)
之后使用公式(5~8)获得弱水平边缘
,
(8)
其中函数
返回集合
中的中值,
为图像
的元素。
2.2.2. 从图像Eh中提取具有8周期的行
为了减少噪声的影响,使用公式(9)对弱水平图像
进行周期性中值滤波。
(9)
其中
是提取的水平BAG线图像
中的元素。
类似的,可以提取垂直方向的BAG线图像
,之后使用公式(10)将
和
结合,得到最终的BAG图像。
(10)
其中
是提取的垂直方向的BAG线图像
中的元素,
是提取的最终的BAG图G中的元素。图4展示了对于图2中的篡改图像分别使用Li的方法及上述方法提取块效应网格的结果。
图4(a)是直接对压缩后的篡改图像提取的块效应网格,图4(b)显示的是对于缩放后的差值图像按照上述方法提取的块效应网格。在篡改区域的块效应网格明显是不成块的,在未篡改区域有块效应较明显,另外整体来看对1像素缩放的残差图像提取的块效应网格在图像边缘处的处理更好。
2.2.3. 计算图像G的特征f
对于一幅未篡改的图像的块效应网格应该是一致的,其表现图像性类似于图5(a),而图像局部变形处的块效应则会变得没有规律,显示如图5(b)所示。
 (a) Untampered block
(a) Untampered block  (b) Tamper block
(b) Tamper block
Figure 5. 8 × 8 Block effect grid of image
图5. 图像8 × 8块效应网格
从图5中可以看出块效应的规律,对于一个完整的8 × 8小块,其周围一圈的值是大于内部的值,而篡改处的8×8的小块则不具备此规律。Li提出的特征是用来检测图像赋值粘贴和移动篡改的,其在篡改区域可能也出现块效应,但是两部分的块效应是不匹配的,依据块效应的不匹配来检测篡改。而图像的局部变形是完全打乱了图像的块效应,所以可以直接判断是否存在块效应来检测篡改的位置。我们使用8 × 8小块每部位置值的平均值减去周围值的平均值来判断图像块是否符合块效应的规律来判断图像篡改,如公式(11)。
(11)
其中ave[]返回的是平均值,b是特征偏移量。对于篡改位置,由于像素的移动,使得块效应变得不规律,其可能出现外圈与内圈相差不大的情况。通过观察提取的f特征结果,在篡改位置附近,特征f的取值是接近0的,所以需要进行f特征偏移来确定最终的使用的特征,通过实验我们发现将特征f进行加3的偏移会得到较好的检测结果,该参数值3是一个大致值,其选择我们在实验部分介绍。
3. 实验分析
本次实验使用的数据库 [10] 中的图像,对于下载的原始图像,我们使用Photoshop工具对其进行处理。首先是以质量因子5对图像进行压缩处理,之后对压缩的图像使用Photoshop中液化工具进行局部变形处理。对篡改保存后的图像进行实验研究,我们使用matlab2016实现算法。
3.1. 特征偏移参数选择
本节我们研究特征偏移参数的选择,我们使用图2中的篡改图像进行实验,不同的偏移量的检测结果展示如图6。
图6(a)展示的是对篡改图像直接使用Li 方法检测块效应的结果,图6(b)~(f)使用的是我们的方法的检测结果,但是特征偏移量的选择不同,偏移量分别是−1、0、1、3、5。通过观察发现偏移向负值使得检测结果变差,当偏移量向正值后效果会好,但是超5之后误检的情况会变多。使用偏移量后随着偏移值的加大在图像四个角的位置会出现更多的误检,综合图像中部的检测效果来说,我们选择3作为我们的偏移量。
3.2. 方法实验结果
实验的部分结果展示在图7中。
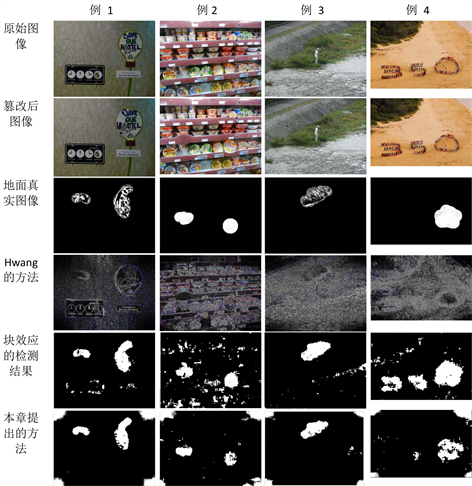
Figure 7. Some experimental results are shown
图7. 部分实验结果展示图
图7展示了我们的部分实验结果,第一行展示的是原始未篡改的图像,第二行展示的是局部发生篡改的图像,第三行展示了是篡改图像中发生篡改的位置,白色部分是篡改的位置。第四行展示了使用Hwang方法检测压缩图像的篡改结果,对于压缩图像使用Hwang的方法检测篡改,在图像中物体边缘人眼很难分辨出是否发生了篡改。第五行展示的是对于篡改图像直接使用块效应来检测局部变形位置的结果,第六行展示的是本节提出的方法的检测结果。我们的方法的检测结果在四个角出会出现误检,这是由于对图像进行缩放时造成的。但是由于人们使用的图像变形操作更多的是在图像中心主题位置进行的,所以我们更应关注中心在主体位置的检测效果。从实验中可以明显看出,使用我们的方法在图像的主体位置有更好的检测效果。
4. 总结
本文我们对压缩图形的局部变形进行研究,图像的局部变形使变形区域的像素值发生变化,破坏了压缩图像的块效应,因此可以使用块效应来检测压缩图像的局部变形。另外通过研究Hwang的方法,我们发现其方法能够对压缩图像产生块的现象。基于上述两点,我们提出了对待检测图像使用1像素缩放后的残差图像提取块效应,并使用新特征检测图像局部变形的方法,对比直接对图像使用块效应的检测方法有了较好的检测结果。
参考文献