1. 引言
系统性风险一直是监管层、学术界关注的重点,早在1991年就有学者提出金融体系爆发系统性风险的可能性高于其他任何体系。2008年金融危机以后,学术界对于系统性风险的概念认知更为清晰,国际货币基金组织、国际清算银行均认为系统性风险是金融系统部分或者全部受到破坏而导致金融系统大范围的功能失效并给实体经济带来重大灾难的风险。据学者研究分析,系统性风险具有溢出传染性(范小云,2002 [1] )、危害范围广(张晓朴,2010 [2] )等特点。鉴于本文的研究角度,我们提出,系统性风险就是在初始冲击下,一个或多个机构受损,导致系统中其他个体相继受损至不可控时,进而威胁到整个体系甚至社会经济发展的一种多米诺骨牌式现象。
当今世界,全球化的不断演变与发展、各类经济体之间的联系越发密切,一方面可以充分利用资源实现最优配置、促进经济发展,但另一方面,会造成风险更容易入侵,为监管层测度与防范风险带来了更多的难题。目前,中国金融体系正面临的如下挑战:一是金融同业业务发展迅速,由此导致银行间网络风险逐步积累,2013年的钱荒正是银行间市场流动性风险的标志性事件;二是随着经济发展、金融自由化程度不断提高,银企间借贷交易急剧增长,据银监会的数据显示,2018年三季度末商业不良贷款率1.87%,较上季末上升0.01个百分点;三是中小企业在经济中的地位不断攀升,中小企业为了避免资金链断裂,会通过互保、连环担保等担保方式向银行贷款,这种企业辅助融资机制一度促进经济发展,然而,受信贷市场膨胀和经济下行的影响,担保风险不断浮现,对实体经济和银行业均造成了重大创伤。2017年10月,党的十九大报告要求,“健全金融监管体系,守住不发生系统性金融风险的底线”。习近平总书记反复强调,“金融安全是国家安全的重要组成部分,准确判断风险隐患是保障金融安全的前提”。
我们对系统性风险的测度方法进行了大量的探索,将测度方法大致分为以下三类:一是综合各类指标制定宏观指数测度整体状况(Kaminsky等,1998 [3] ;Illing等,2006 [4] ;Renne,2014 [5] )。然而由于财务数据的滞后性,用综合指标测度金融系统性风险的时效性不足;且关联性的不可忽视促使越来越多的人认识到网络的重要性以及应该在系统层面研究风险问题。二是测度系统重要性金融机构,如CoVaR (Adrian等,2014 [6] )、SES (Acharya等,2017 [7] )均可以量化单个金融机构对金融系统性风险的边际贡献,然而无法描述金融机构之间风险的动态传染途径。三是基于复杂网络模型研究市场关联所导致的金融体系脆弱性,这可以追溯到2000年,Allen等 [8] 研究了银行间网络结构对系统性风险的影响得出风险传染主要取决于银行之间的连接方式,完全连接网络(每家银行都和其他的银行有对称的资产负债关系)比不完全连接网络(每家银行只与一部分银行有资产负债关系)要稳定。而后大量学者表明金融系统性风险与金融网络的拓扑结构有关(Nier等,2007 [9] ;Haldane等,2011 [10] ;Roukny等,2013 [11] )。
在网络模型的基础上,可以将不同因素对风险传染的影响可视化,基于网络模型的方法主要将金融复杂系统抽象为网络结构,并研究其中的风险传染。拆借关系和借贷关系可以统一看作贷款关系,只不过二者主体不同,前者是银企间,后者是银行间。现有研究主要集中在银行间网络(Upper等,2004 [12] ;Boss等,2004 [13] ,2005 [14] ;范小云等,2012 [15] ;王明亮等,2013 [16] ;欧阳红兵等,2015 [17] ;Iori等,2015 [18] ;李政等,2016 [19] ;Lux,2015 [20] ):Upper等(2004) [12] 从银行资产负债表数据中估算双边信贷关系矩阵,利用德国银行间市场数据实证得出不完整结构比完整结构更容易扩散风险,如果银行间贷款的损失率超过约40%,一定会发生大规模的蔓延。Boss等(2004) [13] 通过研究奥地利银行间市场数据集得出银行间网络是一个小世界,系统中任何两个节点之间的分离程度非常低。Boss等(2005) [14] 表明奥地利银行的平均违约概率低于1%,只有小部分银行违约才具有传染性。王明亮等(2013) [16] 根据银行业数据构建银行间网络,利用矩阵法模拟分析了不同网络结构和不同风险冲击下单个银行倒闭引发的传染危机效应。欧阳红兵等(2015) [17] 通过对银行间同业拆借市场进行的实证分析证明了最小生成树和平面极大过滤图方法构建和分析金融市场网络对系统性风险测度的有效性和稳健性。李政等(2016) [19] 通过网络分析法解构了金融网络的总体关联性以及部门内和部门间的关联特征,并采用金融机构微观层面的数据实证分析了网络关联的影响因素。范小云等(2012) [15] 构建网络模型并利用银行年报数据分析得出负债关联程度对系统性危机有着重要影响。Lux (2015) [20] 基于给定银行规模的资产负债表结构,构建了基于银行信用关系的内生动态网络模型,得出优惠利率的实施有利于降低周边小银行系统性风险。
相对银行间网络的研究,对银企间借贷网络的研究较少:Fujiwara等(2009) [21] 提出了一种新的方法来解释商业银行和企业之间的信用关系,并用这种方法检查1980年至2005年日本信用网络结构的变化。Masi等(2011) [22] 利用网络理论的工具,对2004年日本的银行与企业的信贷市场进行了分析。Gatti等(2009 [23] , 2010 [24] )通过下游和上游企业间的借贷关系以及企业和银行的借贷关系研究了三部门网络经济的特征,发现一个企业的破产可能会导致一个或多个其他企业或银行破产,这取决于网络结构和所涉及的资产负债表上不良贷款率。Asanuma (2013) [25] 探讨了多家企业和一家银行组成的经济网络,模拟结果表明,银行的贷款态度通过信用网络显着影响经济系统的动态。Thurner等(2013) [26] 构建了由企业和银行组成的经济网络,论证表明可以通过提高透明度或者一些强制规则减少同业拆借来降低系统性风险。
担保关系也可以抽象为一种复杂网络,其关联性极易造成风险的连锁反应。2013年温州担保圈的危机不仅使得众多企业深陷其中,也使得银行业遭受巨大损失,可以说是对实体经济和虚拟经济均造成了重创。在担保合约中,借款方的违约会导致担保方承担还款责任,而担保方的质量下降也会提高借款方的融资成本(Cook等,1996 [27] )。Kiyotaki等(1996) [28] 发现当部分企业遭受负面冲击后,风险可能通过上下游企业商业信用形成的信用网络发生连锁反应。Upper等(2004) [12] 指出互保或联保的压力效果和抵押贷款一样,甚至更强。在商业集团中,单个企业所面临的负面冲击可能殃及整个集团公司,产生传染效应(Banal-Estañol等,2013 [29] )。罗刚等(2015) [30] 利用企业间的担保关系数据构建网络得出风险的传播与网络的拓扑结构密切相关,入度较大的节点发生风险容易在短时间内使风险在网络中迅速蔓延。徐攀等(2018) [31] 选择SIRS模型构建风险传染模型分析中小企业集群互助担保网络风险传染,结论表明:传染效应并不总是发生,只有当有效传染率大于风险阈值时,传染效应才会沿着互助担保链条蔓延扩散。
随着网络科学理论的发展,从系统层面研究金融风险的方法有所突破,从基于单层网络的视角逐步发展到基于多层网络的视角研究风险传导。目前,已有学者基于多层网络视角研究金融网络的拓扑结构(León等,2014 [32] ;Bargigli等,2015 [33] ),而基于多层网络的视角研究金融风险传导主要集中于单主体多关联的形式(Montagna等,2013 [34] ;S Poledna等,2015 [35] ;Sebastian等,2015 [36] ;Peralta等,2016 [37] ;Korniyenko等,2018 [38] ):Montagna等(2013) [34] 基于长期贷款、短期贷款和持有共同资产三层考察个体传染者对系统性风险的溢出贡献得出多层网络上测量的系统性风险远大于来自各网络层的聚合风险,且系统性风险与金融多层网络拓扑结构有关。S Poledna等(2015) [35] 也指出仅在单层网络中测度,风险会被大大低估,并量化了2007年至2013年墨西哥银行的四层关联对系统性风险的贡献。Sebastian等(2015) [36] 根据银行间衍生品、证券交叉持股、外汇、存款与贷款四类市场组建了多层网络,并分析其系统性风险。Peralta等(2016) [37] 基于有无抵押交易类型将银行网络结构划分为两层,研究结果表明多层网络结构下的金融风险传染更为迅速,而交易多元化可有效降低银行系统性风险。
2. 基于银企间多层金融网络的模型构建
2.1. 银企间网络模型的构成要素
本文建立一个以银行和企业两类主体为节点的多层网络,包含
个节点,分别是N家银行和M家企业。如图1所示,第1层是银行间的同业拆借关系层(实线指代拆借关系),理论上存在与其他节点无任何关系的节点,故假设至多存在N个持有风险资产的银行b,第2层是银行与企业的借贷关系层(点线指代借贷关系),同理,至多存在N个持有风险资产的银行b和M个企业f,第3层是企业向银行借款而存在的担保关系层(虚线指代担保关系),同理,至多存在M个持有风险资产的企业f。定义构建的复杂多层金融网络模型为
,集合V中的各节点表示银行b、企业f;当借贷关系或者担保关系存在时,银行之间、银行与企业之间或者企业之间存在联系,记作l,属于集合E。
金融风险是在金融市场运营中的不同参与者之间相互作用中产生的,本文建立银企间多层网络模型来描述不同参与者之间的关联性,关键在于确定不同参与者之间的债务债权关系。我们用邻接矩阵
来表示各节点之间的关系,
表示不同层:银行间同业拆借层(第1层)、银企间借贷层
(第2层)、企业担保层(第3层);
表示第
层上的第i个节点拥有第j个节点的债权金额,相当于i的风险敞口,按惯例方向是从节点j指向节点i;统一定义
表示不存在自己对自己的债权。
对于银行间的同业拆借层(第1层),银行j向银行b借款,因为存在无法还款的可能性,则该笔借款
对银行b来说是一项风险资产;再者银行间的同业拆借往往期限较短,目的在于平复银行间流动性盈亏,解决临时性的资金短缺,因而银行间同业拆借结构与银行间同业拆借行为同步演化,是一个动态网络层。同理,企业f向银行b借款,因为存在无法还款的可能性,则该笔借款
对银行b来说也是一项风险资产;且无论长期借款还是短期借款,均是一个不断演化的过程,因而银企间借贷层(第2层)也是一个动态网络层。另外,如果企业f向银行b借款过程中存在第三方担保企业1k,即存在担保关系,网络中出现企业间担保层(第3层)。担保方所承担的债务属于从属借贷合同的债务,也是一个动态演变的过程,所以企业间担保结构也是一个动态网络层。

Figure 1. Simplified network structure
图1. 简化的网络结构图
2.2. 银行和企业两类主体的微观结构
在微观层面上,该多层网络中的所有节点都满足资产负债表的特征,且不同节点的资产负债表之间存在一定的联系。因此本文将使用简化的资产负债表代表每个节点的状态,以期能够量化整个网络的动态变化。
银行的资产
细分为银行间资产
、银企间资产
、其他资产
;银行的负债和权益栏分为银行间负债
、其他负债
和权益
,如表1所示。对于银行b的资产负债表中每个同业资产
,在银行j的资产负债表中都存在与之对应的负债,即
,故银行间负债
;并设定其他负债
;权益
作为损失缓冲器,
;且
关系恒定。
同理,简化的企业资产负债表如表2所示,将企业的资产
细分为流动性资产
和非流动性资产(其他资产)
;企业的负债和权益栏分为银企间负债
、其他负
债
和权益
;显然两张资产负债表中,企业的银企间负债与银行的银企间资产是相互对应的;权益
作为资产缓冲器,
;且
关系恒定;另外,由于担保业务属于表外业务,而企业对外提供担保实际上形成了或有负债,因而一旦企业被要求履行担保义务时,体现在资产负债表上为资产受损,这里假定流动性资产受损。

Table 1. Simplified bank balance sheet
表1. 简化的银行资产负债表

Table 2. Simplified firm balance sheet
表2. 简化的企业资产负债表
3. 基于银企间多层金融网络的风险传导机制
3.1. 简化的风险传导机制
银行间的同业拆借、银企间的借贷关系均可以对资金进行有效的配置,且溶出资金方也就是债权方可以从中获得利益。然而,同业拆借和借贷在为债务银行或借款提供了便利的同时也为风险传导提供了渠道,形成了一张利益交错、风险共担的网络,一旦风险爆发将触发金融脆弱性。而在现实中,银行和企业间的信息不对称会导致一系列的问题,为了降低银行监督成本、企业融资成本,银行会提出担保的要求,因此,在银企间的借贷关系中通常还存在一些企业间的担保关系。担保往往依托于社会关系,形成于彼此较为熟悉的人群内部,可能是血缘、亲缘、地缘、业缘等关系。那么企业通过担保方式向银行贷款,这种企业间的担保关系其实是深深嵌入于某种社会网络或者社会纽带之中的,从而使得风险网络更为复杂。
无论是企业还是银行,产生风险的原因有很多,本文主要归为两大类:主动传染和被动传染。主动传染主要是由于自身经营等方面出现问题导致其难以为继,从而破产清算;而被动传染是指在市场经济中,由于自身与其他企业或银行产生经济关联而可能造成资产损失,一旦损失过多将导致其无法正常运行从而被迫破产清算。同时,任何一个企业在不同的合同中扮演不同的角色,比如在与银行的借款合同中是借款方,也可以是从属于其他企业与银行借款合同的担保合同中的担保方。同理,银行既可以是债权方,又可以是债务方。如图2所示,将市场经济体制中的银行间、银企间以及企业间的相互关联抽象出来,形成一个完整的风险传导机制。即在外部冲击下,被冲击的企业或银行的权益受损。因为系统中

Figure 2. Simplified risk conduction mechanism diagram
图2. 简化的风险传导机制图
的银企间存在借贷关联、银行间存在拆借关系、企业间存在担保关系,预计被冲击的银行将会把权益损失线性地传给债权银行;而被冲击的企业将会把权益损失线性地传给担保企业再进一步传导至债权银行、或直接传给债权银行。债权银行采取抽贷等措施进而导致风险回到被冲击企业,这一系列风险传染过程将引发系统性风险爆发。
在风险传导过程中,大致分为以下三种风险传导方式:一是风险单向传导方式,即网络结构中的一个节点x1受冲击,则风险会传向与之相关的节点x2,紧接着节点x2将风险传向与相关的节点x3,节点x3传向节点x4……这种风险传导方式会对风险进行分散和稀释;二是风险加迭代传导方式,即网络结构中的一个节点x1受冲击,则风险会传向与之相关的节点x2,紧接着节点x2将风险传向与相关的节点x3,节点x3传向节点x1……这是因为网络结构中存在闭合回路,风险将逐步累积直到爆发;三是风险加速传导方式,即网络结构中的一个节点x1受冲击,而债权银行x2可能会实施抽贷行为,这将加速风险的爆发。显然这三种方式共存于现实中的风险扩散中。为了重点论述多层网络中的系统性风险传导机制,本文进行分类探究和分步探究。分类探究可以描述各层内部节点受到冲击后的一系列连锁反应来模拟风险传导机制,见3.2、3.3和3.4;分步探究将说明风险是如何一步一步扩散至整个网络的全过程,见3.5。
3.2. 银行同业拆借层的风险传导机制
在该层任选三个节点:银行j,银行b,银行i。银行j向银行b借入资金,银行b向银行i借入资金。初始状态,银行j从银行b借入资金,如果银行j受到冲击,设置冲击比例
,反映外部冲击力度的强弱以及对被冲击银行或企业造成的损失程度。受到冲击的银行
的其他资产减少
。银行受到初始冲击可能破产违约,即使并未违约信用恐慌仍会随着信贷关系传播使得债权银行的银行间资产减少、权益受损。
即存在两种可能,一是银行j可能无法抵制冲击破产,那么银行b的银行间资产中与银行j相关的部分预计减少至0;二是银行j能够抵制冲击,假定负债不变,那么资产的变动直接反映到权益,即权益损失
。损失将随着同业拆借关系由银行j传染至银行b,那么银行b的银行间资产中与银行j相关
的部分预计减少至
。银行b会将该信用风险进一步传染至银行i。

Figure 3. Risk contagion mechanism of the interbank lending layer
图3. 银行同业拆借层的风险传导机制
如图3所示,债务银行受到冲击,导致风险在银行同业拆借层中通过资产负债表渠道扩散,一旦涉及到信用风险的银行达到一定的数量,将会在银行间形成链式传染。而在银行同业拆借层中,风险敞口是银行间的同业拆借款,这对债权银行来说均为流动性较强的资产,该类资产受损时,对银行的资产流动性影响较大。因而一旦同业拆借银行间形成链式传染,极易引起流动性风险。市场中出现的流动性困境带来的影响体现在很多方面,如债权银行因其自身的债务不变,面临着到期还款困难的窘境,不得不出售资产。而市场流动性恶化,银行出售资产时很难在不发生损失的情况下变现,即其资产以一定的折扣率交易,银行需卖出大于账面的资产来弥补资金短缺,这也将导致银行的权益损失。
3.3. 银企间借贷层的风险传导机制
在该层任选三个节点:企业f,银行b,银行i。企业f向银行b借入资金,银行b向银行i借入资金。首先是外部冲击的影响,外部风险冲击企业f,则被冲击企业的权益受损,即
。借款企业受到初始冲击可能破产违约,即使并未违约信用恐慌仍会随着信贷关系传播使得债权银行的银企间资产减少、权益受损。同时,对于银企间借贷,在还未到协议规定的还款期限期间,银行认为企业经营出现问题,可以提前要求企业还贷来收回贷款。
因而存在三种可能,一是企业f可能无法抵制冲击破产,那么银行b的银行间资产中与企业f相关的部分预计减少至0;二是在企业f可能无法抵制冲击破产前,银行b已经认定企业f经营不善,将实施抽贷行为尽可能保护自身资产不受损,假设抽贷行为将避免银行间资产的损失,因而银行b的银企间资产中与企业f相关的部分预计没有改变;三是企业f能够抵制冲击,但损失将随着借贷关系由企业f传染至
银行b,那么银行b的银企间资产中与企业f相关的部分预计减少至
。接下来,银行b会将沿着同业拆借关系将该风险传染至银行i。
如图4所示,在银企间借贷层中的风险传导与银行同业拆借层的风险传导相似,风险通过资产负债表渠道传染,在银行间形成链式传染,引发流动性风险,进而产生系统性危机。
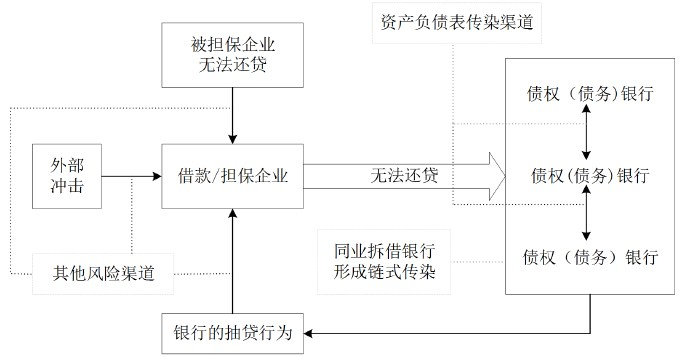
Figure 4. Risk contagion mechanism of the lending layer between banks and firms
图4. 银企间借贷层的风险传导机制
3.4. 企业担保层的风险传导机制
在担保方式中,有两个较为常见的方式,一是互保,即企业f为企业k作保、企业k为企业f作保;另一个是连环互保,即企业k为企业f向银行借款作担保、企业r为企业k向银行借款作担保、企业f为企业r作担保。总体而言担保方式复杂、担保关系隐蔽在借贷关系中,企业间一旦形成担保链式传染将造成严重后果,因而涉及担保的企业应当被纳入监管范围。

Figure 5. Risk contagion mechanism of the firm guarantee layer
图5. 企业担保层的风险传导机制
在该层任选三个节点,企业f,企业k,企业r。企业k为企业f向银行借款作担保,企业r为企业k向银行借款作担保。一旦企业f受到外部冲击无法还款,那么企业k将为企业f承担债务,那么风险将从企业f传导至企业k;而企业r为企业k担保,因而企业k出现财务困境会牵连企业r,即风险再传导至企业r。
外部风险冲击企业f,则被冲击企业的权益受损,即
。借款企业受到初始冲击可能破产无法还贷,那么企业k作为担保方有义务承担该笔负债,担保企业k的资产受损。当然担保人所承担的债务属于从属债务,所以这笔负债
。
同时,对于银企间借贷,在还未到协议规定的还款期限期间,银行认为企业经营出现问题,可以提前要求企业还贷来收回贷款。一旦k企业被迫提前还贷却无力支付时,担保企业r因担保责任需要承担该笔借款。这种因借款方无法履行到期债务而担保方受牵连的风险也是信用风险中的一种。且该风险将随着企业担保关系不断扩散,形成链式传染。
担保链本质上是一种企业信用增进机制,能够在短期内有效化解链上企业融资困境,但这种融资模式也会产生并传播企业危机。如图5所示,一旦一家企业出现问题,风险将沿着担保关系不断传导,最终导致担保企业形成链式传染,造成区域性的企业经营困境和局部金融风险。
3.5. 分步骤的风险传导机制
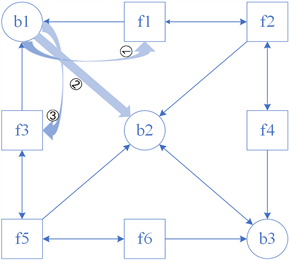
在风险传导机制的细化步骤图中,字母b代表银行,字母f代表企业,蓝色细直线代表银行与企业间的借贷关系、银行间的拆借关系以及企业间的担保关系,如图6(1)所示是一个简单的关系网络结构图。
图6(2):银行b1受到外部冲击,其权益受损,因为企业f1和f3可能会被银行b1实施抽贷行为,风险从渠道①和渠道③传导至企业f1和f3,所以企业f1和f3受到影响;因为银行b2和银行b1的拆借关系,风险从渠道②传导至银行b2,使其也受到影响,那么企业f1、f3和银行b2的权益也会受损。
图6(3):银行b2会将这种权益损失通过拆借和借贷关联传导至银行b1、b3和企业f2、f5(依次对应风险传播渠道④,⑦,⑧,⑩);企业f1会将这种权益损失通过借贷关系和担保关系传导至银行b1和企业f2(依次对应风险传播渠道⑤和⑩);同理,企业f3会将这种权益损失通过借贷关系和担保关系传导至银行b1和企业f5 (依次对应风险传播渠道⑥和⑪)。那么银行b1、b3和企业f2、f5的权益受损,且银行b1和企业f2、
 (1)
(1)  (2)
(2)  (3)
(3)  (4)
(4)
Figure 6. Steps of the risk contagion mechanism
图6. 风险传导机制的细化步骤图
f5多次受到风险的传导。
图6(4):银行b1会再次通过从渠道①、②、③将损失线性地传播给企业f1、银行b2和企业f3,那么企业f1、f3和银行b2的权益再次受损;同理,与银行b3有拆借和借贷关系的银行b2和企业f4、f6的权益受损;企业f2会将权益损失通过担保关系(渠道⑫、⑬)线性传播给企业f4、f1,通过借贷关系(渠道⑭)传播至银行b2,那么企业f1、f4和银行b2的权益受损。同理,与企业f5有担保和借贷关系的企业f3、f6和银行b2的权益也会受损。至此,风险通过各类关系传至系统中的各个节点,从而爆发系统性风险。
理论上风险扩散效应可以持续到系统内所有的个体破产,破产的表现之一是
。其实不仅仅只有信贷、担保和流动性风险造成危机,传播风险的渠道复杂多变,如支付系统、大量取款等,且具有共时性,加速危机银行权益资本的损耗,意味着现实中的金融系统性风险的爆发带来的影响很可能比本文所模拟的状况更为恶劣。当然,在过去的金融危机中,存在来自其他金融机构、政府、股东等的外部援助,在扭转财务困境中发挥了重要作用,因此只要得到及时救助,银行或企业仍然能够运营。
4. 基于银企间多层金融网络的模型思路分析
4.1. 对风险状态的测度思路
结合风险传导过程,本文期望在任意时刻测度个体和整体的风险状态。Debtrank算法的基本假设是损失从债务方线性地传播到债权方,债务方权益的贬值导致债权方资产同尺度的贬值,与本文分析的风险传导过程路径相吻合。在核算资产项变动的时候,我们依然沿用此假设。风险扩散可能造成债权方资产的潜在损失,债权人资产项目的变动与债务人权益变动情况有关。因而核算权益变动是测度风险中的重要环节:
对于银行的权益状态:
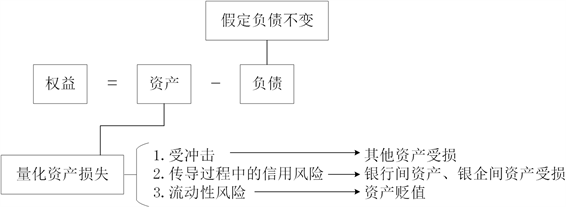
对于企业的权益状态:

4.2. 基于Debtrank算法的风险测度模型构建
在Debtrank算法中(Battiston等,2012 [39] ;Bardoscia等,2015 [40] ),测度任意时刻节点的风险状态有两个指标:一个是用以衡量节点i的脆弱性——
,其中
(下同),是一种相对指标;另一个是根据节点i的状态将节点分为三类——
,节点i在t时刻依次是“未遇险”,“传染”或“破产”三种状态之一。初始模型中的算法如下:
(1)
(2)
Debtrank算法是一种受反馈中心性启发的新颖度量方法,能够量化在外部冲击下,特定节点产生财务困境并将风险扩散至整个网络的程度。Battiston等(2012) [39] 将整个网络归一化,定义整个市场的总资
产为1;银行i的资产为
,即实际拥有的资产占整个市场总资产的比重;节点i对其直接邻居节点的影响
,与杠杆矩阵
以及其资产有关,对非相邻节点的影响为
,其中参数
是一个衰减因子;从而递归出
,用矩阵表示为
,可以解出
;Debtrank值由
给出,以此来反映
节点的相对重要性。目前已经有很多研究应用Debtrank算法来测度风险(Sebastian, 2015 [36] ; Silva, 2017 [41] ; Jing Ma, 2019 [42] )。
我们根据Bardoscia等(2015) [39] 对Debtrank改进中的一些方法和传导过程中的资产损失来推算权益,具体见公式(4)和(13);Debtrank算法不允许重复传染,即它只计算一次性传染,隔离了风险传染从节点i出发再返回到节点i的影响,因而计算出的影响力可能低于实际情况。而本文对于杠杆矩阵的假设放宽,
不再另
,而是根据相关节点是否破产分情况表示,具体见公式(5)和(14);损失是对于风
险测度的绝对性指标,而风险也是一种可能性,可以用相对值来表示,因而根据Debtrank算法分别测度银行和企业的H值,具体见公式(6)和(15)、(16);对于系统重要性节点的排序,具体见公式(9)和(19)。除了上文已经提及的冲击比例参数m,在此再引入新参数资产流动率
,用来反映市场流动性风险。
对于企业的风险测度模型思路:
(3)
(4)
(5)
(6)
(7)
(8)
(9)
对于银行的风险测度模型思路(其中
):
(10)
(11)
(12)
(13)
(14)
(15)
(16)
(17)
(18)
(19)
对于整体的风险测度思路:
根据公式(7)和(17),我们可以依次推断整个系统中企业和银行的节点状态,整体核算系统中处于“未遇险”,“传染”或“破产”三种状态的节点占比多少,以此判定系统性风险的宏观传染情况。
5. 结论
本文首先分析了金融网络系统中银行间同业拆借、银企间借贷和企业间担保三种关系,基于银行和企业这两类主体间的复杂关系,构建了多层网络,并基于银行和企业两类主体的资产负债表内及表外业务,阐述各主体间的债务债权关系;其次,本文从分层和分步两个角度分析了风险传导过程,对银行间市场、银企间市场和企业担保圈的风险链条式传染以及系统性风险的成因进行了解释;最后,基于Debtrank算法构建了风险测度的思路,分别提出对个体和整体的测度,以期能够使金融系统中的银行与实体经济体系中的企业更加深刻地体会宏观环境从而进行有利的经济行为,更为监管部门制定风险防范措施提供理论依据,从而提高金融风险政策调控效果。
基金项目
本文受到国家自然科学基金资助项目(71301078, 71472091, 71372181, 71171051, 71403131)、教育部人文社科青年基金项目(17YJC790002)、江苏省高校自然科学基金项目(13KJB120006)的支持。
NOTES
1通常担保分为一般担保和连带担保。当事人在保证合同中约定,债务方不能履行债务时,由保证方承担保证责任的,为一般保证。连带责任保证的债务方在主合同规定的债务履行期届满没有履行债务的,债权方可以要求债务方履行债务,也可以要求保证方在其保证范围内承担保证责任。如果保证合同中没有写明是哪种担保模式,则默认为是连带担保。