1. 问题分析
随着科技的发展,车联网技术被广泛的应用于交通车辆的安全管理中,车联网是指借助装载在车辆上的电子标签通过无线射频等识别技术,实现在信息网络平台上对所有车辆的属性信息和静、动态信息进行提取和有效利用,并根据不同的功能需求对所有车辆的运行状态进行有效的监管和提供综合服务的系统。当前道路运输行业等相关部门利用车联网等系统数据,开展道路运输过程安全管理的数据分析,以提高运输安全管理水平和运输效率。通过调查可知驾驶行为可能随气象、路况等因素的变化而变化,进一步影响行车安全、运输效率与节能水平。车辆的行车安全受到各方面因素的影响。
本文通过分析车辆行驶过程中的驾驶行为对行车安全、运输效率与节能情况的影响,运用数据挖掘的方法,综合考虑运输车辆的安全、效率和节能,并结合自然气象条件与道路状况等情况,通过分析多年份交通事故的主要导致因素以及各大重、特交通事故案列,同时结合气象条件和道路状况,可得到关于行车交通安全方面的几个重要指标:驾驶人因素,道路状况和交通环境。对各车辆交通运输过程中的费用消耗以及节能减排方面的相关法律法规,可以得到关于交通节能和效率方面的几个重要指标:驾驶人因素,道路状况和交通环境,工作车时利用率,运送速度,工作率等指标建立运输过程中的效率与节能评价标准指标体系,如图1所示:
2. 模型的建立
2.1. 模型的准备
为了综合考虑运输车辆的安全,节能,效率并结合自然气象条件和道路状况,选取合适的分析指标,利用模糊综合评价法对运输车车辆进行综合性评价。这种方法能有机地将评价对象定性和定量方法相结合,作出全面性,综合性和客观性的评价 [1] 。
2.2. 模型的建立
2.2.1. 行车安全指标体系的建立
为使一个有序的层次条理化,反映运输车辆运行安全因素的构成及内在的联系。结合我国车辆运行安全的实际特点,根据评价指标的系统性,相关性,完善性,适用性原则,应用层次分析法,建立递阶层次结构,如图2所示:
驾驶员因素
1) 运输车辆质量大,运输时间长,车速因素对交通安全有重要影响,一般运输车辆的限速为80 km/h,记车速超过限速的时间比例为:
式中T为道路上行驶得总时间,
为道路上超过限速的时间,
为车速超过限速的时间比例。
2) 车速标准差表现为速度的离散程度,车速分布得越离散,发生事故的概率越大,即为:
式中vm为车辆在道路上第m次采集的车速值;n为车辆在道路上采集到的车速样本量;va为车辆在道路上的车速平均值;vs为车辆在道路上的车速标准差。
3) 通过对方向盘转角的离散程度分析还可以对驾驶人的操控的稳定性进行评估。方向盘转角的离散程度可以用方向盘转角的标准差来判断:
其中
表示方向盘转角标准差;N表示所测得的方向盘转角样本数;
表示各测点得的方向盘转角值;
表示方向盘转角平均值。
道路状况因素
1) 平面线性与行车安全
长直线:根据统计分析的结果可知,当设计时速为100 km/h时,直线的长度上限应该控制在1500 m~2000 m;超过1500 m的直线段上潜的事故危险程度开始增大,超过2000 m时,危险性将快速上升,直线超过3000 m时,发生危险的概率将以线性规律的速度迅速上升。
短直线的过长或者过短对行车安全都不利,高速公路一次直线的最长度小于3分钟行程为安全,我国很多地区的一次直线长度都超过6km。短直线过短会对驾驶员造成一定的心理影响 [2] 。
当驾驶员行驶过第一个弯道到短直线上时,会按照刚刚的车辆行驶轨迹的曲率保持前轮的转弯角度,从而偏离轨道发生交通事故。
2) 平曲线
高速公路随着平曲线的半径减少,事故率会呈增加的趋势,最小半径可以用公式表示:
路面情况分析
1) 路面宽度与行车安全。总体来看事故率的发生于路面宽度基本是线性关系的,路面越窄,事故率越小
2) 中间带宽度与行车安全,根据已经统计的结果显示如表1:

Table 1. Situation after the separation belt is used
表1. 分隔带使用后的情况
通过表1可以看出随着宽度的增加,发生事故的概率是在减少的。
安全设施分析
1) 护栏与行车安全。半刚性护栏是通过车辆与护栏间的摩擦,车辆与地面间的摩擦,护栏产生一定的弹性变形来吸收碰撞能量,延长碰撞过程的作用时间。可以达到降低车速,使失控车辆改变行驶方向的效果,从而保证驾驶人的安全和安全事故发生的概率。
2) 防眩设施。防眩设施是指分布在中央分隔带上用于清除汽车前照灯夜间眩光影响的安全设施。他的分布根据地理条件等方面考虑,评价这个指标时可以按照防眩设施完备率,防眩高度和连续率等指标进行,防眩设施完备率用公式可以表示为:
其中r表示已布局的防眩设施,s表示应该布置的防眩设施。
3) 交通标志。在道路上的交通标志对驾驶员对道路的观察及时作出判断起到很大的作用。交通标志旨在通过对驾驶员适时,准确的诱导,充分发挥道路安全的效能。评价时可以按照标志完备率,限速标志最小间距率,不合理标志使用率,信息过载率等指标进行评价。
道路流量分析
道路上的人流和车流形成了交通流。交通量,速度,密度三个参数是描述交通流基本特征的主要参数。交通量指单位时间内通过某道路断面的交通体的数量,速度指区间平均车速,密度指单位长度道路区段上的车辆数量,此三参数之间的基本关系为:
式中Q表示平均车流量,V指区间平均车速,K表示平均密度。
根据学者统计的交通量与事故率的关系大致呈现U形关系,当交通量较小时,事故率比较高,随着交通量增大,比例逐渐下降,当等于0.6左右时,事故率又开始呈现逐渐增大的趋势。
交通环境因素
1) 雨雪雾天气分析
常见的冰冻风雪,雷暴大风以及能见度天气对交通有着至关重要的影响,根据文献已经采用过的方法,对不同气象条件下的道路交通事故发生率分析,采用主因子分析法,找到对道路安全影响较大的公因子。从总体因子分析数据来看,主要是日降水量,日均气温和能见度因子 [3] 。
降水量。降水量对道路安全的影响较为显著,对降水量分层分析,气象对道路安全的影响。当降水刚开始时,由于驾驶员的警惕性不高,并且道路的摩擦力减小,会增大交通事故的发生率。但是当有一定降水时,驾驶员的注意力会集中,减少交通事故发生的概率。由于数据不足,不能客观的评价不同降水量对道路安全的影响等级,故采用经验方式,结果如表2所示:

Table 2. Daily precipitation and risk level
表2. 日降水量与风险等级比重
平均气温。不同的气温对交通安全的影响是不同的,从长期的数据统计结果来看,在低温或者高温的条件下,人们的出行率降低,交通事故发生率相应的也会降低,当温度在[2, 12]时,事故发生率相对较高。结果如下表3所示:

Table 3. Stratified analysis of daily mean temperature
表3. 日平均气温的分层分析
能见度。能见度的影响不是大范围的区域也不是长时间的,故本文在选取能见度时采用一天中能见度最低时前后一个小时的均值,统计结果表明当能见度低于1 km时,交通事故率偏高,当能见度集中在[200, 500]时,发生交通事故的概率相对较高,日均最低能见分层分析结果如表4所示。

Table 4. Daily minimum visibility stratification analysis results
表4. 日最低能见度分层分析结果
逐步回归模型的建立
因子的挑选是逐步进行的,每一步挑选一个因子,要求所选出的因子是所有筛选因子之中能使残差平方和下降最多一个,且需要通过给定信度的显著性检验。假设第一步根据方差贡献大小选出因子x1,组成第一个过渡过程为:
其中
表示第一步方程的回归系数;再根据剩余因子的方差贡献大小挑选第二个因子,组成第二步过渡方程:
其中
表第二步方程的回归系数,然后根据同样的方法选出第三个因子,随着因子的逐步引入,由于因子之间的相互配合关系,可能出现显著性不强的的现象,若有这样的现象就剔除掉不显著的因子,得到最终效果的最佳拟合方程。
2.2.2. 节能指标体系的建立
1) 驾驶员操作。当驾驶员在行驶过程中反复出现怠速预热,空挡滑行,紧急制动,车速的不稳定性操作时。这在油耗上是一个很大的浪费。评价车辆是否节能时,可以当做驾驶员操作的评价指标。分别记录出现这些行为的次数S。
2) 环境温度和湿度的影响。和常温相比,当环境温度为−10度时,燃油消耗量增加高达45%。0度时的燃油消耗量增加了22%。而且湿度对燃油经济性的影响也很大,高于常温时,影响相对较少,高于0度时,湿度30%比湿度80%时节油15%。
3) 道路条件的影响。道路特征对运输车节能主要表现在各种路面条件下滚动阻力系数的差异。其中
Ff为滚动阻力,运输车质量一定,在不同的滚动阻力下行驶得油耗也是不同的。
2.2.3. 效率指标体系的建立
从时间,里程,速度,吨位等利用程度一系类指标的利用程度来反映运输车辆使用情况,主要可以从工作车车时利用率,运送速度,工作率三方面考虑
1) 工作车时利用率。统计车辆在线路上的行驶车时与线路工作车时之比,线路工作车时由行驶车时和线路上的停歇车时组成。即为:
2) 运送速度。车辆在运送时间内的平均速度,只计算起运点出发到终运点到达时刻。即为:
3) 工作率。统计期内工作日车与总车日之比,营运车辆一天内只要有工作即为一个工作车日。
步骤二:组合权重的确立
利用AHP-熵值法将客观和主观因素结合起来,采用组合权重法将所得到的结果综合起来,最终确定组合权重的大小 [4] ,权值wi的确定大小公式为:
其中
为AHP方法确定的权重大小。
为熵值法确定的权重大小。wi为组合权重的大小。
1) AHP法确定权重,如表5所示。

Table 5. AHP Method to determine the weight
表5. AHP法确定权重
为了得到各个因素准确的权重,需要构建判断矩阵。
根据特征根的值来确定权重的大小。首先求出判断矩阵的最大特征值,然后根据最大特征值计算判断矩阵的不一致程度指标为:
再查找相应的平均随机一致性指标,最后计算一致性比率:
若一致性比率小于1则有判断矩阵的不一致程度是可以接受的。
2) 熵值法确定权重的大小
在信息论中,熵是对不确定性的一种度量。信息量越大,不确定性就越小,熵也就越小;信息量越小,不确定性越大,熵也越大。根据熵的特性,可以通过计算熵值来判断一个事件的随机性及无序程度,也可以用熵值来判断某个指标的离散程度,指标的离散程度越大,该指标对综合评价的影响(权重)越大,其熵值越小 [5] 。
a) 选取n个评价对象,m个评价指标,则xij为第i辆运输车的第j个指标的数值其中
b) 指标的归一化处理:异质指标同质化
由于各项指标的计量单位并不统一,因此在用它们计算综合指标前,先要对它们进行标准化处理,由于正向指标和负向指标数值代表的含义不同(正向指标数值越高越好,负向指标数值越低越好),因此,对于高低指标我们用不同的算法进行数据标准化处理。其具体方法如下(分别是正向指标和负向指标):
为了方便起见,其中归一化后的数据为xij。
c) 计算第j项指标下第i辆运输车占该指标的比重:
d) 计算j项指标的熵值:
其中
e) 计算信息熵冗余度:
f) 计算各项指标的权值:
步骤三:模糊综合评价模型的建立
第一步:将对运输车的综合评价因素集U分为安全U1,节能U2,效率U3,每一级都满足这样的条
件分为
第二步:对每一个因素集Ui分别做出综合评价。设
为评语集,对每一个的权重分配
按照AHP-熵值法分配权重
若
为单因素评价矩阵,则得到一级评价向量:
第三步:将每个Ui看作一个因素,记为
每个ui作为U的一部分,同样可以按照权重分配
,得到二级评价向量:
同理可以往下不断划分,建立三级评价模型。
步骤四:建立评价准则
结合行车安全,节能已及效率三个方面,综合考虑气象条件以及道路状况,最后对运输车辆给出一个综合评价,合理的分析运输车辆在行驶过程中的不良驾驶行为 [6] ,综合评价的标准如表6。
3. 模型的求解
根据逐步回归模型结果如下图3可以看出日降水量,日平均气温与交通事故显著相关,显著水平SIG值均接近0,拟合效果可以。
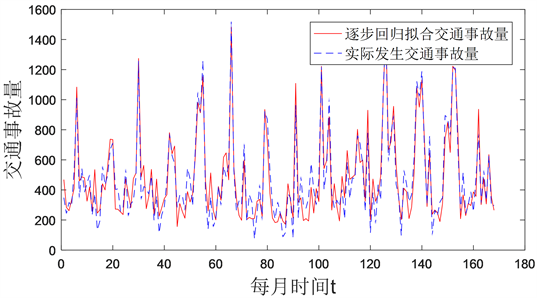
Figure 3. Actual recorded traffic accidents and fitting effects
图3. 实际记录的交通事故量与拟合效果图
从模型结果来看,降水量和交通事故量是显著正相关的,日均温度与交通事故量是显著负相关的,但是能见度和交通事故量的相关性不显著,最终得到了气象因子和交通事故量的未标准化系数下的逐步回归方程为:
根据AHP-熵值法结合主观和客观因素得到行车安全评价权重如表7所示:


Table 7. AHP-entropy method to determine weights
表7. AHP-熵值法确定权重
4. 结语
现如今随着科技的不断发展,行驶车辆的数量急剧增长,运输交通安全变得尤为重要,车辆的驾驶行为可能会随气象、路况等因素的变化而变化,从而进一步影响行车安全、运输效率与节能水平等。
通过本文建立的数学模型,从多方面的指标进行分析,例如:驾驶人因素,道路状况和交通环境,工作车时利用率,运送速度,工作率等,定性或者定量的分析各个因素对运输车辆行车安全行为的影响,通过建立逐步回归模型,得到各个因素与交通安全的关系,并拟合出函数关系方程。最后对车辆安全给出评价结果:优,良,一般,差。可以非常直观的得到车辆行驶过程中的驾驶行为对行车安全、运输效率与节能情况的影响。从而方便管理部门采取相应的措施来解决车辆行驶中的各种问题。