1. 引言
自D. Hilbert 16问题提出的一百多年以来,关于二维多项式微分系统的研究一直受到常微分方程专家学者们的高度重视并一直以来都是研究的热点,同时也获得了丰富的成果(见 [1] [2] )。但遗憾的是,该问题的研究距离完全解决还有非常遥远的距离,其中,即使对于二次、三次这样的低次幂多项式系统,至今也未能彻底解决。传统的方法采取通过做适当的变换将原方程化为一种特殊形式(liénard形式)之后再利用定性的方法讨论极限环的存在性。近年来,已有学者采用分支的方法研究了二次多项式微分系统的奇异环分支极限环以获得极限环的存在性条件(见 [3] [4] [5] [6] ), [7] 研究了Duffing方程的奇异环分支极限环问题, [8] 研究了软弹簧型方程在摄动下分支出极限环问题。本文作者将原方程化成一种特殊形式,再采用分支的方法对系统进行分析,来研究三次多项式系统的异宿环分支极限环的存在性问题,给出产生极限环的存在性条件和稳定性分析。
2. 预备知识
考虑平面自治系统
(2.1)
其中
,
。
2.1. 环域定理 [9] [10]
设由两条不相交的简单闭曲线
与
所围成的环形域D内及其边界上不含系统(2.1)的奇点,
与
均不是整条闭轨线,若平面自治系统(2.1)的凡与D的边界
相交的正半轨线均进入(均离开)环域D,则在D内至少存在此系统的一个内稳定(不稳定)的极限环和一个外稳定(不稳定)的极限环,二者可能重合为一。
与
称为环域的内外境界。
注1:环域定理的条件还可减弱,只要进入D的正(负)半轨不能跑出
也不能以
为
极限集,则结论照样成立。这种减弱意味着:1)
上可以有此系统的轨线段,但D的内或外境界线不能全由轨线构成;2)
上可以出现有限个奇点,只要保证轨线一旦进入(离开) D后不再离开(进入)即可。
注2:环域D的内境界线可以缩小成一个不稳定(稳定)的奇点。
注3:若D内仅存在唯一的闭轨线
,则
必是一稳定(不稳定)的极限环;若D内仅存在有限个闭轨,则逐个分析这些闭轨线的稳定性易知,D内至少有一个稳定(不稳定)的极限环;D内还有可能存在周期或复合极限环情形,但对解析系统这种情况不可能发生。
2.2. Melnikov函数 [11] [12]
考虑平面自治系统
(2.2)
及其扰动系统
(2.3)
其中
,
。
,
,
,
。假设
1) 系统(2.2)存在异宿于鞍点
和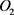 的两条异宿轨
和
构成的异宿环
,
为
,
上任意一点,过
作(2.2)的横截线l与
在
点的外法线方向
共线。
的两条异宿轨
和
构成的异宿环
,
为
,
上任意一点,过
作(2.2)的横截线l与
在
点的外法线方向
共线。
2) 扰动系统(2.3)在
和
点附近的鞍点分别为
和
,过
,
的稳定流形
和不稳定流形
与l的交点分别为
和
。
则在小扰动下,从
到
的有向距离
(
与
同向时为正)为:
(2.4)
其中,
为Melnikov函数。
3. 主要结果
考虑系统
(3.1)
通过定性分析可知系统(3.1)有鞍点
,鞍点
,另外,
为焦点(
)、或结点(
)、或中心型奇点(
)。(中心型奇点指中心或细焦点)。当
时 是稳定的,当
时
是不稳定的。
是稳定的,当
时
是不稳定的。
令
,
,
,
,
,则
,
,
与q同号,
。从而系统(3.1)化为:
(3.2)
令
,则系统(3.2)化为:
 (3.3)
(3.3)
考虑(3.3)的未扰系统
:
(3.4)
易知系统(3.4)有三个平衡点
、
和
。由线性变换的拓扑不变性,得到
和
为系统(3.4)的鞍点(如图1所示),
为中心型奇点,当
时
是稳定的,当
时
是不稳定的。
系统(3.4)为Hamilton系统,解得其首次积分为:
(3.5)
经简单计算可知,当
时,(3.5)为(3.4)的过鞍点
和鞍点
的异宿环,记为
,即
,其中
为
在v轴的右侧部分的异宿轨,
为
在v轴的左侧部分的异宿轨。由
知v的单调性,故
沿着
方向自下而上从
到
,
沿着
方向自上而下从
到
。即
为顺时针走向。
将
代入(3.5)得
。经分析可知,当
时,(3.5)为(3.4)的异宿环
内的一簇包围奇点
的闭轨,此亦说明
为(3.4)的中心。
下面我们讨论系统(3.3)在奇点
,
和
附近的轨线结构。
记
,
,
,
。
取
上一点
,不妨设此时
,即
,
,过
作
的截线
与
(
在
点的外法线方向)同向。设
与
分别为
经扰动破裂以后系统(3.3)过点
的稳定流形与过点
的不稳定流形,且
与
与
交点分别是
,
,由预备知识2.2中的Melnikov函数知,在扰动充分小的情况下,
到
点的有向距离为:
(3.6)
其中,
为沿着
的积分的Melnikov函数。
类似地,取
上一点
,不妨设此时
,即
,
,过
作
的截线
与
(
在
点的外法线方向)同向。设
与
分别为
经扰动破裂以后系统(3.3)过点
的稳定流形与过点
的不稳定流形(如图2所示),且
与
与
交点分别是
,
,由预备知识2.2中的Melnikov函数知,在扰动充分小的情况下,
到
点的有向距离为:
(3.7)
其中,
为沿着
的积分的Melnikov函数。
由(3.5)知
与
的表达式分别为
:
,
:
。由于
为逆时针走向。由(3.4)知
。则
又
,
,
,
,
,故
由于
,故而
与
同号。当
时,
,此时异宿轨
破裂以后稳定流形
在不稳定流形
的外部。当
时,
,此时异宿轨
破裂以后稳定流形
在不稳定流形
的内部。
类似地可以得到,
又
,
,
,
,
,故
由于
,故而
与
同号。当
时,
,此时异宿轨
破裂以后稳定流形
在不稳定流形
的外部。当
时,
,此时异宿轨
破裂以后稳定流形
在不稳定流形
的内部。
下面,我们要证明极限环的存在性,利用预备知识2.1环域定理,只需构造所需的内外境界即可。
首先,当
(即
),
为系统(3.3)的不稳定的结点
或焦点
,因此可取
作为环域定理所要求的环域D的内境界。
其次,我们选取
作为环域D的外境界。由前面分析得知,当
时,
,此时异宿轨
破裂以后稳定流形
在不稳定流形
的外部,当
时,
,此时异宿轨
破裂以后稳定流形
在不稳定流形
的外
部。并且当系统(3.3)的轨线穿过线段
时均沿自下而上的方向穿过进入D。当系统(3.3) 的轨线穿过线段
时均沿自上而下的方向穿过进入D。同时(3.3)满足解的存在唯一条件,所以,由Poincare-Bendixson环域定理得,此时在环域定理D中系统(3.3)至少存在一个稳定的极限环。
其它情况类似可证明。于是我们得到:
定理:1) 当
(即
)且
,
时,系统(3.3)在
的邻域内至少存在一条围绕
的稳定极限环。
2) 当
(即
)且
,
时,系统(3.3)在
的邻域内至少存在一条围绕
的不稳定极限环。
基金项目
山东省自然科学基金(ZR2018MA016, ZR2015AL005),山东省软科学研究计划项目(2012RKA13021),临沂大学大学生创新创业训练计划项目(201710452001)。
NOTES
*通讯作者。