1. 引言与主要结论
Euler函数φ(n)是数论中非常重要而有意义的一类函数,定义为
中与n互素的个数。为了将Lehmer同余式从模素数的平方推广到模任意整数的平方,蔡天新 [1] 等对广义Euler函数的作出了如下定义。
定义:广义欧拉函数φe(n)
(1.1)
即序列
中与n互素的数的个数。显然,当e = 1时,广义欧拉函数φe(n)就是欧拉函数φ(n)。
当e = 2时,由广义欧拉函数定义,容易验证,
,
,对
,有
(1.2)
关于Euler函数φ(n)以及广义Euler函数φe(n)的性质以及与广义Euler函数相关的数论方程的研究非常活跃。文献 [2] [3] 对广义Euler函数的性质有一定的研究。同时,对于包含广义Euler函数的方程也有所讨论,如文献 [4] - [14] 对包含广义Euler函数φe(n)以及ω(n)和Ω(n)的方程的可解性;文献 [15] [16] [17] [18]
讨论了形如
方程的可解性;文献 [19] [20] 对包含Euler函数和广义Euler函数的方程的正整数解进行了研究;文献 [21] - [28] 给出了形如
,
这种形式的方程的可解性。
本文将研究更一般的方程,即方程
(1.3)
(1.4)
以及
(1.5)
的可解性,其中
是给定的素数。求出了一些方程的全部解,并获得了一些一般性的结论。本文的主要结论是:
定理1:方程(1.3)的所有非负整数解(m, x, y) (表1所示)为

Table 1. All nonnegative integer solutions of Equation (1.3) (m, x, y)
表1. 方程(1.3)的所有非负整数解(m, x, y)
定理2:方程(1.4)的所有非负整数解(m, x, y) (表2和表3所示)为
1) 若
时,
,有

Table 2. In the case of p = 2, q > 5, the nonnegative integer solutions of Equation (1.4) (m, x, y)
表2. 在p = 2,q > 5的情况下,方程(1.4)的非负整数解(m, x, y)
2) 若
,
,即
,有

Table 3. In the case of p, q ≥ 5, the nonnegative integer solutions of Equation (1.4) (m, x, y)
表3. 在p,q ≥ 5的情况下,方程(1.4)的非负整数解(m, x, y)
定理3:方程(1.5)的解(m, x, y)满足
1)
,当
(
)时,
,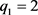 ,
(
),且
(
)。
,
(
),且
(
)。
2)
,必有
,
,
,其中
,则
,且
,
。
2. 方程φ2(m) = 2x3y的解
本节讨论方程(1.3)的解,由于
,
故令
其中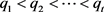 且均为质数,则
且均为质数,则
(2.1)
2.1. 情况1:t = 1
当
时,有
(2.2)
情况1.1:当
时,可得
,
(
),故
,
。
情况1.2:当
时, 。
。
情况1.2.1:当
时,
,可得
(
),
(
),故
,
。
情况1.2.2:当
时,
,可得
(
),
(
),故
,
。
2.2. 情况2:t = 2
当
时,有
(2.3)
情况2.1:当
时,有
,可得
,
,
(
;
)。故
,
。
情况2.2:当
,
时,有
。
情况2.2.1:当
,
(
,且为质数)时,
,可得
(
),
(
),
(
),故
,
。
情况2.2.2:当
,
(
,且为质数)时,
,可得
(
),
(
),
(
),故
,
。
情况2.3:当 ,
时,有
。
,
时,有
。
当
,
时,
,可得
(
),
(
),
(
)。故
,
。
2.3. 情况3:当t ≥ 3时,有
(2.4)
情况3.1:当
(
)时,有
可得,
,
(
),故
,
。
情况3.2:当
,
(
)时,有
。
情况3.2.1:当
,
(
且为质数,
)时
,则可得
,
(
),故
,
。
情况3.2.2:当
,
(
且为质数,
)时,
,可得
,
(
),故
,
,
,
。
情况3.3:当
,
,
(
)时,有
。
情况3.3.1:当
,
,
(
且为质数,
)时,
,可得
,
(
),故
,
,当
时,
。
于是定理1得证。
3. 方程
的解
本节将在定理1:
的解的情况的基础上,对更一般的情况来作进一步的讨论,即
(其中p,q为质数,且)。当
,
时,与定理1相同,下面,我们讨论
,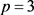 不同时成立的情况。
不同时成立的情况。
3.1. 情况A
,
,
,则
(3.1)
同样地,我们设
其中
且均为质数。
情况1:t = 1当
时,
。
情况1.1:当
时,
,
(
),故
,
(当
时,
;
时,
)。
情况1.2:当 时,
。
时,
。
情况1.2.1:当
时,
,可得
(
),
(
),故
,
。
情况1.2.2:当
时,
,可得
(
),
(
),故
,
。
情况2:t = 2当
时,
。
情况2.1:当
时,有
,可得
,
,
(
;
),故
,
。
情况2.2:当
,
时,有
。
情况2.2.1:当
(
,且为质数)时,
,可得
(
),
(
),
(
),故
,
。
情况2.2.2:当
时,(
,且为质数)
,可得
(
),
(
),
( ),故
,
。
),故
,
。
情况2.3:当
,
时,有
,此时必定有
,则有
(
),
(
),
(
),故
,
。
情况2.4:当
,
时,有
。
当
,
时,
,可得
(
),
(
),
(
),故
,
。
情况3:t = 3当t = 3时,
。
情况3.1:当
时,有
,可得
,
(
),
,
(
)
当 时,必有
且
,故
,
。
时,必有
且
,故
,
。
情况3.2:当
,
时,有
。
情况3.2.1:当
时,
,可得
(
)。
(
),
,
(
),
当
时,必有
且
,故
,
。
情况3.2.2:当
时,(
,且为质数)
,可得
(
),
(
)当
时,必有
,
,
(
),
且
,故
,
。
情况3.3:当
,
,
时,有
,可得
(
),
(
),
(
),
(
)且 ,故
,
。
,故
,
。
情况3.4:当
,
时,有
。
则
,可得
(
),
(
),
(
),
(
)且
,故
,
。
情况3.5:当
,
,
时,有
。
则
,
(
,且为质数)时,
,可得,
(
),
(
),
(
)当
时,必有
,
(
)当
时,必有
且
,故
,
。
情况4:
时,
。
情况4.1:当
(
)时,有
可得
,
(
),故
,
。
情况4.2:当
,
(
)时,有
。
情况4.2.1:当
,
(
且为质数,
)时,
,可得
,
(
),故
,
。
情况4.2.2:当
(
且为质数,
)时,
,可得
,
(
),当
时,
,故
,
。
情况4.3:当
,
(
)时,有
。
当
(
且为质数,
)时,
,可得
,
(
),当
时,
,故
,
。
情况4.4:当
,
,
(
)时,有
。
情况4.4.1:当
,
,
(
且为质数,
)时,
,可得
,
(
),故
,
。其中
,
不能同时取。
3.2. 情况B
由于当
时,必有
,与定理1相同,故下面讨论
,
时的情况
当
,
时,
,
,则
(3.2)
情况1:t = 1:当
时,
情况1.1:当
时,
,
(
),故
,
(当
时,
;
时,
)。
情况1.2:当
时,
。通过分析易知
,则
或者
。
情况1.2.1:当
时,
,可得
,
(
),此时只有在
下有解。
(
),故
,
。
情况1.2.2:当
时,
,可得
(
),
(
),故
,
。
情况2:t = 2当
时,
。
情况2.1:当
时,有
,由于
,易知
,
方程不成立,无解。
情况2.2:当
,
时,有
,无解。
情况2.3:当
,
时,有
,无解。
情况2.4:当
,
时,有
,无解。
情况3:t ≥ 3当
时,
,无解。
于是定理2得证。
4. 方程
的解
本节将在前面两个定理的基础上,延申到更加一般的情况:即
(令
且均为质数),由分析知,必有
。则
(
)。由
,其中
且均为质数,则可得,
(4.1)
其中必有
,因为当
时,方程(4.1)无解。
4.1. 情况1
当
时,
(令
)
情况1.1.1:当
时,由
,可得
,
(其中
),
,
,
,
。
情况1.1.2:当
时,由
,易知
,
,可得
,
,
(其中
,且不包含
这一素数),
,
,
(
)
之后也为0。
4.2. 情况2
当
时,
(令
)
情况2.1.1:当
时,由
,可得
,
,
,
,
,
。
情况2.1.2:当
,
时,有
,当
时,
,可得
(
),
,
,
,
,其中
,
(
)
之后也为0。
情况2.1.3:当
,
时,由
,易知
,可得
,
,
,
,
,
,
(
)
之后也为0,
(
)
之后也为0。
4.3. 情况3
当
时,
。
情况3.1.1:当
时,由
,可得
,
,
,
,
。
情况2.1.2:当
,
时,有
,当
时,
,可得
(
),
,
,
,
,
(
),
之后也为0。
情况2.1.3:当
,
,
时,由
,易知
,
,可得
(
),
,
,
,
,
(
)
之后也为0。
(
)
之后也为0。
情况2.1.4:当
,
,
,
时,由
,易知
,可得
(
),
,
,
,
,
(
),
之后也为0。
(
),
之后也为0。
(
)
之后也为0。
由此可得,当
时,
。
将以上讨论概括为以下两个情况:
情况1:
,当
(
)时,
,
,
(
),且
(
)。
情况2:
,必有
,
,
,其中
,则
,且
,
。
于是定理3得证。
致谢
作者衷心感谢阿坝师范学院杨仕椿教授的悉心指导与无私教诲!
基金项目
全国大学生创新训练项目(201810646012),阿坝师范学院教学科研项目(201805087, 20170203, 20171510, 20171515)。