1. 引言
用水效率是我国实行最严格水资源管理制度的核心内容之一,我国现状水资源利用效率较发达国家相比仍有一定差距。因此,水资源利用效率的研究对划定用水效率红线、改善用水现状等具有重要的指导意义。
水资源利用效率评价是一个涉及多层次、多目标的问题。近年来的相关研究已经取得了一些进展,如李红新 [1] 、张旭腾等 [2] 、朱燕飞等 [3] 运用了数据包络分析(DEA)模型在水资源利用效率评价中;王晓琳等 [4] 基于物元可拓模型对江西省2011~2014年的用水效率进行了评价;孟令爽等 [5] 使用主成分分析法对上海市2008~2015年的用水效率做出评价;段长桂等 [6] 基于迭代思想的水资源利用效率评价模型分析了山东省2014年17个地区的用水效率并进行排序;余兴奎等 [7] 采用模糊层次分析法评价了云南省的水资源利用效率;朱兆珍等 [8] 通过突变级数法对我国31个省的水资源利用效率进行评估并对其进行聚类分析;李恩宽等 [9] 利用投影寻踪模型对黄河流域水资源利用效率进行评价;管新建等 [10] 搭建了CRITIC-TOPSIS-灰色关联评估模型对淮河流域2011~2016年的用水效率进行了评价。
灰靶模型在解决多层次、模糊的决策问题时,具有一定优势 [11] 。该模型自提出以来已被广泛应用于土地生态安全评价 [12] 、适宜性评价 [13] 、生态环境影响评价 [14] 等方面,但在水资源评价领域应用较少且传统灰靶模型存在等权问题需要加一改进。鉴于此,本文构建了涵盖综合、工业、农业、生活、生态环境这5大方面的水资源利用效率评价指标体系,引入了CRITIC客观赋权法,弥补了传统灰靶模型中等权的不足,建立了基于CRITIC权的改进灰靶模型。以郑州市为研究区进行水资源利用效率评价,同时利用障碍因子诊断模型来识别影响水资源利用效率的障碍因素,以期探索新方法在水资源利用效率方面的应用价值,为提升水资源利用效率提供科学依据。
2. 区域概况及评价指标体系
2.1. 研究区域概况
郑州市是河南省省会,位于黄河中下游,地处华北平原南部,跨黄河、淮河两大水系,介于东经112˚42'~114˚14'、北纬34˚16'~34˚58'之间,是我国中部地区重要的中心城市,辖4市1县3区(不含巩义市),总面积6470.3 km2,地势整体呈现东北低、西南高的趋势。郑州市多年平均降水量640.5 mm,全市降雨时程分配严重不均,主要集中在7、8、9月。郑州市多年平均水资源总量11.2578亿m3 (2017年郑州市水资源公报),人均水资源占有量为124.4 m3,是水资源严重短缺的城市。
2.2. 评价指标体系及数据来源
杨丽英等 [15] 对水资源效率评价指标体系进行深入探讨发现,与水资源利用效率相关联的指标众多,在应用时不能进行全部罗列且数据可获得程度不同。故本文在进行遴选指标时遵循动态性、科学性、代表性的原则,结合数据收集难易程度,依据《郑州市水资源公报》中主要的用水指标,构建了同时涵盖工业、农业、生活、生态环境、综合这5大方面7项指标的郑州市水资源利用效率评价指标体系,见表1。在当前情形下,郑州市持续推进水生态文明城市建设,成效显著,故在指标体系构建时选取了生态环境用水比例和污径比作为生态环境用水指标。文中的数据来源于《郑州市水资源公报》(2017年)。

Table 1. Zhengzhou City water resources utilization efficiency evaluation index system and index weight value
表1. 郑州市水资源利用效率评价指标体系及指标权重值
3. 研究方法
3.1. 改进的CRITIC赋权法
CRITIC赋权法由Diakoulaki提出的一种新型客观赋权方法,以指标特征的对比强度和冲突性来综合反映指标的客观权重,它不仅考虑指标内部的变异程度,而且还考虑了指标之间的冲突性,充分考虑了指标的内部和外部特性,赋权结果更为客观、合理。传统的CRITIC赋权法存在下列两方面的不足:第一,带量纲的标准差无法反映出指标内部的对比强度大小;第二,出现负相关时,用相关系数反映指标冲突性显然不合理,参考王瑛等 [16] 的研究成果,利用变异系数和带绝对值的Pearson相关系数对传统CRITIC赋权法进行改进,则改进后的赋权公式为:
(1)
因此,第j个指标的客观权重wj表示为:
(2)
式中:Cj为信息量;δj为第j个指标的变异系数,用指标标准差与均值的比值表示;rij表示第i个评价指标与第j个评价指标的相关系数。
3.2. 改进的灰靶模型
灰靶模型的原理是在缺乏统一标准的基础上,构造一个灰靶,并在其中找到靶心将其设定为标准,然后通过比较待评方案与标准方案来计算靶心度,进而划分等级标准,详细步骤见文献 [11] 。由于传统灰靶模型采用等权重计算靶心度,与实际不符。本文将改进后的CRITIC客观赋权法引入到靶心度计算公式中,改进后的灰靶模型靶心度计算公式为:
(3)
(4)
式中:
、
分别表示待评方案xi相对于标准方案的靶心系数和靶心度值。通常情况下,分辨系数ρ = 0.5。
3.3. 水资源利用效率障碍因子诊断模型
引入因子贡献度(即权重wj)、指标偏度Ij (即各指标标准化后的实际值与最优值之间的差,可用灰差异信息空间值Δ表示)及障碍度Mj (Mj值的大小表示各指标或准则层指标对区域水资源利用效率影响程度的高低) 3个指标,对影响水资源利用效率的主要障碍因素进行分析与诊断。障碍度计算公式如下:
(5)
4. 郑州市水资源利用效率评价
4.1. 郑州市水资源利用效率评价过程
以2017年郑州市的8个地区为待评方案X1~X8,将表中各指标通过式(1)~(2)计算得到各指标的权重值wj。在原始数据uij中找到靶心将其设定为标准,再利用灰靶变换公式得到灰靶变换值vij,结果见表2;构造灰关联差异信息空间矩阵Δvij并利用式(3)~(4)计算靶心系数γij及靶心度,见表3;依据上述求得靶心度φi的取值,采用自然断点法将其均匀划分为5个评价等级。因靶心度φi值大多在0.4~0.6之间,故等级标准划分结果见表4。

Table 2. Actual value of indicator data and gray target transformation result
表2. 指标数据实际值及灰靶变换结果

Table 3. Grey relation difference information space and bull's-eye coefficient, bull's-eye value
表3. 灰关联差异信息空间及靶心系数、靶心度值

Table 4. Results of classification criteria by natural breakpoint method
表4. 自然断点法划分等级标准结果
利用公式(5)计算得到郑州市水资源利用效率各指标的障碍度,由于指标众多且障碍度大小不一,仅筛选出障碍度值较大的指标作为影响郑州市水资源利用效率的主要障碍因素,各地区主要障碍因子及障碍度见图1。
4.2. 评价结果
由表3数据可知,郑州市各地区水资源利用效率的高低排序及等级依次为:郑州市区 > I级 > 中牟县 > 上街区 > II级 > 荥阳市 > III级 > 新郑市 > 航空港区 > 新密市 > 登封市 > IV级。通过与TOPSIS法的进行比较,两种方法得到的结果具有较好的一致性,见表5,表明将灰靶模型应用到郑州市水资源利用效率评价中是可行的。
通过对郑州市水资源利用效率的主要障碍因素及障碍度进行分析,识别出水资源利用效率的主要障碍因素是生态环境指标中生态环境用水比例,其次是污径比。

Table 5. Evaluation results of water resources utilization efficiency in Zhengzhou City
表5. 不同评价方法计算结果对比
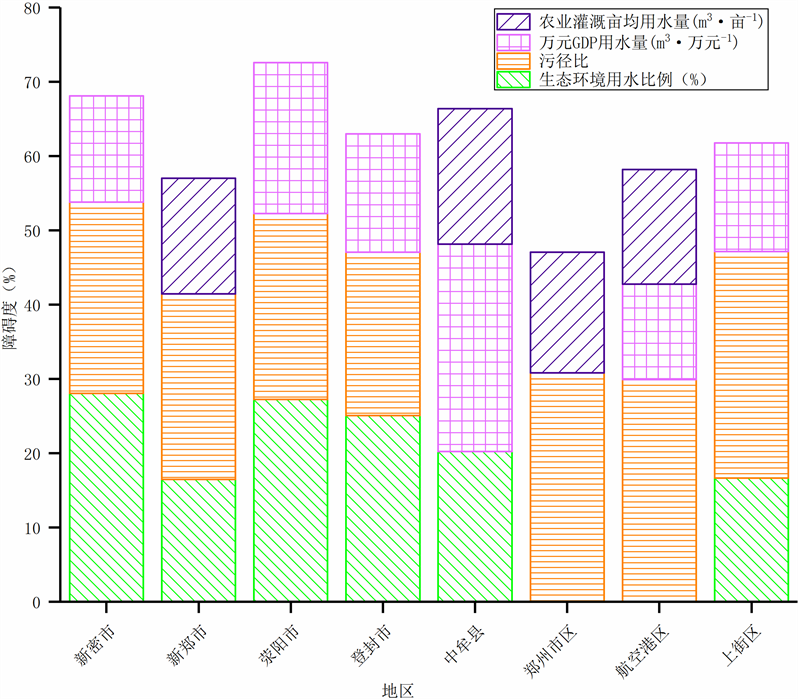
Figure 1. Main obstacle factors and obstacles of water resources utilization efficiency in Zhengzhou City
图1. 郑州市水资源利用效率主要障碍因子及障碍度
5. 结论
将CRITIC客观赋权法引入到灰靶模型中,克服了传统模型的不足,构建了基于CRITIC权的改进灰靶模型,通过采用不同方法对郑州市水资源利用效率评价结果比较,两种方法得到的结果具有较好的一致性,表明了改进灰靶模型在水资源评价中的应用价值,利用障碍因子诊断模型识别了阻碍郑州市各地区水资源利用效率的主要障碍因子。
基金项目
国家自然科学基金项目(51509088, 51709108);河南省高校科技创新团队(14IRTSTHN028);河南省水环境模拟与治理重点实验室(2017016)。