1. 引言
在实际应用中,我们常常对总体进行某种分布的假设,抽样得到样本信息,去估计总体参数,这种方法称为参数估计方法。但当对总体信息一无所知,或不假定总体分布形式,只通过样本信息对总体参数进行估计,此时,非参数估计就展现了很强的灵活性。
非参数回归分为局部回归、光滑样条回归、正交回归。光滑样条回归,因其在抽取样本对总体进行回归时,不必依赖总体分布形式,在减小误差、提高预测精确度、提高拟合曲线的光滑度上都体现了良好的特性。
在诸多方法中,三次光滑样条因其计算简便、结果有良好的统计性质而应用广泛。在光滑样条的学术研究上,陈长生、徐勇勇(1997)主要重点研究了儿童成长曲线的光滑样条拟合 [1] ,回归结果优于参数估计方法。2000年其在此基础上进行加权光滑样条的改进 [2] ,改进后模型效果更好,稳定性更强。卢一强、陈中威(2010)主要研究了基于光滑样条的选择方法,提出了部分线性模型中的非参数函数部分的假设检验是否为多项式的假设检验方法 [3] 。本文通过介绍光滑样条回归模型、算法、案例分析,基于R语言的实现,对光滑样条进行研究以及光滑样条回归与多项式回归结果的比较分析。
2. 理论模型及方法论
2.1. 非参数回归模型的一般形式及模型
设Y为因变量
为自变量,非参数回归模型的一般形式为
其中对p元回归函数只作一些连续性或光滑性的要求。由于非参数回归模型不假定回归函的具体形式而增加了模型的灵活性和适应性。
设
Math_12#为来自总体
的一个样本容量为n的独立同分布的样本,需要基于观测值
Math_15#估计
并进行有关的统计推断。
非参数回归的模型为:
数据和模型是统计分析的两个信息来源,数据带有“噪声”,但无偏,而模型实际上是种约束,有助于降低噪声,是响应的。在“偏差–方差”的平衡表上,代表两个极值的分别是标准参数模型和无约束非参数模型。在两个极值之间,存在着大量的非参数或半参数模型,其中大多数被称为平滑方法。非参数估计族可通过惩罚似然法导出各种随机环境下的模型 [4] 。
2.2. 三次平滑模型样条
光滑样条回归实际上是一种局部建模方法,是按照一定的光滑性连接起来的分段多项式 [3] 。首先先介绍多项式样条回归估计,多项式样条估计的最小化式为:
在实际生活中,三阶样条比较常用,原理如下:
设某区间
上有实数
且满足
,
是定义在区间
的函数,如
满足以下条件[儿童参考]:
1) 在
上,函数
为三次多项式。
2) 函数
及其二阶导数在
处处连续。
则称这样的分段多项式函数为三次样条函数,
为样条函数的节点。令
,
,
为三次光滑样条的表达式。光滑样条估计的基本思想是寻找一个光滑函数使得残差平方和最小,所以引入惩罚函数,使得惩罚平方和最小,估计方法为惩罚最小二乘估计,表达式为:
损失函数
是使
能很好的拟合数据,而
则对函数
的波动性进行惩罚,二
阶导数
对应了斜率的变化程度,衡量的是函数的粗糙度。
为需要选择的光滑参数也称拉格朗日乘子,此方法可以避免多项式样条估计的节点选择对非参数拟合曲线的光滑程度影响。
值越大,函数
越光滑。
3. 光滑样条基本算法
1) 目标函数均方误差最小
2) 写成矩阵形式,其中
其中
,
。
3) 运用最小二乘法估计
4) 带入拟合函数
设B为N*M的矩阵,
5) 求光滑参数
矩阵
可以写成
此时
矩阵S具有对称半定性质,对其进行特征分解:
其中,
,这里的
是矩阵K的特征值
6) 估计样条函数
4. 基于R语言的随机模拟比较研究
光滑样条的拟合用R语言的smoothing.spline()实现。随机模拟实验运用R语言,随机生成变量X,Y,运用光滑样条方法回归拟合X与Y之间的关系。
#模拟实验
>set.seed(1)
>ei<-rnorm(4000,0,3) #生成均值为0,标准差为1的4000条残差序列
>x<-rnorm(4000,1,0.5) #生成均值为1,标准差为0.5的4000条x序列
>y<-5*x^2+*x^3+ei #设置x、y关系式,生成y
>plot(x,y,cex=.8,col=darkgrey) #画出x、y的散点图
>title(Smoothing Spline) #题头命名“光滑样条”
>fit=smooth.spline(x,y,df=10) #设置初始自由度为10,进行光滑样条拟合
>fit2=smooth.spline(x,y,cv=TRUE)#运用交叉验证法,调整自由度,再次利用光滑样条拟合
>fit2$df
[1] 9.793812 #读出调整的自由度值为9.79
>fit2$lambda
[1] 0.004389605##读出调整的光滑参数为0.0044
>lines(fit2,col=blue,lwd=2) #画出光滑样条曲线
>attr(bs(x,df=9.8)knots)#读出自由度为9.8时,样条结点的位置
12.5% 25% 7.5% 50% 62.5% 75%100%
0.4115038 0.6566871 0.8289012 0.9908485 1.1491730 1.3207943 2.8121807
运用光滑样条方法拟合的图形如图1所示。
5. 实证分析
本文以R语言中ISLR包中Wage数据集为例,此数据集是以美国中部大西洋地区男员工收入水平为背景的调查数据,通过此数据集运用多项式回归和光滑样条回归两种方法分析比较研究工资水平和年龄之间的关系。
#R语言加载ISLR包,调出数据集,进行数据可视化(如图2)
>library(ISLR)
>attach(Wage)
>plot(age,wage,xlim=agelims,cex=.5,col=darkgrey)
5.1. 多项式回归模型
由wage-age的散点图可以,两变量之间不存在线性关系,最好是拟合一条曲线,使散点均匀地散落在曲线两侧,首先尝试构造多项式回归模型。构造多项式回归模型时,应该在足以解释自变量和因变量关系的前提下,回归次数越低越好,避免变量间产生多重共线性。运用交叉验证法选择合适的多项式次数。
#运用交叉验证法选择多项次最佳回归次数
>nrow(Wage)
[1] 3000
>train = sample(1:3000,2000)
>cv.err = vector(numeric,5)
>for(i in 1:5){
+ fit = lm(wage~poly(age,i),data = Wage,subset = train)
+ pred = predict(fit,newdata=Wage[-train,])
+ cv.err[i] = mean((pred-wage[-train])^2)
+}
>plot(1:5,cv.err,type=l)
图3为交叉验证的结果图,横轴表示多项式的次数,纵轴表示均方误差,从图中可以看出,多项式次数为4、5时,均方误差较小,考虑到模型的简单化,多项式回归次数得到最佳选择是4次。
#构造4次多项式回归模型
>fit = lm(wage~poly(age,4),data = Wage)
>agelims = range(age)
>age.grid = seq(from=agelims[1],to=agelims[2])
>preds = predict(fit,newdata = list(age=age.grid),se=T)
>se.bands=cbind(preds$fit+2*preds$se.fit,preds$fit-2*preds$se.fit)# 构建预测值的置信区间
>plot(age,wage,xlim=agelims,cex=0.5,col=darkgrey)
>title(Degree-4 Polynomial,outer = T)
>lines(age.grid,preds$fit,lwd=2,col=blue) # 多项式回归预测曲线
>matlines(age.grid,se.bands,lwd=2,col = red,lty=3) # 置信区间曲线
图4中,红色虚线代表置信区间曲线,由拟合的图形可以看出,拟合的效果还不错。
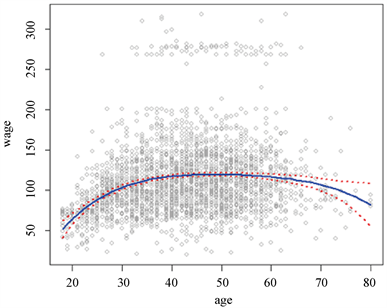
Figure 4. Degree-4 polynomial regression
图4. 4次多项式回归
#方差分析
> anova(fit)Analysis of Variance Table
Response: wage
Df Sum Sq Mean Sq F value Pr(>F)
poly(age, 4) 4 450482 112620 70.689 <2.2e−16 ***
Residuals 2995 4771604 1593
---
Signif. codes:0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
方差分析结果中,F值较大,回归模型显著,同样说明4次多项式回归拟合Wage-age的关系效果良好。
5.2. 光滑样条回归
光滑样条的拟合用R语言的smoothing.spline()实现。和多项式回归要确定次数一样,光滑样条回归的关键是要确定样条结点的个数、位置和光滑参数。
#光滑样条回归
>plot(age,wage,xlim=agelims,cex=.8,col=darkgrey)
>title(Smoothing Spline)
>fit=smooth.spline(age,wage,df=18)#第一次设定自由度为18
>fit2=smooth.spline(age,wage,cv=TRUE)#交叉验证法调整自由度
>fit2$df
[1] 6.794596#调整后的自由度为6.7946
>lines(fit,col=red,lwd=2)
>lines(fit2,col=blue,lwd=2)
>legend(topright,legend=c(18 DF6.8 DF),col=c(redblue),lty=1,lwd=2,cex=.8)
此段代码中进行了两次拟合,使用了两次smoothing.spline()函数,第一次设定初始自由度df = 18,此时函数值确定自由度df为18对应的光滑参数λ的值。第二次调整,迭代计算,通过交叉验证选择合适的值,最终结果就是由λ值选出的自由度为6.7946。
> library(splines, lib.loc=F:/R-3.5.1/library)
> attr(bs(age,df=6.7946)knots)#样条结点位置
20%40%60% 100%
32 39 46 80
经光滑参数选出df = 6.7946的样条回归模型中,R语言给出的样条结点为32、39、46、80。下图是分别为自由度为18和6.8的回归样条。
从图5中可以看出,自由度为6.8的样条(蓝线)比自由度为18的样条(红线)要光滑的多。这就是光滑参数起到了重要作用。
5.3. 多项式回归与光滑样条比较
图6中,绿线是4次多项式的拟合曲线,蓝线是利用光滑样条拟合的曲线,在题中,两者的拟合效果均较好,拟合曲线相差不大,图中头尾两部分可以看出,采用光滑样条拟合的曲线在首尾两端较多项式拟合的曲线平稳,结合图上散点的位置,得出光滑样条回归拟合的结果要优于多项式回归的结果。
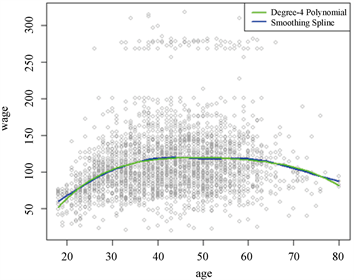
Figure 6. Degree-4 polynomial VS smoothing spline
图6. 4次多项式 VS 光滑样条
6. 结论
基于美国中部大西洋地区男员工收入水平数据,通过实证分析,可以得出结论如下:
工资会随着年龄的增长呈先上升后下降的趋势;人从20岁开始工作到40岁收入是上升的,此阶段事业处于上升期,工资水平的增速是缓慢下降的;40岁到60岁工资的水平趋于平稳;60岁之后工资水平缓慢下降。从图中可以看出60岁到80岁收入水平虽然在下降,依然处于较高的水平,这和美国的退休制度有关系,美国政府没有硬性规定的统一退休年龄,工薪族往往依照自己的身体和财务状况作出选择,可以选择提前退休或正常退休。基本上在美国65岁被普遍认为是一个正常的退休年龄,图中在65岁左右的高、中、低的收入分布较40~60岁阶段没有显著变化。美国实行的是一个“弹性退休制度”,所以在美国经常还有年纪大的老人坚持工作,这一点不同于中国,我国有明确的法定退休年龄,男性60岁,女性50岁。
从回归拟合的结果角度看,光滑样条的拟合要优于多项式的拟合。惩罚平方和综合考虑了曲线拟合的两个方面:拟合优度和光滑度。同时光滑样条回归不必事先对结点进行选择,克服了以往利用样条函数进行曲线拟合时存在的缺点,避免了结点选择的盲目性,既提高拟合程度又在一定程度保证曲线光滑,使得拟合曲线精确美观。非参数回归应用广泛,使用性强,它所需要假定比参数回归弱的多,适用任何分布的数据,尤其当反应变量与解释变量间函数关系不清楚时,参数模型难以进行拟合处理,此时非参数估计可作为拟合曲线的一个非常有效的方法。