1. 引言
云计算 [1] [2] 可以为人们或中小企业以即用即付的方式提供便捷的计算能力和存储资源,具有减少设备维护开销、快速部署、支持动态资源调整等优势。越来越多的个人和企业将数据存储和计算任务外包到云服务器上完成,然而外包过程会导致用户私有数据泄漏给云服务器,其中可能包含个人健康状况、收入、企业用户数据等隐私信息和私密数据。外部入侵或者内部不诚实员工偷盗数据等因素都可能导致云服务器上的数据发生严重的泄漏。此外,云服务器可能因为软硬件错误或者主动偷懒,导致返回的计算结果不正确。针对这些问题,云计算中的安全外包计算成为了近年来的重要研究话题之一,其目的在于利用云服务器的计算能力完成复杂的运算,同时保护运算所涉及的敏感输入和输出的隐私性,并有效验证云服务器返回结果的正确性。
矩阵求逆是一种常见的计算任务,在许多场景中有着广泛应用 [3] [4] [5] ,比如方程组求解、回归计算等。如果矩阵的维度为n × n,矩阵求逆的时间复杂度高达O(n2.373) [6] [7] 。当n很大时,矩阵求逆耗时很多,配置较弱的客户端往往难以快速完成这一技术,甚至无法承受其计算过程。通过按需租用云服务器,配置较弱的客户端能够以较低的代价完成矩阵求逆。然而,待求逆的矩阵往往是用户的隐私数据,并不能直接向云服务器暴露。为了应对这一矛盾,论文 [8] 提出了矩阵求逆安全外包问题,并设计了一种高效的实现机制,可以将用户端的计算量降低到O(n2)。然而,论文 [8] 的方案仅使用乘以随机数的方式对矩阵中的每个元素进行变换,这种方法会导致两方面的问题;1) 如果矩阵中某个元素等于0,这种变换方法会直接泄漏该元素的值,不能提供任何安全保护;2) 这种变换方法会泄漏多个元素乘积的比值,在攻击者获得部分元素值的情况下,会导致其他元素的泄漏。
针对上述问题,本文设计了一种新的矩阵求逆安全外包方案。新方案利用稠密矩阵对原始矩阵进行变换,使得变换过程既包括随机乘法又包括随机的加法,消除上述安全问题。重要的是,虽然使用稠密矩阵对原始矩阵进行变换,我们所提方案的依然可以将用户端的时间复杂度降到O(n2),能够有效提升计算效率。此外,我们还改进了结果验证机制,使用双验证策略,降低了错误结果被接受的概率。
论文其余部分安排如下。第2部分介绍了系统模型和设计目标;第3部分展示了我们的新方案;第4部分对新方案进行了分析和评估;第5部分总结了本文。
2. 系统型和设计目标
2.1. 系统模型
本文的系统模型结构如图1所示,其中包含两个参与者,分别是云服务器和用户。云服务器具有较强的计算能力,可以根据用户的需求完成计算过程。用户拥有私有的n × n维矩阵X,他希望获得矩阵X的逆矩阵Y。然而,用户只能承受O(n2)的计算复杂度,无法承受普通矩阵求逆所需要的时间复杂度。同时,用户的矩阵X包含了隐私数据,用户也无法将该矩阵直接和云服务器共享。为此,用户生成密钥K,利用密钥K将矩阵X变换为矩阵X',然后将矩阵X'发送云服务器,使得云服务器无法从X'推导出X的有用信息。接着,云服务器计算矩阵X'的逆矩阵Y' (即图1中f(·)表示矩阵求逆),并将返回给用户。最后,用户验证Y'的正确性,并根据Y'计算出矩阵X的逆Y。
相应地,基于云计算的矩阵求逆安全外包机制共包含五个子算法,其功能简介如下。
• Gen(λ)→K:用户根据安全参数λ生成密钥K,用于后续的加密和解密过程。
• Enc(K, X)→X':用户利用密钥K将私有输入X加密成X'。
• Compute(X')→Y':云服务器计算矩阵X'的逆矩阵Y'。
• Verify(Y')→0/1:用户验证云服务器返回值Y'的正确与否,1表示正确,0表示不正确。
• Dec(K, Y')→Y:用户在验证Y'正确的情况下,利用K解密Y'得到矩阵X的逆矩阵Y。

Figure 1. The system model of secure outsourcing computation based on cloud
图1. 基于云计算的安全外包计算系统模型结构
2.2. 设计目标
下面,我们从安全性和效率等方面分别描述我们的设计目标。
1) 输入隐私性:安全外包方案需要保护用户的输入数据的隐私性,即矩阵X是用户的隐私数据,在方案执行前后都不能泄漏给云服务器或任何第三方。
2) 输出隐私性:用户的输出结果Y也是隐私的,其隐私性需要有效保护,云服务器不能获得Y的有用信息。
3) 效率:用户端总的计算开销应该远小于直接矩阵求逆所需要的开销,即安全外包可以降低用户的的计算开销。
4) 正确性:用户能够以较高的概率验证云服务器返回的结果正确与否。如果云服务器返回的Y'是错误的,用户能够以很高的概率检测出不正确的输出;如果云服务器返回的的Y'是正确的,Y'能够通过用户的验证。
3. 方案设计
3.1. 主要思路
本文中,我们设计了一种利用稠密的随机矩阵对用户的输入矩阵X进行变换的方法。下面,我们先介绍方案的整体思路。
为了保护矩阵X,我们将使用随机的稠密矩阵DL和DR对矩阵X进行变换,它们分别对X进行左乘和右乘,即变换后的矩阵
。当矩阵的维度都是n × n时,计算两个矩阵相乘的时间复杂度是O(n3),因此简单使用这种方法虽然可以保护X的隐私性,但是无法降低用户端的计算开销。这里,我们使用如下方式生成随机的稠密矩阵DL和DR。令
, ,这里L和R是随机的对角矩阵,P和U是n*1的随机矩阵,Q和V是1 × n的随机矩阵。假设L和R的对角线元素依次分别是
和
,
,
,
,
。那么,
,这里L和R是随机的对角矩阵,P和U是n*1的随机矩阵,Q和V是1 × n的随机矩阵。假设L和R的对角线元素依次分别是
和
,
,
,
,
。那么,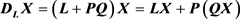 。不难看出,LX和P(QX)可以在O(n2)时间内完成,因此DLX的计算复杂度是O(n2)。类似地,我们可以在O(n2)时间内求出
。从安全性上看,DL和DR都是稠密矩阵,对矩阵X的变换过程同时包括随机的乘法和加法操作,因此可以避免文献 [8] 方案的安全问题。用户得到X'后,将其发送给云服务器。在云服务器返回矩阵X'的逆矩阵Y'给用户后,用户可以用如下方法解密Y',得到X的逆矩阵Y。
。不难看出,LX和P(QX)可以在O(n2)时间内完成,因此DLX的计算复杂度是O(n2)。类似地,我们可以在O(n2)时间内求出
。从安全性上看,DL和DR都是稠密矩阵,对矩阵X的变换过程同时包括随机的乘法和加法操作,因此可以避免文献 [8] 方案的安全问题。用户得到X'后,将其发送给云服务器。在云服务器返回矩阵X'的逆矩阵Y'给用户后,用户可以用如下方法解密Y',得到X的逆矩阵Y。
易于说明,用户可以在O(n2)时间内完成
计算。此外,当且仅当矩阵DL和DR都是可逆矩阵,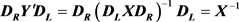 成立。下面,我们将介绍矩阵DL和DR中每个元素的生成方法,这个方法可以确保DL和DR都是可逆矩阵。
成立。下面,我们将介绍矩阵DL和DR中每个元素的生成方法,这个方法可以确保DL和DR都是可逆矩阵。
为此,我们先介绍以下引理。
引理1 ( [7] ):假设矩阵M是一个方阵,那么将M的任何一列乘以一个倍数然后加到另外一列,不会改变M的行列式。
引理2 ( [9] ):假设矩阵E,F,G,H的维度分别是a × a,a × b,b × a,b × b,且矩阵H是可逆的,那么
基于引理1和2,我们可以得到如下定理1。
定理1:假设
, ,其中L和R是随机的对角矩阵,P和U是n × 1的随机矩阵,Q和V是1 × n的随机矩阵。L和R的对角线元素依次分别是
和
,
,
,其中L和R是随机的对角矩阵,P和U是n × 1的随机矩阵,Q和V是1 × n的随机矩阵。L和R的对角线元素依次分别是
和
,
, 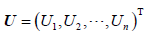 ,
,
。如果
,那么
,
,
。如果
,那么
即
,
。
证明:由于矩阵DL和DR的情况类似,下面我们先证明矩阵DL的行列式满足定理1。根据定理1的说明,我们可以看出
基于引理1,如果我们将矩阵DL的第一列乘以−Qi,然后加到第i列 ,不会改变矩阵DL的行列式。即在矩阵DL的第i列加上
后,可以得到
,不会改变矩阵DL的行列式。即在矩阵DL的第i列加上
后,可以得到
令矩阵
,
,
,H为一个
的对角矩阵,且H的对角元素依次为
。基于引理2,我们可以得到
此外,
,
。因此,
相似地,可以证明
。
综上所述,定理1是正确的。
根据定理1,通过如下方式我们可以确保矩阵DL和DR都是可逆的。
1) 对于i = 1到n,随机选择非零的Li和Ri。
2) 设定
,并对于i = 2到n,随机选择非零的{Pi, Qi}和{Ui, Vi};然后随机选择P1和U1,使得 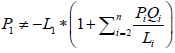 且
。
且
。
易于看出,上述方法可以确保
且
,从而可以确保矩阵DL和DR都是可逆的。
3.2. 方案步骤
基于上述思路,我们所提方案的具体步骤如下。
• Gen:用户1) 随机生成n × n对角矩阵L和R,其对角线元素依次分别是
和
,并且满足任意的Li和Ri都不等于0。2) 对于I = 2到n,分别随机选择非零的{Pi, Qi}和{Ui, Vi};然后随机选择P1和U1,使得
且
。3) 设定矩阵
,
,
,
。4) 将密钥K设置为
。
• Enc:用户利用密钥K将私有输入X加密成X',使得
。
• Compute:用户将加密后的矩阵X'发送给云服务器。云服务器计算矩阵X'的逆矩阵Y',并将矩阵Y'返回给用户。
• Verify:用户随机生成n × 1的矩阵
,然后计算
。用户比较S'和S,如果 S'=S,则返回值Y'通过验证;否则Y'没通过验证。
• Dec:在验证Y'正确的情况下,用户利用密钥K解密云服务器返回的矩阵Y',得到矩阵
。
4. 方案分析
下面,我们将分析本文所提方案的安全性、隐私性和运行效率,并利用模拟实验进行了评估。
4.1. 理论分析
正确性:我们通过以下两个定理说明本文所提方案的正确性。
定理2:本文所提方案中
和
都是可逆的。
证明:基于定理1,易于看出
因为
,
,
且
,所以确保
且
。即
和
都是可逆的。
定理3:通过本文所提方案,用户可以获得正确的矩阵Y,即矩阵Y是矩阵X的逆矩阵。
证明:在该方案中,我们有 且
。此外,定理2已经证明
和
都是可逆的。
且
。此外,定理2已经证明
和
都是可逆的。
因此,
,即矩阵Y是矩阵X的逆矩阵。
安全性:在我们的方案中,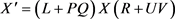 。服务器只能得到X',对
和
中的数据都是未知的。此外,
和
都是可逆的稠密矩阵,而且它们是用户随机选择的,因此服务器无法从矩阵X'推导出矩阵X的有用信息。考虑X中某个元素为0的特殊情况,在X'中该元素变成了其他元素的随机线性组合,因此云服务器也无法判断矩阵X中该值是否为0。所以,我们的方案可以实现用户输入的隐私性。
。服务器只能得到X',对
和
中的数据都是未知的。此外,
和
都是可逆的稠密矩阵,而且它们是用户随机选择的,因此服务器无法从矩阵X'推导出矩阵X的有用信息。考虑X中某个元素为0的特殊情况,在X'中该元素变成了其他元素的随机线性组合,因此云服务器也无法判断矩阵X中该值是否为0。所以,我们的方案可以实现用户输入的隐私性。
相应地,我们有
,即
。类似地,由于
和
对云服务器是随机的和未知的,所以服务器无法从矩阵Y'推导出矩阵Y的有用信息,即本文方案可以保护用户输出的隐私性。
计算复杂度:在我们的方案中,用户需要生成随机的
,并计算
和
。其中,生成随机K的时间复杂度是O(n),计算X'和Y的时间复杂度都是O(n2)。因此,用户的时间复杂度合计是O(n2)。云服务器端只需要完成矩阵求逆,计算矩阵X'的逆矩阵Y',因此云服务器的时间复杂度是O(n2.373)。
可以看出,该方案可以有效降低用户端的计算复杂度;同时云服务器只需要执行常规的的矩阵求逆运算,无需承担额外的计算。
4.2. 实验评估
我们进一步通过模拟实验验证了本文所提方案的运行效率。实验平台是配置有Intel Core(TM) i7-4770 3.4 GHz CPU和8.0 GB内存的计算机,模拟实验运行在Matlab R2013b上。
表1展示了模拟实验的运行结果。如表1所示,本方案可以有效降低用户端的计算时间。随着矩阵维度n的增长,用户运行时间降低的幅度逐渐增加。这是因为外包前用户执行矩阵求逆的时间复杂度是O(n2.373),通过本方案借助云服务器后用户的时间复杂度降低到O(n2),因此用户时间降低的比例会随着n的增加而变大。我们计算了用户直接进行矩阵求逆时间To和本方案中用户执行时间Tu的比值,记为用户加速比。从表1可以看出,在n取值为100到5000时,本方案中的用户加速比的为52.373到3858.564之间。维度n越大,用户加速比越大。这也与上述理论分析结果基本相符。
总的来说,本方案的方案可以利用云服务器有效提升用户的计算效率,减少用户的计算开销。

Table 1. Running time of simulation experiments
表1. 模拟实验运行时间
5. 结束语
本文提出了一种新的基于云计算的矩阵求逆安全外包方案。该方案实现了一种新的稠密随机矩阵生成方法及其快速的矩阵乘法,进而提出了利用稠密矩阵对用户矩阵进行安全的变换的方法,可以在支持矩阵求逆外包的同时有效提升用户输入输出的安全性。我们通过理论分析证明了所提方案的安全性和计算复杂度。最后,通过模拟实验,我们证实了所提方案可以有效减少用户的计算开销,提升其运算效率。
基金项目
本文工作受到国家重点研发计划(项目号:2017YFB0802300)的资助。
参考文献