1. 引言
晶界作为多晶材料微观组织的缺陷,由于原子的错排而具有比晶粒更高的能量。通常,人们将单位面积晶界所具有的附加自由能称为晶界能 [1] 。晶界能作为晶界的重要特性之一,影响着再结晶、晶粒长大以及其它与晶界相关的组织演变,并对材料的力学、物理和化学性能产生重要影响 [1] [2] 。1949年,Read和Shockley [3] 基于晶界的位错构成这一特点,推导出晶界能与取向差角的关系式,即著名的Read-Shockley公式,从而第一次以理论的形式诠释了晶界能的各向异性。然而,该公式未考虑位错间的相互作用,因而只适用于由离散位错组成的小角度晶界。近年来,随着原子模拟理论的发展,越来越多的人开始借助分子动力学在完整考虑晶界的晶体学取向和材料特性等的前提下计算晶界能 [4] [5] [6] 。
完整描述晶界的几何特征需要5个自由度,其中3个表示相邻晶粒间的取向差(常用角轴对形式表示),另2个表示晶界面的取向 [7] 。根据取向差角的大小,可将晶界分为小角度晶界和大角度晶界;根据晶界面与取向差轴间的几何关系,可将晶界分为倾斜晶界、扭转晶界、以及混合晶界;根据相邻两晶粒点阵在晶界是否有阵点重合,又可将晶界分为重位点阵(Coincidence-site lattice, CSL)晶界和非重位点阵(non-CSL)晶界 [7] 。已有研究表明,小角度晶界一般比大角度晶界具有更低的能量 [4] ,具有低指数或高面原子密度晶界面的晶界具有相对较低的能量 [8] ,晶界能与晶界膨胀体积间存在近似正线性相关性 [6] 等。关于晶界能的已有认识还包括,当相邻两点阵在晶界附近的重合程度越高时(即晶界对应的重位因子Σ越低时),晶界的结构畸变程度应该更低,从而晶界具有更低的能量 [9] [10] 。然而,Olmsted等 [4] 所计算的388组CSL晶界的能量表明,晶界能与Σ间无可见相关性。此外,对于不存在周期性结构和重位阵点的non-CSL晶界,长期以来研究者们 [9] [11] 都认为它们应该具有比CSL晶界更高的能量。然而,绝大多数实验和模拟研究(如文献 [4] [6] [12] [13] )所得晶界能都是针对CSL晶界,只有极少数研究 [5] [14] 获取了少量non-CSL晶界的能量。这些研究尚不能提供系统对比CSL和non-CSL晶界能量所需的数据。因此,有关晶界能与晶界两侧点阵重合度的相关性还有待进一步研究。
本研究将采用分子动力学模拟计算纯铝内多组CSL <111>晶界的能量以及在取向空间内与这些晶界接近的non-CSL晶界的能量,基于这些结果,定量分析晶界能与重位因子的相关性以及对比分析CSL和non-CSL晶界的能量,从而探究晶界两侧晶粒点阵的重合度对晶界能的影响。
2. 模拟方法与参数
2.1. 模拟方法
现主要有块状双晶 [6] 和球状双晶 [5] 两种分子动力学模型计算晶界能,这两种模型计算晶界能的原理相同,都是通过获取单位晶界面积上包含晶界的双晶体系总自由能与同等大小单晶体系总自由能差。前者由于采用周期性边界条件,晶界面内两个尺寸方向必须采用周期性边界条件,且相邻两晶粒沿该两方向的点阵周期长度必须存在最小公倍数,因而只适用于重位因子较小的CSL晶界 [6] 。后者采用自由表面,在应用时不受晶界取向参数的限制,从而可计算任意晶界的能量 [5] 。因此,本研究将采用球状模型计算各组晶界的能量。图1给出了球状双晶模型计算任意晶界能量的主要步骤。如图所示,具有取向
的球状单晶按一定要求转动后,分别获得取向为
和
的两个晶粒A和B。沿给定方向n将两个晶粒分别分割成两个同等大小的半球,随后将晶粒A和B的两个半球刚性对接成晶粒取向满足取向差
、晶界面法向平行于n的双晶。所构建球状单晶和双晶体系还需基于共轭梯度法进行能量最小化驰豫。驰豫后的单双晶体系被认为具有相同的自由表面能,因而单晶总自由能(
)与双晶总自由能(
)间的差异仅源自于双晶中存在的晶界,也即晶界能量
可基于下式获取:
(1)
其中S为球状双晶体系中晶界的面积,
,R为双晶半径。
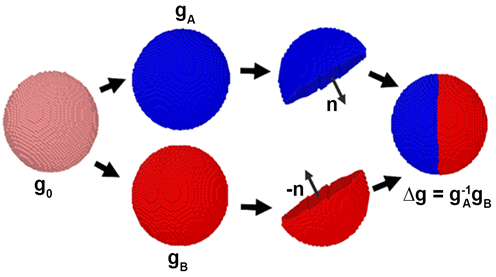
Figure 1. Illustration for constructing a spherical cell containing a grain boundary (GB) with misorientation
and boundary plane normal n.
图1. 基于球状双晶模型构建取向差为
和晶界面取向为n的晶界示意图
国内研究者张明亮 [15] 发现,球状模型必须引入块状模型中的原子删除操作 [6] ,否则所得晶界能会显著高于晶界能的理论值。引入该操作的主要目的是:删除球状模型中晶界附近可能存在的相距过近和能量过高的原子,构建给定晶界取向参数下的不同初始晶界结构,以获取状态更为稳定的晶界结构。该操作具体为:包含任意晶界的双晶体系在结构驰豫前,晶界处间距小于临界间距
的两相邻原子中任意一个原子将被删除;同时,为构建不同初始晶界结构,
以一定增量
在最小间距
和最大间距
间取值,最终选定所有初始晶界结构中对应能量最低者为晶界的结构。本研究在利用球状模型计算晶界能时,也引入原子删除操作以获取更为准确的晶界能。
2.2. 模拟参数
为探究晶界能与相邻晶粒点阵重合程度的相关性,本研究将以被大量研究的纯铝<110>对称倾斜晶界(STGB)和<110>扭转晶界(TWGB)两组晶界为例,选取每组晶界下一定数量的CSL和non-CSL晶界,并基于球状模型计算晶界能。鉴于纯铝具有面心立方晶体对称性,也即<110>轴为二次旋转对称轴,因而将在0~180˚取向差角(θ)范围内选取各类晶界。同时,为分析不同晶界类型下晶界能与点阵重合度的相关性,将选取具有相同取向差角的<110> STGB和TWGB,因而两组晶界下对应各个CSL和non-CSL晶界的选取方法相同。其中,CSL <110>晶界对应θ的选取方法是:首先获取<110>轴下Ʃ < 3000的所有CSL晶界对应的取向差角
,再从
集合中筛选出不小于且又最接近于
的角集合
,
就是最终所选定的取向差角。non-CSL <110>晶界对应θ的选取方法是:以5˚等间隔在0~180˚内均匀地选取一系列θ。表1给出了基于以上方法所选取的各晶界。
在利用球状模型计算表1中各晶界的能量前,还需利用文献 [6] 中的晶体学理论基于各晶界对应的取向差轴和取向差角推导构建双晶模型所需两个晶粒的取向。本研究所采用球状模型的半径为5 nm,原子删除参数为
,
和ds = 0.05 Å。其中,
表示纯铝内的最小原子间距,a0为点阵常数4.05 Å。选用文献 [16] 提出的2NN-MEAM纯铝原子势函数来描述原子的能量和相互作用力。本研究所有分子动力学模拟都是利用Lammps [17] 软件。
3. 结果与讨论
为分析晶界两侧点阵的重合度对晶界能的影响,图2以<110> STGB和<110> TWGB为例,给出了对应CSL和non-CSL晶界的能量随取向差角的变化。由图2(a)可知,从整体来看,两类晶界的能量随取向差角的变化趋势保持了一致,都在θ = 70˚和130˚附近存在两个明显的能量低谷,在θ = 40˚和105˚附近存在两个相对较小的能量低谷。当前研究所得<110> STGB能量随取向差角的变化趋势与已有实验研究 [12] [14] 所测趋势相同,即当前所计算的晶界能结果是准确可靠的。与此同时,从图2(a)还可观察到,当CSL和non-CSL晶界对应的取向差角相近时,两类晶界的能量也随之相近甚至一致。以上观察表明,对于<110> STGB,无论两相邻晶粒的点阵是否在晶界附近存在重合,晶界能随取向差的变化趋势保持不变;晶界能的绝对大小不受点阵是否重合的影响,但会因取向差角改变而发生明显变化。对比图2(a)和图2(b)可知,<110> STGB和<110> TWGB能量的相对大小以及随取向差角的变化趋势均明显不同,<110> STGB的平均能量要低于<110> TWGB。对于<110> TWGB,CSL和non-CSL晶界的能量随取向差角的变化趋相同,当取向差角相近时两类晶界的能量也随之相近。该特征与<110> STGB呈现的能量特征相同。这表明,晶界能与相邻晶粒点阵是否重合并不相关的特征不受晶界类型的影响。综合以上结果和分析可得出,早期研究 [9] [11] 认为non-CSL晶界具有比CSL晶界更高能量的观点并不正确,晶界能的相对大小与晶界两侧点阵是否存在重合无关。
为进一步定量分析晶界能与晶界两侧点阵重合度高低的相关性,图3分别给出了<110> STGB和<110> TWGB能量随各晶界对应Ʃ的变化。由图可知,对于STGB和TWGB,虽然重位因子相同时两组晶界的能量存在明显差异,但两组晶界的能量与对应重位因子整体上都不会呈现任何可见相关性。从整体来看,对于具有相同Ʃ的晶界,其能量会在较大范围内波动。长期以来认为低Ʃ晶界具有相对较低能量的观点(如文献 [9] [10] )显然是不正确的。例如,对于具有最小Ʃ的Ʃ3晶界,其能量并不比其它高Ʃ晶界的能量低,

Table 1. CSL and non-CSL <110> GBs sampled in this study
表1. 本研究所选取的CSL和non-CSL <110>晶界
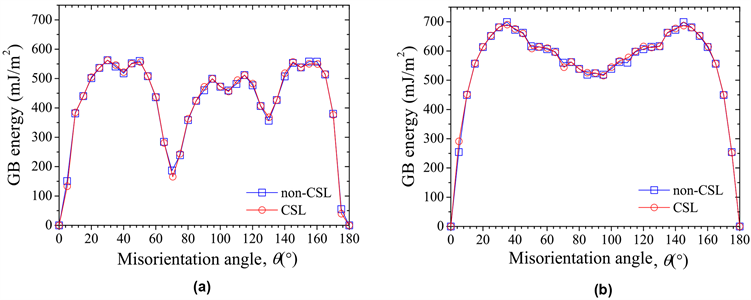
Figure 2. Comparison of energies for CSL and non-CSL GBs calculated using the sphere model: (a) <110> STGB; (b) <110> TWGB
图2. 球状模型计算所得CSL和non-CSL晶界能量的对比:(a) <110> STGB;(b) <110> TWGB
在两组晶界下的能量波动范围可达到400 mJ/m2。以上观察与Olmsted等 [4] 统计性分析金属铝内晶界能与Ʃ相关性的结果一致,尽管当前研究所考虑的最大Ʃ高达2993,而后者只有385。

Figure 3. GB energies plotted against Ʃ for <110> STGB and <110> TWGB
图3. <110> STGB和<110> TWGB能量随Ʃ变化
本研究将晶界能分析扩展到高Ʃ晶界和非CSL晶界时发现,这两种晶界往往可能具有极低的能量(见图2中晶界能曲线上的能量低谷)。进一步分析发现,这些晶界实质上是符合Read-Shockley公式所描述的“小角度晶界”,也即晶界结构可基于位错模型表征的晶界。综合以上分析可知,晶界能的相对高低与晶界对应重位因子的高低无可见相关性,也即不能基于重位因子来预测晶界能量的高低。其本质原因是,晶界能受到晶界5个取向参数的共同影响,且晶界能与这5个参数呈现十分复杂的相关性 [4] [18] ;重位因子是与相邻晶粒间取向差(取向差可体现晶界5个取向参数中的3个参数)部分相关的参数,各晶界对应的取向差相同或不同并不意味着重位因子也随之相同或不同。可见,重位因子只能非常有限地体现晶界取向的部分参数,因而无法用于预测晶界能。
4. 结论
本研究通过球状双晶分子动力学模型计算了纯铝<110> STGB和<110> TWGB的能量,两组晶界下均考虑了重位因子高达2993的CSL晶界以及很少被研究的non-CSL晶界,基于计算所得晶界能探讨分析了晶界能与晶界两侧相邻点阵重合度的相关性。分析后发现:1) CSL和non-CSL晶界的能量与晶界对应取向差角的变化趋势相同,且当取向差接近时两类晶界的能量也十分接近,即晶界能的相对高低与相邻晶粒点阵是否存在重合无关;2) 对于具有显著不同重位因子的晶界,它们的能量随重位因子变化时并不呈现任何可见规律或趋势,也即晶界能的相对高低与晶界两侧相邻点阵重合度的高低无可见相关性。这些发现揭示了晶界能与点阵重合度的相关性,且有助于进一步了解晶界能与晶界5个取向参数的关联以及晶界能的各向异性。