Runge现象的研究

Research on Runge Phenomenon

摘要: 首先，本文解释了高次多项式插值时产生的Runge现象，并通过计算系统误差证明了插值多项式发散，从而导致了该现象。其次，以Runge函数、反三角函数和分式函数为例，运用等间距牛顿插值求出函数的插值多项式，进而求出其插值余项函数表达式，然后计算每相邻两个节点的中点处的误差，判断上述三个函数产生了Runge现象。第三，介绍并验证了采用切比雪夫节点、分段线性插值和三次样条插值三个常用的算法，能够避免上述函数产生Runge现象。最后，创新性地提出逼近性能指标，并基于最优多项式构造系数与阶次双确定法，该算法在避免Runge现象的同时具有优异的函数逼近效果，且运行速度有极大提升。

Abstract: Firstly, this paper explains the Runge phenomenon generated by high-order polynomial inter- polation, and proves that the interpolation polynomial divergence is obtained by calculating the systematic error. Secondly, taking the Runge function, inverse trigonometric function and fractional function as examples, the interpolation polynomial of the function is obtained by using the equally spaced Newton interpolation, and then the interpolation residual function expression is obtained, and then the midpoint of adjacent two nodes is calculated. The error at the location determines that the above three functions have generated the Runge phenomenon. Thirdly, the three algorithms of Chebyshev node, piecewise linear interpolation and cubic spline interpolation are introduced and verified, which can avoid the Runge phenomenon. Finally, the approximation performance index is proposed, and based on the optimal polynomial construction coefficient and order double determination method, the algorithm has excellent function approximation effect while avoiding the Runge phenomenon.

1. 引言

在数值方法领域中，常常需要理由插值法对函数进行逼近，多项式插值法是常用的方法之一，不过，对于某些函数而言，多项式插值法的逼近效果不佳，这是因为产生了Runge现象。Runge现象是指，对于Runge函数，在区间[-1,1]内，等距选取插值点并采用插值多项式进行逼近，逼近多项式在区间的两端会产生振荡现象，且插值多项式的阶次越高，振荡现象就越明显，从而造成极大的逼近误差。因此，通常认为，Runge函数不能使用等距节点的高次多项式插值进行函数逼近。为良好地逼近Runge函数，解决Runge现象，通常使用切比雪夫节点代替等距插值点(使逼近误差随插值多项式的阶次的增大而减少)、分段线性插值和低次样条插值代替多项式插值、放弃个别点以及系数与阶次双确定法，避免龙格现象 [1] 。

2. 分析Runge现象

20世纪初，数学家龙格指出，对于连续函数：

$R\left(x\right)=\frac{1}{1+25x^2}$

在区间[−1,1]内，不应采用基于等距节点的高次插值多项式对该函数进行逼近。在本文中，称式上式为Runge函数。为更好地解释Runge现象，在区间[−1,1]内取 $n+1$ 个等距插值节点

$\left\{\left(x_i,y_i\right)|x_i=-1+2i/n,y_i=R\left(x_i\right),i=0,1,\cdots ,n\right\}$

其中n为插值多项式的阶次。则可构造逼近Runge函数的插值多项式，记为：

$p_n\left(x\right)=a_n{x}^n+a_{n-1}{x}^{n-1}+\cdots +a_0$

其中 $a\ne 0$ 且满足 $p_n\left(x_i\right)=y_i$ 。为了确定其系数，从而确定式 $p_n\left(x\right)$，首先定义系数列向量a、插值输入幂激励矩阵V和插值输出列向量y分别为：

$\begin{array}{l}a={\left[a_0,a_1,\cdots ,a_n\right]}^{\text{T}}\in R^{n+1}\\ V=\left(\begin{array}{cccc}1& x_0& \cdots & x_0^n\\ 1& x_1& \cdots & x_1^n\\ ⋮& ⋮& & ⋮\\ 1& x_n& \cdots & x_n^n\end{array}\right)\in R^{\left(n+1\right)\times \left(n+1\right)}\\ y={\left[y_0,y_1,\cdots ,y_n\right]}^{\text{T}}\in R^{n+1}\end{array}$

根据以上定义，由式可得方程 $Va=y$ 。由于矩阵V的行列式不为零，即矩阵V可逆，该方程有惟一解 [2] ：

$a=V^{-1}y$

其中上标−1表示的是矩阵的逆。通过公式 $a=V^{-1}y$ 可确定系数列向量a，即式 $p_n\left(x\right)$，进而构造出Runge函数的逼近插值多项式。但是，当矩阵V的维数偏大时，求矩阵的逆将产生巨大的计算量。所以，为简化计算，可通过Lagrange插值法构建插值多项式。设Lagrange插值的多项式为：

$p_n\left(x\right)={\displaystyle {\sum }_{k=0}^0{y}_k{L}_{n,k}(x)}$

其中：

$L_{n,k}\left(x\right)=\frac{{\displaystyle \underset{\begin{array}{l}i=0\\ i\ne k\end{array}}{\overset{n}{\prod }}\left(x-x_i\right)}}{{\displaystyle \underset{\begin{array}{l}i=0\\ i\ne k\end{array}}{\overset{n}{\prod }}\left(x_k-x_i\right)}}$

实际上，Lagrange插值法所构建的多项式和通过公式 $a=V^{-1}y$ 确定的多项式是相同的。不过这两种构建的插值多项式在区间[−1,1]内都不能很好的逼近Runge函数。当阶次为n的Lagrange插值多项式逼近Runge函数时，其效果如图所示。从图中可知，在区间两侧插值多项式曲线产生振荡十分明显，且这种振荡随插值多项式阶次增加而变得严重，这种现象被称为Runge现象。具体如图1~3所示 [3] 。

$R\left(x\right)=\frac{1}{1+25x^2}$

Figure 1. Runge function equidistant node langrage interpolation

图1. Runge函数等距节点Langrage插值

$f\left(x\right)=\arctan (x)$

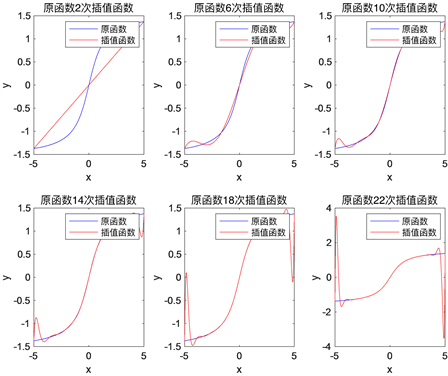
Figure 2. Anti-triangular function equidistant node Langrage interpolation

图2. 反三角函数等距节点Langrage插值

$g\left(x\right)=\frac{x}{1+x^4}$

Figure 3. Fractional function equidistant node Langrage interpolation

图3. 分式函数等距节点Langrage插值

3. Runge现象产生的原因

Runge现象是由系统误差造成的。一般的插值余项公式为：

$R_n\left(x\right)=f\left(x\right)-p_n\left(x\right)=\frac{1}{\left(n+1\right)!}{\displaystyle \underset{j=0}{\overset{n}{\prod }}\left(x-x_j^{\left(n\right)}\right)}{f}^{\left(n+1\right)}(\xi )$

其中 ${\left\{x_j^{\left(n\right)}\right\}}_{j=0}^n$ 为插值区间 $\left[a,b\right]$ 中的插值节点， $\xi$ 为 $\left[a,b\right]$ 区间中一点。Runge现象说的是，对 $f\left(x\right)=\frac{1}{1+x^2}$ 在区间 $\left[-5,5\right]$ 上进行n次多项式插值，当 $n\to \infty$ 时， $p_n\left(x\right)$ 不趋近于 $f\left(x\right)$ 。更确切的说，当 $\left|x\right|<x_c\approx 3.63$ 时， $p_n\left(x\right)\to f\left(x\right)$， $\max \left|R_n\left(x\right)\right|\to 0$，当 $x_c<\left|x\right|<5$ 时， $p_n\left(x\right)$ 不趋近于 $f\left(x\right)$， $\max \left|R_n\left(x\right)\right|$ 不趋近于0。

解释这一现象，直接计算

$\left|R_n\left(x\right)\right|\le \frac{1}{\left(n+1\right)!}\max \left\{\underset{j=1}{\overset{n}{{\displaystyle \prod }}}\left(x-x_j^{\left(n\right)}\right)\right\}\max \left\{f^{\left(n+1\right)}\left(x\right)\right\}$

很困难，因为微分项 $\max \left\{f^{\left(n+1\right)}\left(x\right)\right\}$ 不太容易直求导计算。为方便起见，令

$w_n\left(x\right)=\underset{j=0}{\overset{n}{{\displaystyle \prod }}}\left(x-x_j^{(n)}\right)$

复变函数中的Cauchy积分公式 $f^{\left(n\right)}\left(\xi \right)=\frac{n!}{2\text{π}i}\underset{C}{{\displaystyle \int }}\frac{f\left(z\right)}{{\left(z-\xi \right)}^{n+1}}\text{d}z$ 可以很方便的计算 $f^{\left(n\right)}\left(\xi \right)$ 的值，故将插

值余项公式延拓到复平面上，并应用Cauchy积分公式，得

$R_n\left(z\right)=\frac{1}{\left(n+1\right)!}{w}_n\left(z\right)\frac{\left(n+1\right)!}{2\text{π}i}\underset{C_T}{{\displaystyle \int }}\frac{f\left(\xi \right)}{w_n\left(\xi \right)\left(\xi -z\right)}\text{d}\xi$

其中 $C_T$ 是区域T的边界，区域T应满足f在T中解析且所有插值节点都在T中。(注意， $f\left(x\right)=\frac{1}{1+x^2}$ 的奇点为 $\pm i$ 故区域不能包含 $\pm i$ 。)

化简，得到

$f^{\left(n\right)}\left(\xi \right)=\frac{1}{2\text{π}i}\underset{C}{{\displaystyle \int }}\frac{w_n\left(z\right)}{w_n\left(\xi \right)}\frac{f\left(\xi \right)}{\xi -z}\text{d}\xi$

所以现在的关键就是通过分析函数 $w_n\left(z\right)$ 在 $n\to \infty$ 时的性态，选择一个围道，来估计积分的值。

$w_n\left(z\right)=r^n$ 的图像如图4。

Figure 4. Function image

图4. $w_n\left(z\right)=r^n$ 函数图像

这是当 $n=3$ 时，三个节点分别取 $0,1,2i$ 时的图象。随着r的增大，图象逐渐外扩。当r足够大时， $w_n\left(z\right)=r^n$ 的图象很接近一个包含所有节点的圆。因此我们可以选取 $w_n\left(\xi \right)=r^n$ 作为积分的围道 $C_1$ 。此时对 $C_1$ 内部任意的z， $\underset{n\to \infty }{\lim }\left|\frac{w_n\left(z\right)}{w_n\left(\xi \right)}\right|=0$ ( $w_n\left(z\right)=r_1^n$ 且 $r_1<r$ )，而对于 $C_1$ 外部任意的z， $\underset{n\to \infty }{\lim }\left|\frac{w_n\left(z\right)}{w_n\left(\xi \right)}\right|=\infty$ ( $w_n\left(z\right)=r_2$ 且 $r_2>r$ )。于是，当 $C_1$ 不包含 $f\left(z\right)$ 的奇点 $\pm i$ 时，可以直接选取 $C_1$ 做围道计算 $R_n\left(z\right)$，此时

$\underset{n\to \infty }{\lim }{R}_n\left(z\right)=M\underset{n\to \infty }{\lim }\left|\frac{w_n\left(z\right)}{w_n\left(\xi \right)}\right|=0$

随着r变大，曲线 $C_1$ 与x轴正方向交点向右移动。当 $C_1$ 恰好经过 $\pm i$ 时，曲线 $C_1$ 与x轴正方向交点为 $x_c\approx 3.63$ 。也就是说，当 $\left|x\right|>x_c$ 时，可以选取 $C_1$ 使x在 $C_1$ 内部而 $\pm i$ 在 $C_1$ 外部，这时误差估计满足上式，插值多项式收敛。而当 $r>x_c$ 时，奇点 $\pm i$ 在 $C_1$ 的内部，因此需在奇点附近挖“洞”，记“洞”的边缘为 $C^{*}$，此时有

$\underset{n\to \infty }{\lim }{R}_n\left(z\right)=\underset{n\to \infty }{\lim }\frac{1}{z\text{π}i}\left({\displaystyle \underset{C_1}{\int }\frac{w_n\left(z\right)}{w_n\left(\xi \right)}\frac{f\left(\xi \right)}{\xi -z}}-{\displaystyle \underset{C^{*}}{\int }\frac{w_n\left(z\right)}{w_n\left(\xi \right)}\frac{f\left(\xi \right)}{\xi -z}}\right)=0-\infty =\infty$

此时插值多项式发散，因此由于系统误差产生了Runge现象。

4. 避免Runge现象的算法

4.1. 常用算法

$R\left(x\right)=\frac{1}{1+25x^2}$， $f\left(x\right)=\arctan \left(x\right)$， $g\left(x\right)=\frac{x}{1+x^4}$

下面将分别用三种不同的插值方法对以上三个函数进行插值，并分析是否产生Runge现象。

4.1.1. 采用切比雪夫节点

此处根据Lagrange插值的具体算法进行编程，但插值节点不再是等距分布，而是如下形式：

$x_i=\cos \left(\frac{2i+1}{42}\text{π}\right)\left(i=0,1,2,\cdots ,20\right)$

从图5~7 [3] 中看出，插值曲线与原曲线吻合的很好，没有产生明显的Runge现象。

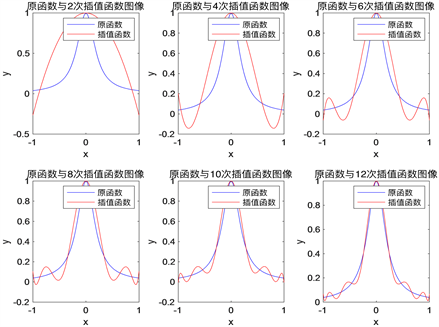
Figure 5. Runge function Chebyshev node Langrage interpolation

图5. Runge函数切比雪夫节点Langrage插值

Figure 6. Anti-triangular function Chebyshev node Langrage interpolation

图6. 反三角函数切比雪夫节点Langrage插值

Figure 7. Fractional function Chebyshev node Langrage interpolation

图7. 分式函数切比雪夫节点Langrage插值

由于切比雪夫插值点定义为

$x_k=\frac{b+a}{2}+\frac{b-a}{2}\cos \left(\frac{\left(2k-1\right)\text{π}}{2\left(n+1\right)}\right),k=1,2,\cdots ,n+1$

可以看出切比雪夫点恰好是以 $\left(0,\frac{b+a}{2}\right)$ 为圆心， $\frac{b-a}{2}$ 为半径的圆的上半部分圆周上等距分布的点，

而对应到横坐标就是切比雪夫零点，其表现是在接近区间的两端很密集。前面等距节点的高次插值中，在插值区两端出现龙格现象，两端误差较大，这就需要在两端用更多的点来插值才可以减小误差，而切比雪夫零点解决了这个问题，所以用切比雪夫零点插值可以很好的避免出现龙格现象，切比雪夫零点要比等距节点更好。

4.1.2. 采用分段线性插值

分段线性插值只需要将每个节点对应的函数值求出再将相邻的数据点两两用直线相连即可。此处采用了等距节点，从图中看出，此处分段线性插值的效果也还是不错的，二者只在区间中部略微存在一些偏差，而在其他区域整体上吻合的很好，并且不存在Runge现象，如图8~10所示。

Figure 8. Runge function isometric node piecewise linear interpolation

图8. Runge函数等距节点分段线性插值

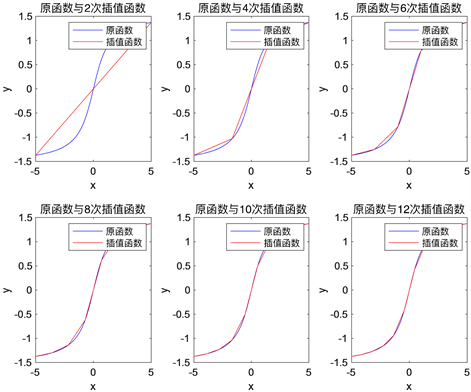
Figure 9. Inverse trigonometric function equidistant node piecewise linear interpolation

图9. 反三角函数函数等距节点分段线性插值

Figure 10. Fractional function equidistant node piecewise linear interpolation

图10. 分式函数等距节点分段线性插值

由于分段线性插值通过对插值区间分段的方法将插值函数的次数有效降低，因而即使是等距节点分布，也很好地避免了出现Runge现象的倾向。

4.1.3. 采用三次样条插值

三次样条插值此处依然采用等距节点，从图11~13 [3] 中看出，三次样条插值的效果优于分段线性插值，三次样条插值曲线和原曲线在整个插值区间都基本处于重合状态，几乎没有肉眼可见的偏差。同样，由于三次样条插值的插值函数最高次数只有3，在等距节点下也没有产生Runge现象。

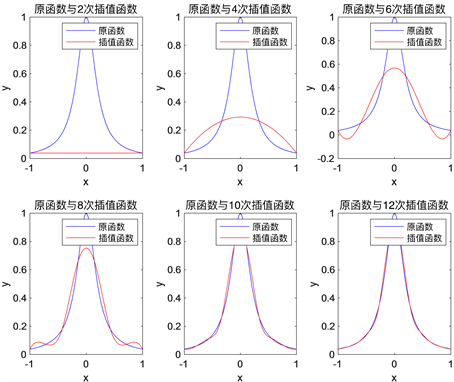
Figure 11. Runge function equidistant node cubic spline interpolation

图11. Runge函数等距节点三次样条插值

Figure 12. Anti-triangular function equidistant node cubic spline interpolation

图12. 反三角函数等距节点三次样条插值

Figure 13. Fractional function equidistant node cubic spline interpolation

图13. 分式函数等距节点三次样条插值

4.2. 结果分析

本文通过matlab和C语言编程分别Lagrange插值法、分段线性插值法、三次样条插值法以及系数阶次双确定法，对Runge函数、反三角函数和分式函数进行了插值逼近，并通过分析计算结果主要得到了以下结论：

1) 对于高次插值多项式，若适当选取插值节点能够在一定程度上抑制Runge现象。本文中，各函数采用切比雪夫节点Lagrange插值多项式，由于采用了中间疏两边密的非等距结点，而不是Newton插值多项式所用的等距节点，有效地抑制或消除了本应出现的Runge现象。

2) 降低插值多项式的次数能有效避免Runge现象。本实验中，分段线性插值法(各区间上均为1次)和三次样条插值法(最高次数为3)都取得了较为理想的差值逼近效果，没有出现Runge现象，且在整个插值区间都与原函数的图像吻合的很好。

5. 结论

综上，在实际运用中，为了取得较好的插值逼近效果，应尽量保证以下几点：不采用次数过高的插值多项式；适当选取插值节点；避免函数值突变，若不得已对存在不连续点的函数进行插值逼近，可以尝试分段插值，并将不连续点都处理到子区间的端点上，从而原函数在各子区间内分段连续，以便提高插值逼近的效果。