1. 引言
细胞自动机(Cellular Automata,简称CA)是一种时间、空间和状态均离散的数学模型,由John Von Neumann于1951年正式提出,用于模拟20世纪50年代生命系统中的自我复制现象 [1] 。1969年,G. A. Hedlund首先从数学角度把细胞自动机看作符号空间上的位移映射的自同态,刻画了一维细胞自动机的一些动力学行为,开创了细胞自动机数学理论研究的先河 [2] 。20世纪70年代,数学家J. H. Conway提出了一种能够进行普适计算的、结构简单的二维细胞自动机——“生命游戏(Game of life)”,使得细胞自动机的研究再度兴起 [3] 。20世纪80年代初,Stephen Wolfram引导了细胞自动机理论研究的新阶段 [4] 。他首先提出了一维的状态数为2且邻域半径为1的基本细胞自动机(Elementary Cellular Automata,简称ECA),并在大量计算机实验的基础上,通过观察待定规则产生的演化行为将基本细胞自动机分为:稳定、周期、混沌和复杂4类 [5] [6] [7] 。随后,Leon O. Chua等人利用非线性动力学的一套方法严格分析了Wolfram的经验主义观察结果 [8] [9] [10] [11] 。发展至今日,细胞自动机的理论已经十分成熟,而且有了很好的拓展。
本篇文章中,我们从拓扑动力系统的角度对细胞自动机的单射、满射、同胚性质进行研究。设X是符号空间,
是X上的位移映射,称映射
是细胞自动机,如果f连续且
,即是把细胞自动机看作是符号空间上的连续自映射。我们利用拓扑熵的一般性质证明了经典的Garden定理,即一维细胞自动机为同胚映射当且仅当它为单射 [12] [13] 。并且,利用该方法可以很方便地将Garden定理推广到高维情形,即任意维细胞自动机为同胚映射等价于它为单射。最后我们给出了基本细胞自动机中所有的同胚映射,以及几个是满射但不是同胚映射的细胞自动机的例子。
2. 预备知识
在本节中,我们将介绍细胞自动机,符号系统和拓扑熵的概念。首先说明一些动力系统中的记号:
我们用
表示拓扑动力系统,即X是一个紧致度量空间,
是连续映射;用
等表示X的开覆盖。记
,则
也是X的开覆盖。
2.1. 符号系统
2.1.1. 一维符号系统
设整数
,任取k个不同符号,例如取
,记
,称S为k个符号组成的
状态空间,其中每一个符号也称作状态。赋S以离散拓扑,则S为紧致拓扑空间 [14] 。
作拓扑积
,
这里的Z表示全体整数的集合,记号*表示x中第0个符号(坐标)所在的位置。
对
,定义
,
其中
容易证明,d是
上的度量,且它诱导的拓扑与乘积拓扑等价。文 [14] [15] [16] 中证明了
是
一个完备的,完全不连通的紧致空间。称
为一维k-符号序列空间,简称为一维符号空间。
在
上定义位移映射:
即在
的作用下,
中点的坐标依次向左移动一位,因此,也称
为左移映射。称
为S上的一维符号系统。
2.1.2. 二维符号系统
仍记
为
个符号组成的集合,记
。对于每一个
,用记号*表示第(0, 0)个符号(因子)所在的位置,即
在
中定义距离为
。
显然上述定义是合理的。文 [17] 证明了度量空间
是紧致的、完备的、完全不连通的Huasdorff
空间,并称
为二维k-符号序列空间,简称二维符号空间。
分别对两个坐标定义位移映射
为
,
。其中
表示
中
位置的元素
。称
为S上的二维符号系统。类似地,可以定义d维符号系统。
2.2. CA的定义
细胞自动机(Cellular Automata,简称CA)是一类时间、空间和状态均离散的数学模型。构成细胞自动机的四个基本要素分别是:细胞(cell)、网格(lattice)、邻域(neighborhood)和规则(rule) [18] 。最简单的情况下细胞可以取0和1两个状态;网格是指细胞活动的空间;邻域一般指某个细胞自身及其直接相邻的细胞,常见的邻域有Neumann邻域和Moore邻域 [7] ;规则则规定了细胞间的相互作用方式。
1969年,数学家G. A. Hedlund给出如下细胞自动机的定义 [2] :
定义2.1 设f是
上的连续映射,如果紧致系统
满足条件
,则称f是一个一
维细胞自动机,其中
表示定义在状态集S上的符号空间,
为左移映射。
类似于一维细胞自动机的定义方式,我们可以定义高维细胞自动机。
定义2.2 设f是
上的连续映射,如果紧致系统
满足条件
,则称f是一个d维细胞自动机,其中
表示定义在状态集S上的d维符号空间,
为第i个坐标上的位移映射,即
,
。其中
表示
中
位置的元素。
2.3. 拓扑熵的定义
动力系统中拓扑熵的定义有多种方法,这里我们用开覆盖来定义 [19] 。
设
是一个拓扑动力系统,
是X的一个开覆盖,用
表示
的子覆盖的基数的下确界,即
{
:
是
的子覆盖}。因为X是紧致的,所以
是一个正整数。定义开覆盖
的拓扑熵为
。
定义2.3 设
是一个拓扑动力系统,
是X的一个开覆盖,定义T关于
的拓扑熵为
,T的拓扑熵为
,其中
取遍X的开覆盖。
下面给出与拓扑熵相关的几个命题:
命题2.1 设
是两个拓扑动力系统且拓扑共轭(即存在同胚映射
,使得
),则
。也就是说拓扑熵是一个拓扑共轭不变量。
命题2.2 设
是一维符号系统,则
。
命题2.3 设
是一维符号系统。如果
是X的闭子集,且
,那么
限制在
上的拓扑熵为:
,
其中
表示使得集合
非空的n-元组
的个数。
类似于命题2.3中一维符号系统拓扑熵的定义方式,Berger在文 [20] 中给出了二维符号系统拓扑熵的如下定义:
定义2.4 设
是一个二维符号动力系统,Y是X的子系统,定义
的拓扑熵为
,
其中
表示使得集合
非空的
-元组
的个数。
根据Berger的定义,显然有
,因此
。
命题2.4 设
和
是两个二维符号系统且拓扑共轭,即存在X到Y的同胚映射
,使得
,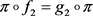 。那么,
[20] 。也就是说,Berger定义的拓扑熵也是一个共轭不变量。
。那么,
[20] 。也就是说,Berger定义的拓扑熵也是一个共轭不变量。
3. 单射的CA必定是同胚映射
本节我们利用拓扑熵的性质这一方法给出Garden定理的证明,并利用该方法将Garden定理推广到任意维CA的情形。
定理3.1 设
,其中
是一个整数。再设
是一个CA,则f是同胚映
射当且仅当f是单射。
为了证明此定理,我们首先给出一个引理:
引理3.1 设
,其中
是一个整数。再设
是一个单射的CA,则f是
满射。
证明:我们首先说明一维的情形:
事实上,当
时,上述结论由Garden-of-Eden定理即可直接得到 [12] [13] 。在这里,我们用拓扑熵的方法进行证明。
假设f不是满的,则
是一个非空开集,从而存在柱集
。由细胞自动机定义,
,所以
是
-不变的。因此,
是具有禁止词“
”的有限型位移系统
的子系统,即Y中的每个点(双边符号序列)均不含有词“
”。下面我们证明
。
由定理2.3,
从而,
。另一方面,考虑映射
,由于
,且f是X到
的单射、满射,所以
与
在映射f下拓扑共轭。于是,
,矛盾。故f是满射。
下面我们说明高维的情形,为了表述方便,我们只对二维的情形给出证明。
类似于
的证明,我们假设f不是满的。那么
是一个非空开集,于是,存在柱集
,其中
是一个m × m方块。因为
,所以
是
-不变的
。因此,
是具有禁止词
的有限型位移系统
的子系统,即
Y中的每个点均不含有词
。从而,
另一方面,映射
是一个共轭映射,于是,
,矛盾,故f是满射。
下面我们给出定理3.1的证明:
证明:充分性是显然的,下面证明必要性:
由一般的拓扑理论,一个从紧致空间到度量空间的连续映射是同胚的,当且仅当它既是单射又是满射 [21] 。由于X是一个紧致度量空间,我们直接通过上述引理即可得到结论。
4. 一些例子
例1 基本细胞自动机(Elementary Cellular Automata,简称ECA)是指状态数为2、邻域半径为1的一维细胞自动机 [4] 。256个基本细胞自动机
中的同胚映射有:
,
,
,
,
,
,其中
是恒等映射,
是镜像映射,
和
分别是左移映射和右移映射,
,
且
和
是拓扑共轭的。即对
,有
,
,
,
,
,
。
证明:显然
,
,
,
都是单射,所以
和
也是单射。于是,由定理3.1知,
,
,
,
,
,
都是同胚映射。下面证明
和
是拓扑共轭的,为此,需构造同胚映射
使得
。
在
上定义映射
为:
即在
的作用下,
中点的坐标关于坐标零做了翻转。显然
是
上的同胚映射。
对
,
。
因此,
。由x的任意性得
。
例2 满射的CA不一定是同胚,例如ECA中的规则102 (即
)是满射,但不是单射,因而不是同胚映射。
证明:由于
,
在布尔函数真值表中
,
令
,有
,
。
于是,
,其中
表示逻辑语言“异或”,即
,
。显然
是满射,下面说明
不是单射。
取
,则有
。
因此,
不是单射。从而,
不是同胚。
下面的例子说明存在
上的连续自映射f满足:f是单射,但不是同胚。因此,上述的结论要求
所讨论的映射是CA。
例3 设
,定义映射
为
,
,
。也就是说,通过在x的每两个符号之间插入0来构造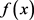 。容易看出f是连续的,但是,对于任意的
,
。容易看出f是连续的,但是,对于任意的
,
,
。
所以
,因此f不是CA。进一步,f是单射,但是由于每一个
都不包含长度为2的词“11”,因此f不是满射。
基金项目
国家自然科学基金(编号:11401220)资助。