1. 引言
目前,无线随钻测量数据传输时,地面接收的泥浆脉冲信号常常存在基线漂移现象。随钻泥浆脉冲信号解码中,消除信号的基线漂移是重要的预处理工作,直接关系到后期解码的正确率,是泥浆脉冲信号解码技术的关键环节 [1] [2] [3] 。形态学滤波消除信号基线漂移的研究多见于医学中的心电信号去噪,其效果好、适应性强、计算量较小 [4] [5] [6] [7] 。医学心电信号和脉搏信号均具有规律性强的特征。但泥浆脉冲信号PPM编码信号占空比变化较大,同时还需考虑泥浆脉冲信号噪声干扰的随机性以及信号处理的实时性要求。因此,针对泥浆脉冲信号PPM编码信号的这一特征还需要进一步研究以消除其基线漂移。
2. 泥浆脉冲信号噪声干扰
泥浆脉冲信号以泥浆压力波的形式通过钻柱内从井底传输至地面,能量耗散不可避免,且压力波与其反射波叠加,会产生波形畸变。另外,由于钻头的活动、钻柱的自转公转、钻柱与井壁的撞击、井下工具和泥浆泵的泵冲等干扰因素,接收信号会混叠很强的噪声,为后续信号处理带来困难。图1为现场采集的压力脉冲信号局部特征,采样频率为200 Hz。分析信号的频域特征(图1(b)),噪声分布频域较广,幅度无明显规律,高强度噪声主要集中在0~20 Hz之内,低频噪声中的泵噪信号基值频率接近于0。
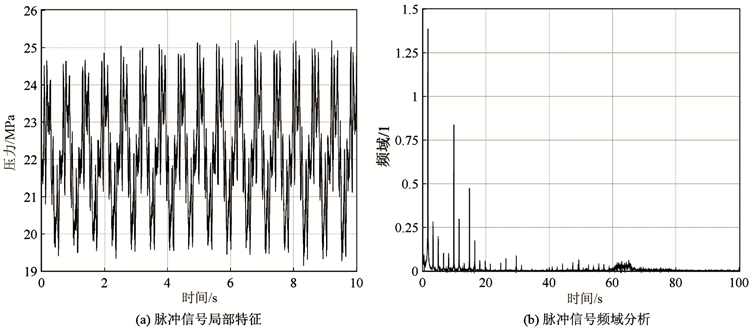
Figure 1. The field acquisition of mud pressure pulse signal and frequency domain analysis of pulse signal
图1. 现场采集泥浆压力脉冲信号及脉冲信号频域分析
3. 形态学滤波
3.1. 形态学运算
地面接收泥浆脉冲信号是一维离散信号,信号序列f(n)定义为
,一维结构元素g(m)定义为
,且M < N。形态学基本运算包括腐蚀和膨胀。
f(n)关于g(m)腐蚀的关系式如下:
,
(1)
f(n)关于g(m)膨胀的关系式如下:
,
(2)
将腐蚀和膨胀进行级联可以组成开运算和闭运算。开运算是指信号先被结构元素腐蚀再膨胀,记为“
”,其关系式为:
(3)
闭运算是指信号先被结构元素膨胀再腐蚀,记为“
”,其关系式为:
(4)
形态学开运算可以抑制信号正脉冲,闭运算可以抑制信号负脉冲,是基本的形态滤波器。
3.2. 形态学滤波器设计
笔者采用2级滤波消除泥浆脉冲信号的基线漂移。第1级形态学滤波器直接处理原始泥浆脉冲信号f0,分别进行先“开”再“闭”运算和先“闭”再“开”运算,并取二者的算术平均,获得信号f1。第1级运算消除高频噪声,保留脉冲信号,选择的结构元素应与脉冲信号特征近似,且结构元素宽度小于脉冲信号宽度。其运算关系式如下:
(5)
第2级形态学滤波器处理第1级运算获得的信号f1,分别进行先“开”再“闭”运算和先“闭”再“开”运算,并取二者的算术平均,获得基线漂移相关分量信号f2。第2级运算需要消除脉冲信号,且保留基线的特征,结构元素宽度应大于脉冲信号的宽度。其运算关系式如下:
(5)
最后,将原始泥浆脉冲信号f0减去基线漂移相关分量信号f2,即可消除原始泥浆脉冲信号的基线漂移。
(6)
4. 试验分析
试验研究采用含强非线性基线漂移的模拟泥浆脉冲信号作为样本,分别采用最小二乘多项式拟合法、中值滤波法和形态学滤波法消除该信号的基线漂移,并对计算结果进行定量分析。
4.1. 试验样本
将基线信号从噪声信号中排除,并单独考虑,作为重要分析对象。图2为理想泥浆脉冲信号和各信号分量。
4.2. 结果分析
4.2.1. 定性分析
采用最小二乘多项式拟合法、中值滤波法和形态学滤波法,分别处理图2中的模拟信号e和f (结果如图3、图4所示)。图3(a)中左端仍可见比较明显的基线波动,图3(b)中左端的基线波动轻微,图3(c)中左端基线波动极小。图4(a)中右端仍存明显的基线波动,图4(b)和图4(c)右端基线波动轻微。因此,可以初步判断形态学滤波消除基线漂移的效果最佳,中值滤波法的效果次之,最小二乘多项式拟合法的效果最差。
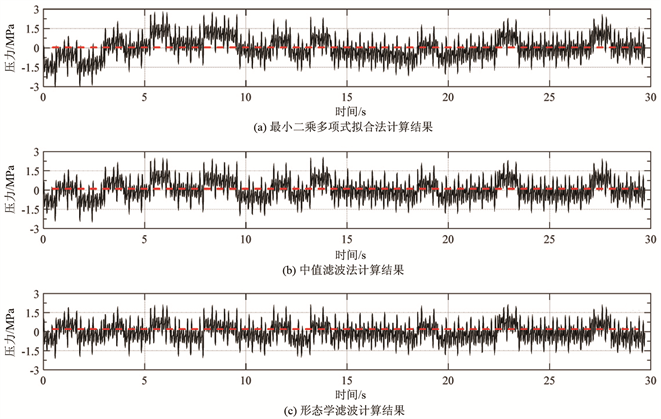
Figure 3. The modified results of strong nonlinear baseline drift at high duty cycle of analog signals
图3. 模拟信号高占空比处存在强非线性基线漂移的修正结果
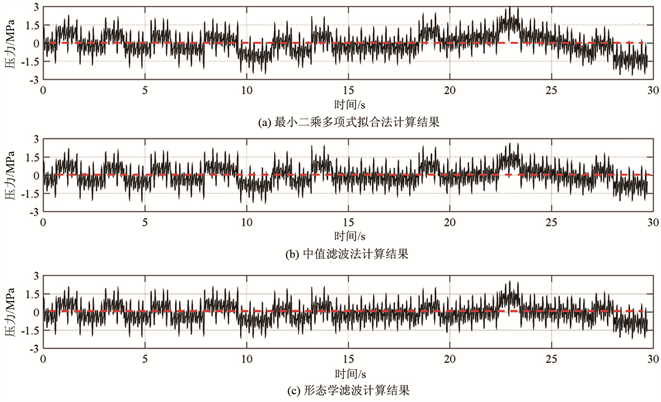
Figure 4. The modified results of strong nonlinear baseline drift at low duty cycle of analog signals
图4. 模拟信号低占空比处存在强非线性基线漂移的修正结果
4.2.2. 定量分析
选取信噪比(RSN)、均方根误差(Erms)、归一化相关系数(Cncc) 3个指标进行定量分析。RSN越大、Erms越小、Cncc越接近1,则表示信号消除基线漂移的效果越好。计算RSN、Erms、Cncc所需的对比样本为图2(c)为例,结果见表1、表2,可以看出,在PPM编码信号占空比高、低两种情况下,形态学滤波结果的RSN最大、Erms最小、Cncc最接近1,所以形态学滤波的效果最好。3种方法对比,中值滤波的效果次之,最小二乘多项式拟合最差。

Table 1. The comparison of modified results of strong nonlinear baseline drift at high duty cycle of analog signals
表1. 模拟信号高占空比处存在强非线性基线漂移的修正结果对比

Table 2. The evaluation of modified results of strong nonlinear baseline drift at low duty cycle of analog signals
表2. 模拟信号低占空比处存在强非线性基线漂移的修正结果评价
5. 结论
采用2级滤波消除泥浆脉冲信号的基线漂移,分别采用最小二乘多项式拟合、中值滤波和形态学滤波处理含强非线性基线漂移的模拟泥浆脉冲信号。对比结果显示,在PPM编码信号占空比高、低两种情况下,形态学滤波的RSN最大、Erms最小、Cncc最接近1,说明形态学滤波可以有效地消除泥浆脉冲信号的基线漂移,效果最佳。