1. 引言
利用风能进行发电是一种非常理想的发电方式,大力发展风力发电,不仅能减轻常规火力发电的压力,也符合当今提倡环保的理念。然而风力发电机的输出功率主要取决于风速的大小,但是风速的大小包含着许多不确定的因素,所以风电机组的大规模并入电网势必会对整个电力系统造成很多方面的影响,尤其是对整个系统的潮流计算 [1] [2] 。
潮流计算是整个电力系统分析的关键所在,它主要的目的就是通过电力系统已知的运行条件(网络结构、元件参数、发电机出力等)分析出整个系统的运行状态,比如系统中的功率分布、功率损耗以及各个节点电压的幅值与相角 [3] 。通过这些数据我们可以了解到整个电力系统是否存在着一些安全隐患,比如电压越限等,以及该系统是否符合经济性的要求 [4] 。现在应用最广泛的是常规的潮流计算,所谓常规的潮流计算是指在系统的发电机出力等条件是已知的情况下进行的潮流计算。常规性的潮流计算主要分为牛顿-拉夫逊法和PQ分解法两种,在这两者基础上又衍生出了许多新的潮流计算方法,但都没有前两者应用广泛 [5] 。由于包含许多不确定因素的风能等清洁能源的并入电网,给整个系统的潮流计算带来了前所未有的压力,此时若采用常规性的潮流计算是无法得出准确的潮流结果的。
因此本文在常规性潮流计算的基础上,提出了一种蒙特卡罗模拟的方法,能够很好的考虑到风电机组在并网时的不确定性,并且收敛速度快,能够满足工程的精度要求。
2. 蒙特卡罗法
蒙特卡罗是一种将统计学与概率学结合起来解决数值统计问题本质属于随机模拟的方法,其基本思想如图1所示 [6] [7] 。
例如,假定ω是随机变量X的数学期望E(X),我们用近似的方法确定ω的步骤是首先对X进行N次独立重复抽样,生成N组X的值,分别为
,其算数平均值为
(1)
根据强大数定理
(2)
当N趋近于无穷大时,
成立的概率为1,所以我们可以用XN来作为
的替代值 [8] 。

Figure 1. The basic idea of montecarlo
图1. 蒙特卡罗基本思想
在本例中,首先按照选定的风速概率密度方程,通过Matlab生成大量符合条件的风速样本,而后利用风速求得风力发电机的有功功率,得到其概率统计特性,最后将风力发电机的出力代入电力系统的某一结点进行潮流计算。该方法生成的样本越多,得到的数据就越准确。
3. 风能模型
3.1. 风速概率模型
风速的概率模型是考虑不确定性的风电场并网潮流计算的一个重要方面,描述风速分布模型的有很多,例如Log-normal分布模型、Gamma分布模型、Burr分布模型、Weibull分布模型等等,其中使用最普遍、与风速切合最好的是遵从两参数分布的Weibull分布模型 [9] [10] ,其概率密度函数
(3)
通过其概率密度函数可以推导出其累积分布函数
(4)
在上述的两式中,c与k分别代表Weibull分布的尺度参数与形状参数,其中c反映的是风电机组的平均风速,v代表的是给定风速,单位是m/s。在本文中,c = 8.0928,k = 2.3466 [11] 。
3.2. 风力发电机输出模型
根据相关数据分析可以得到风力发电机的输出功率随风速变化曲线大致如图2所示 [12] 。
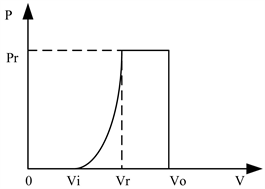
Figure 2. Wind turbine output power curve
图2. 风力发电机输出功率曲线
风力发电机输出功率的表达式
(5)
式中:Pr是风力发电机的最大功率,Vi是切入风速,Vo是切出风速,Vr是风力发电机刚达到最大功率时的风速。
4. 牛顿-拉夫逊法潮流计算
牛顿-拉夫逊法又叫牛顿法,是一种经常被应用在处理非线性问题上的办法,它的本质就是通过用直线代替曲线,将原来非线性的问题逐渐线性化,反复迭代进行求解 [13] 。
当使用直角坐标表示节点电压时
(6)
导纳矩阵元素为
(7)
将上式带入节点功率的方程可得
(8)
(9)
式中:ei与fi为节点电压的实部与虚部,Gij与Bij为节点导纳矩阵的实部与虚部,Pi与Qi分别代表节点的有功功率与无功功率。
设1 − m号节点PQ为节点,Pis与Qis分别为第i节点给定的有功功率和无功功率,由此可得各个节点的功率不平衡方程
(10)
(11)
设m + 1到n − 1号节点为PU节点,此时的不平衡方程
(12)
(13)
根据上述几式可以写出修正方程
(14)
然后通过求解修正方程,将其结果带入上述几式一步步进行牛顿-拉夫逊法迭代,直到计算结果达到给定误差要求,从而求得各个节点电压的幅值与相角以及整个电力系统的潮流分布。
本文具体的潮流计算路线如图3所示。
5. 算例分析
本文的分析建立在IEEE14节点系统上,其中平衡节点为1号节点,风电场接入节点为14号节点,系统的基准容量为100 MVA,其系统结构如图4所示。
风力发电机单机参数如表1所示。

Table 1. Single wind turbine parameters
表1. 单机参数
根据第2节讲述的蒙特卡罗思想,生成的样本数量越多,误差越小,得到的结果越准确。但在实际操作中是不现实的,因为这样会导致计算极其繁琐。所以本文的模拟误差精度取0.01,通过文献 [14] 可以得到模拟的次数为1024次,因此利用Matlab生成了1024组风速,其风速期望值、风力发电机输出功率期望值及其两者的标准差如表2所示。

Table 2. Expected value and standard deviation of wind speed and output power
表2. 风速及输出功率的期望值与标准差
将上述的风力发电机的输出功率期望值带入风电节点进行潮流计算,假定每台发电机的输出功率与功率因数一致,其中功率因数取0.90。为了能够凸显不同风机容量下的潮流结果,本文选取了三组分别为10台、50台、80台的风力发电机数作为对比,各个节点电压幅值(标幺值)与相角的潮流计算结果如表3所示,计算精度取0.0001。

Table 3. Power flow calculation results
表3. 潮流计算结果
从表3可以看出,在潮流计算结果中,距离风电机组并网节点较近的节点如9、13号节点的电压受其影响较大,距离风电机组并网节点较远的节点如2、3号节点受其影响不明显。
6. 结论
随着人们环保理念的提高,风力发电等清洁能源的大规模发展成为了必然的趋势,所以含风力发电的电力系统潮流计算就成为了大规模风电并网的基础与关键。本文通过对风能模型的分析,提出了一种风速不确定时的风电场潮流计算,该方法计算精度高,考虑了风速上下波动对风力发电机的影响,并且通过三组含不同台数含风力发电机的节点系统验证了本方法的可行性与准确性。计算分析结果表明,本文给出的潮流计算方法正确有效,具有良好的鲁棒性,并且从中可以看出风电场功率的大小以及风电场并网节点的选取会对整个电力系统产生或多或少的影响,对以后大规模的风电并网潮流计算有很好的参考价值。
基金项目
国家级大学生创新训练项目,项目编号:201810429202,201810429220。