刚体空间运动的动力学方程的联合推导

United Derivation of Dynamical Equations for Rigid Body Spatial Motion

摘要: 本文推导出相对任意基点刚体动力学方程的一种更简洁的形式。推导过程是以质点系动力学理论为基础的，它是一个比动量定理和角动量定理更基本的理论前提。在现有的动力学方程中，线加速度和角加速度是相互耦合的，这导致了求解方程极其困难，特别是在高速旋转的条件下。本文通过平移方程和旋转方程的联立推导，将线加速度和角加速度解耦。基于推导过程，讨论了与现有形式的关联，陈述了与现有推导过程的主要差异。

Abstract: Dynamical equations for rigid body spatial motion are derived from Dynamical equations of system of particles, which is a more fundamental theoretical basis than the momentum theorem and angular momentum theorem. Linear acceleration and angular acceleration are coupled with each other in the present dynamical equations which lead to solve the equation is extremely difficult, especially under conditions of high speed rotation. The derivation coupled the translational for-mulation and the rotational formulation, and uncoupled the linear acceleration and angular ac-celeration. Based on the derivation process, the relationship between the equations and the exist-ing forms is discussed; the main differences from the existing derivation process are stated.

1. 引言

刚体空间一般运动的动力学描述 [1] ，是由平移(动力学)方程和旋转(动力学)方程等两个方程的“组合”来进行描述的，平移方程和旋转方程合称为描述刚体一般运动的刚体动力学方程。

刚体动力学方程的形式推导大致经历了三个阶级。第一阶段，动力学方程由惯性参考系中描述质点系质心平移运动的质心运动定理 [2] ，和连体参考系中描述刚点定点旋转运动的坐标形式的欧拉方程进行组合来进行描述的 [3] [4] 。第二阶段，Wittenburg [5] 推导出惯性系中基于任意基点的旋转方程。这样，平移方程和旋转方程就都可以在惯性系中进行统一描述。第三阶段，Featherstone [6] 、李洲圣 [7] 推导了惯性系中基于任意点的平移方程。

由于线加速度和角加速度的耦合，第三阶段推导出的方程很难直接应用于多刚体动力学的建模，目前的主流方法 [8] 是将其整体转换到连体参考系中进行求解。将惯性系的原点平移至质心处，将线加速度和角加速度进行解耦，也是一种较为常用的途径 [9] 。但是，这种形式的方程不利于定点陀螺、翻身陀螺、陀螺仪等刚体的数值求解 [7] 。本文将推导惯性系下基于任意基点的解耦的动力学方程。

2. 质点系动力学方程概要

质点系是指由许多个相互联系着的质点所组成的系统 [2] 。沈惠川和李书民 [2] 对质点系进行了极为精炼的表述。

考虑一个惯性系，其坐标系的原点标记为O。将惯性系作为相对静止的参考系，研究质点系相对于惯性系的运动。质点系中的全部质点标记为 $k\left(k=1,2,3,\cdots \right)$ ，质点k的位置用矢量形式描述为r_ok；质点k所受的外力为F_k。其中，r_ok的下标o表示矢量的起点，k表示矢量的终点，两个点都是物质点。F_k的下标k表示矢量的起点，终点是无物质点标注的。这种标记格式是本文的默认格式。质点的速度和加速度定义为

${\stackrel{\dot{}}{r}}_{ok}=v_k$ (1)

${\stackrel{\dot{}}{v}}_k=a_k$ (2)

推导质点系动量定理和角动量定理的动力学方程 [2] 为

${\displaystyle \underset{k}{\sum }{m}_k{a}_k}={\displaystyle \underset{k}{\sum }{F}_k}$ (3)

${\displaystyle \underset{k}{\sum }\left(r_{ok}\times m_k{a}_k\right)}={\displaystyle \underset{k}{\sum }\left(r_{ok}\times F_k\right)}$ (4)

质点系力学中引入了质心的概念，其定义为

$m{r}_{oc}={\displaystyle \underset{k}{\sum }{m}_k{r}_{ok}}$ (5)

式中，m_k为质点k的质量，r_oc为从惯性系原点O至质心C的矢量，m为质点系的总质量，即

$m={\displaystyle \underset{k}{\sum }{m}_k}$ (6)

3. 刚体动力学方程

本节将从式(3)和(4)出发，推导刚体一般运动的动力学方程。

3.1. 质点位置的分解

刚体是一种简化的质点系模型。刚体简化表述为：质点系内部的任意两个质点之间的距离都保持不变的 。这样，在刚体内部任意选择一个基点i，质点k (k = 1, 2, 3, ∙∙∙)的位置矢量可以分解为两个部分

$r_{ok}=r_{oi}+{\rho }_{ik}$ (7)

式中，r_oi的长度随时而变，而ρ_ik的长度不随时而变。在本文中约定，长度不变的矢量均采用ρ来表示。为了利用质心定义来化简方程，ρ_ik进行二次分解

${\rho }_{ik}={\rho }_{ic}+{\rho }_{ck}$ (8)

这样，在惯性系内部，质点k的位置表示为

$r_{ok}=r_{oi}+{\rho }_{ic}+{\rho }_{ck}$ (9)

将r_ok代入式(5)化简，得到一个关键的化简公式

${\displaystyle \underset{k}{\sum }{m}_k{\rho }_{ck}}=0$ (10)

在惯性系内部，刚体关于质心C点的转动惯量为

(11)

式中，[ρ_ck]_×为ρ_ck叉积运算对应的反对称矩阵左乘运算。

3.2. 质点速度与加速度的分解

基于Possion公式 [2] 定义的角速度，任意长度不变的矢量对时间求导，有

$\begin{array}{l}{\stackrel{\dot{}}{\rho }}_{ik}=\omega \times {\rho }_{ik}\\ {\stackrel{\dot{}}{\rho }}_{ic}=\omega \times {\rho }_{ic}\\ {\stackrel{\dot{}}{\rho }}_{ck}=\omega \times {\rho }_{ck}\end{array}\}$ (12)

将式(9)两端对时间求导，得到质点速度的分解式

$v_k=v_i+\omega \times \left({\rho }_{ic}+{\rho }_{ck}\right)$ (13)

将上式两端再次求导，得到质点加速度的分解式

$a_k=a_i+\stackrel{\dot{}}{\omega }\times \left({\rho }_{ic}+{\rho }_{ck}\right)+\omega \times \left[\omega \times \left({\rho }_{ic}+{\rho }_{ck}\right)\right]$ (14)

按式(13)和(14)的推导过程，易推导出基点i和质心C点的加速度关系

$a_c=a_i+\stackrel{\dot{}}{\omega }\times {\rho }_{ic}+\omega \times \left(\omega \times {\rho }_{ic}\right)$ (15)

3.3. 刚体动力学方程推导

首先，基于式(3)对式(4)进行化简。将式(9)代入式(4)，有

${\displaystyle \underset{k}{\sum }\left[\left(r_{oi}+{\rho }_{ic}+{\rho }_{ck}\right)\times m_k{a}_k\right]}={\displaystyle \underset{k}{\sum }\left[\left(r_{oi}+{\rho }_{ic}+{\rho }_{ck}\right)\times F_k\right]}$ (16)

叉积满足分配律，有

$\begin{array}{l}{r}_{oi}\times \left({\displaystyle \underset{k}{\sum }{m}_k{a}_k}\right)+{\rho }_{ic}\times \left({\displaystyle \underset{k}{\sum }{m}_k{a}_k}\right)+{\displaystyle \underset{k}{\sum }\left({\rho }_{ck}\times m_k{a}_k\right)}\\ =r_{oi}\times \left({\displaystyle \underset{k}{\sum }{F}_k}\right)+{\rho }_{ic}\times \left({\displaystyle \underset{k}{\sum }{F}_k}\right)+{\displaystyle \underset{k}{\sum }\left({\rho }_{ck}\times F_k\right)}\end{array}$ (17)

用r_oi和ρ_ic分别叉乘式(3)的等号两端，有

$r_{oi}\times \left({\displaystyle \underset{k}{\sum }{m}_k{a}_k}\right)=r_{oi}\times \left({\displaystyle \underset{k}{\sum }{F}_k}\right)$ (18)

${\rho }_{ic}\times \left({\displaystyle \underset{k}{\sum }{m}_k{a}_k}\right)={\rho }_{ic}\times \left({\displaystyle \underset{k}{\sum }{F}_k}\right)$ (19)

将式(18)和式(19)代入式(17)，化简得

${\displaystyle \underset{k}{\sum }\left({\rho }_{ck}\times m_k{a}_k\right)}={\displaystyle \underset{k}{\sum }\left({\rho }_{ck}\times F_k\right)}$ (20)

其次，推导刚体基于任意基点i的平移动力学方程。将式(14)代入式(3)，有

${\displaystyle \underset{k}{\sum }{m}_k\left\{a_i+\stackrel{\dot{}}{\omega }\times \left({\rho }_{ic}+{\rho }_{ck}\right)+\omega \times \left[\omega \times \left({\rho }_{ic}+{\rho }_{ck}\right)\right]\right\}}={\displaystyle \underset{k}{\sum }{F}_k}$ (21)

叉积满足分配律，有

$\begin{array}{l}\left({\displaystyle \underset{k}{\sum }{m}_k}\right)\left[a_i+\stackrel{\dot{}}{\omega }\times {\rho }_{ic}+\omega \times \left(\omega \times {\rho }_{ic}\right)\right]\\ +\stackrel{\dot{}}{\omega }\times \left({\displaystyle \underset{k}{\sum }{m}_k}{\rho }_{ck}\right)+\omega \times \left[\omega \times \left({\displaystyle \underset{k}{\sum }{m}_k}{\rho }_{ck}\right)\right]={\displaystyle \underset{k}{\sum }{F}_k}\end{array}$ (22)

将式(6)和(10)代入上式化简，得到刚体基于点i的平移动力学方程

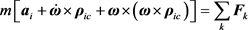(23)

最后，推导刚体的旋转动力学方程。将式(14)代入式(20)，得

${\displaystyle \underset{k}{\sum }\left({\rho }_{ck}\times m_k\left(a_i+\stackrel{\dot{}}{\omega }\times \left({\rho }_{ic}+{\rho }_{ck}\right)+\omega \times \left(\omega \times \left({\rho }_{ic}+{\rho }_{ck}\right)\right)\right)\right)}={\displaystyle \underset{k}{\sum }\left({\rho }_{ck}\times F_k\right)}$ (24)

叉积满足分配律，有

$\begin{array}{l}\left({\displaystyle \underset{k}{\sum }{m}_k{\rho }_{ck}}\right)\times \left(a_i+\stackrel{\dot{}}{\omega }\times {\rho }_{ic}+\omega \times \left(\omega \times {\rho }_{ic}\right)\right)\\ +{\displaystyle \underset{k}{\sum }\left(m_k{\rho }_{ck}\times \left(\stackrel{\dot{}}{\omega }\times {\rho }_{ck}\right)\right)}+{\displaystyle \underset{k}{\sum }\left(m_k{\rho }_{ck}\times \left(\omega \times \left(\omega \times {\rho }_{ck}\right)\right)\right)}\\ ={\displaystyle \underset{k}{\sum }\left({\rho }_{ck}\times F_k\right)}\end{array}$ (25)

式(25)左端第一项，将式(10)代入后，得零。式(25)左端第二项，将ρ_ck叉积运算转换成对应的反对称矩阵左乘运算，得

${\displaystyle \underset{k}{\sum }\left(m_k{\rho }_{ck}\times \left(\stackrel{\dot{}}{\omega }\times {\rho }_{ck}\right)\right)}=I_c\stackrel{\dot{}}{\omega }$ (26)

式(26)左端第三项，利用Jacobi恒等式，有

(27)

将上式代入式(26)左端第三项

$$ (28)

将式(26)和式(28)代入式(25)，得到刚体旋转动力学方程

$I_c\stackrel{\dot{}}{\omega }+\omega \times \left(I_c\omega \right)={\displaystyle \underset{k}{\sum }\left({\rho }_{ck}\times F_k\right)}$ (29)

联立式(23)和式(29)，得到惯性系中基于任意基点i的描述刚体空间一般运动的动力学方程

$m\left[a_i+\stackrel{\dot{}}{\omega }\times {\rho }_{ic}+\omega \times \left(\omega \times {\rho }_{ic}\right)\right]={\displaystyle \underset{k}{\sum }{F}_k}$ (30a)

$I_c\stackrel{\dot{}}{\omega }+\omega \times \left(I_c\omega \right)={\displaystyle \underset{k}{\sum }\left({\rho }_{ck}\times F_k\right)}$ (30b)

将式(15)代入式(30a)，得到惯性系中基于任意基点i的描述刚体空间一般运动的动力学方程的更简洁形式

$a_c=a_i+\stackrel{\dot{}}{\omega }\times {\rho }_{ic}+\omega \times \left(\omega \times {\rho }_{ic}\right)$ (31a)

$m{a}_c={\displaystyle \underset{k}{\sum }{F}_k}$ (31b)

$I_c\stackrel{\dot{}}{\omega }+\omega \times \left(I_c\omega \right)={\displaystyle \underset{k}{\sum }\left({\rho }_{ck}\times F_k\right)}$ (31c)

4. 讨论

4.1. 与现有方程的关系

式(30a)是Featherstone [6] 和李洲圣 [7] 推导的平移方程的形式。将式(30a)简化为基于质心点的形式(31b)的推导过程，现有推导过程的方式是：在惯性系中新建一个参考系(标记为rfB)，rfB的坐标系原点固定在刚体的质心点处，rfB的坐标系的3个基矢量平行于惯性系的3个基矢量。由于刚体的质心点是一个(相对于原惯性系的)运动的物质点，所以，rfB是一个(相对于原惯性系的)运动着的参考系。式(31a)和(31b)联立的实质是：不需要在原惯性系中建立一个新的运动着的参考系，这两式的联立就可以描述原惯性系中刚体基于任意基点i的平移运动。

式(31c)通常被认为只在rfB中才能成立。惯性系中基于任意基点i，Wittenburg [5] 推导的形式为

${\rho }_{ic}\times m{a}_i+I_i\stackrel{\dot{}}{\omega }+\omega \times \left(I_i\omega \right)={\rho }_{ic}\times \left({\displaystyle \underset{k}{\sum }{F}_k}\right)+{\displaystyle \underset{k}{\sum }\left({\rho }_{ck}\times F_k\right)}$ (32)

式中，I_i为惯性系中刚体关于矩心i的转动惯量。式(32)与Wittenburg的公式的写法区别在于：Wittenburg将式(32)的右端简记为(关于矩心i的)力矩符号。根据转动惯量在矩心点i和矩心点c之间的切换公式

$I_i=-m{\left[{\rho }_{ic}\right]}_{\times }^2+I_c$ (33)

将上式代入式(32)，得到Featherstone [6] 和李洲圣 [7] 推导的形式

$\begin{array}{l}{\rho }_{ic}\times m{a}_i+\left(I_c-m{[{\rho }_{ic}]}_{\times }^2\right)\stackrel{\dot{}}{\omega }+\omega \times \left(\left(I_c-m{[{\rho }_{ic}]}_{\times }^2\right)\omega \right)\\ ={\rho }_{ic}\times \left({\displaystyle \underset{k}{\sum }{F}_k}\right)+{\displaystyle \underset{k}{\sum }\left({\rho }_{ck}\times F_k\right)}\end{array}$ (34)

式中，为[ρ_ic]_×和[ρ_ic]_×的矩阵乘积。将式(34)进行重新整理，得

$\begin{array}{l}{\rho }_{ic}\times m{a}_i-m{\left[{\rho }_{ic}\right]}_{\times }^2\stackrel{\dot{}}{\omega }-m\omega \times \left({\left[{\rho }_{ic}\right]}_{\times }^2\omega \right)+I_c\stackrel{\dot{}}{\omega }+\omega \times \left(I_c\omega \right)\\ ={\rho }_{ic}\times \left({\displaystyle \underset{k}{\sum }{F}_k}\right)+{\displaystyle \underset{k}{\sum }\left({\rho }_{ck}\times F_k\right)}\end{array}$ (35)

将[ρ_ic]_×运算转换为ρ_ic叉乘运算，式(35)的第一、二和三项可变形为

$\begin{array}{l}{\rho }_{ic}\times m{a}_i-m{\left[{\rho }_{ic}\right]}_{\times }^2\stackrel{\dot{}}{\omega }-m\omega \times \left({\left[{\rho }_{ic}\right]}_{\times }^2\omega \right)\\ ={\rho }_{ic}\times m\left[a_i+\stackrel{\dot{}}{\omega }\times {\rho }_{ic}+\omega \times \left(\omega \times {\rho }_{ic}\right)\right]\end{array}$ (36)

用ρ_ic叉乘式(30a)的两端，有

${\rho }_{ic}\times m\left[a_i+\stackrel{\dot{}}{\omega }\times {\rho }_{ic}+\omega \times \left(\omega \times {\rho }_{ic}\right)\right]={\rho }_{ic}\times \left({\displaystyle \underset{k}{\sum }{F}_k}\right)$ (37)

将式(36)代回式(35)，并利用式(37)进行化简，得

$I_c\stackrel{\dot{}}{\omega }+\omega \times \left(I_c\omega \right)={\displaystyle \underset{k}{\sum }\left({\rho }_{ck}\times F_k\right)}$ (38)

显然，式(38)就是式(31c)，Featherstone和李洲圣的旋转方程形式，在满足式(37)的前提下，与(31c)是等价的。通过推导可以发现，在满足式(31a)和式(31b)的前提下，Wittenburg、Featherstone和李洲圣的旋转方程都可以进一步化简为更为简洁的式(31c)的形式。因此，式(31c)并非只在rfB中才能成立，当它与式(31a)和式(31b)联立时，在惯性系中也是成立的。

4.2. 与现有推导的主要差异

现有推导过程多种多样，本小节仅讨论本文推导过程的独特之处。

首先，现有推导过程主要是从质点系的动量定理和角动量定理为出发点的，而质点系动量定理和角动量定理的推导是以质点系动力学方程(3)和(4)为出发点，而本文推导过程是直接以质点系动力学方程(3)和(4)为出发点的，绕开了质点系动量定理和角动量定理。

其次，现有推导过程中，物质点的位置矢量r和ρ的右下标的标记采用了简化形式，仅标记了矢量的终点；而本文推导时矢量的标记采用起点和终点同时标记的形式。当一个矢量不标记起点时，它的默认起点的坐标系的原点，这使描述刚体运动的基点从任意点i向质心C点切换时，需要新建一个rfB参考系。本文的推导过程只需要一个参考系，即静止的惯性参考系。

最后，本文的推导过程没有引入力矩的概念，现有推导过程大多都使用了力矩的概念。力矩的量值与矩心的选择有关，力矩在不同矩心之间可以采用切换公式进行转换。没有使用力矩概念，使本文的推导过程不需要使用切换公式，也使平移方程和旋转方程之间的关联性更为清晰。这个特点主要体现在式(18)、式(19)和式(37)的推导中。

4.3. 刚体一般运动的表述方式

通常，刚体空间一般运动表述为 [10] ：随基点i的平移运动和绕基点i的旋转运动的合成(或组合)。其中，“合成”或“组合”的语义表述，包括着平移运动和旋转运动是两种相互独立的运动形式，只有通过同一个基点，才能完整地描述刚体的一般运动。正是基于这种思路，Featherstone和李洲圣推导动力学方程，都是采用了单一的、非质心的基点来描述刚体的一般运动。其结果是，线加速度量和角加速度量是相互耦合的。

事实上，刚体的旋转运动与基点是无关的，角加速度量是无需与线运动量进行耦合的。本文从关联性角度推导的动力学方程，线加速度与角加速度是解耦的，两者的联系只在于共同确定着刚体内任意一点i的线加速度(即式(31a))。很多学者 [11] [12] [13] [14] 讨论和证明了，刚体的角加速度与基点的选择是无关的。这意味着，不论选择的基点如何选择，动力学方程式(31)、式(32)和式(34)解算出的角加速度值是一致的。所以，旋转运动与基点的选择是无关的，刚体空间一般运动可以更清晰的表述为：旋转运动和随任意基点i的平移运动的联合。

5. 结束语

在惯性系下，本文推导了刚体空间一般运动的动力学方程的更简洁的解耦形式。推导过程从质点系动力学方程出发，推导过程比较清晰。通过讨论，梳理了现有的两种方程的形式之间的关联和区别。

刚体动力学方程是一个非线性的常微分方程。既使在解耦的前提下，数值求解的困难也很大。目前，在多体动力学研究领域主要采用了耦合形式的动力学方程，这使得数值积分的精确度很难得到满足，特别是面对长时间、高速转动的工程问题时。本文推导的解耦形式，对于长时间、高速转动等工程问题的更精确数值求解提供了理论基础。