室内移动测图平台的多传感器联合标定

Extrinsic Calibration of Multi LiDAR-Camera Robotic System for Indoor Mapping

摘要: 室内移动测图平台集成多目相机、二维激光扫描仪等多种传感器，用以实现室内的高精度定位及三维空间数据获取。精确标定出传感器的外参数，实现传感器空间基准统一，这是多传感器数据有效利用的基础，也是室内测图平台相关研究的重点问题之一。本文提出一种便捷的多目相机及二维扫描仪的标定方法，首先，在平台上布设控制，建立机身坐标系。然后在相机与扫描仪的有效视场分别布设黑白靶标、靶球作为公共点，借助于高精度三维激光扫描仪获取公共点在机身坐标系中坐标值。接着使用EPNP算法进行相机的标定，圆拟合的方法实现扫描仪标定，获取传感器在机身坐标系下外参数。最后对标定实验结果进行精度验证，相机标定重投影误差低于1个像素，扫描仪标定结果优于1厘米。

Abstract: Multi LiDAR-camera is integrated on the indoor mapping robotic system for mission of high-precision positioning and three-dimensional spatial data acquisition. Accurate extrinsic calibration of sensors is the basis of effective utilization of multi-sensors data, and is also one of key issues of indoor mobile mapping research. This paper presents a convenient calibration method for multi-sensors. First, some control points are laid on the body of the robot to create the robot body coordinate system. Then, several identifiable targets are fixed in the effective field of view of LiDAR and camera. The coordinate value of targets in the robot body coordinate system is obtained by three-dimensional laser scanner. Finally, EPNP algorithm is used to calculate the extrinsic of camera based on the corresponding relationship between two-dimensional points and three-dimensional points, and RANSAC circle fitting is used to calibrate the 2D LiDAR. Experiments show that the camera reprojection error is less than 1 pixel and the calibration result of 2D LiDAR is better than 1 cm.

1. 引言

室内封闭环境下实现高精度定位和三维成图是当今移动测量领域的热点研究问题。为解决这些问题，激光和视觉传感器作为主要传感器集成在室内移动测量系统中。相机可获取环境中的纹理及色彩信息，激光可以采集高精度的空间位置信息，这两种传感器的组合实现优势互补 [1] 。

同种传感器由于安置位置与姿态的不同，获取到的数据在空间基准存在差异。相机及扫描仪这两种不同类型的传感器由于几何参考框架上的不同，获取的光学影像与激光点云是二种跨模态(cross-modal)异源数据，这两类数据在精准对准上仍存在困难 [2] 。传感器外参数的精确标定，可确定传感器的位置与姿态。借助标定得到的外参数可以实现不同传感器在空间基准上的对齐，为多相机交会测量以及多源数据融合等相关工作提供先验信息。

相机由于缺乏深度信息，其外参数标定需要依赖于三维空间点坐标与其二维图像坐标间的对应关系 [3] 。目前最常用的方法是PnP (Perspective-N-Point)方法，以三维空间坐标和像素坐标为基础构建方程，求解相机的位置与姿态，经典的算法包括直接线性变换、P3P以及P4P [4] [5] 。其中EPnP算法是Lepetit提出的相机位姿解算方法，该方法具有更高的抗干扰能力，能够更精准地计算出相机的位姿参数 [6] [7] 。

对于相机与激光间的外参标定，文献 [8] [9] 在3D激光扫描仪与相机视场重叠的情况下，找寻公共点，通过直接线性变换的方式，解算相机在激光坐标系下的位置与姿态。相比三维激光扫描仪，二维扫描仪获取的是扫描面的二维数据，且一个位置姿态下只能获取一个扫描面的点云数据，公共点的缺乏给传感器间联合标定增加了难度 [10] 。文献 [11] [12] 在二维扫描仪与相机的公共视场下摆放棋盘格，基于点与面间的几何约束解算传感器间的相对外参数。但是在传感器视场无重叠情况下，由于缺乏充足的公共点，多传感器外参数标定仍存在困难。

针对室内测图平台上搭载的工业相机及二维扫描仪等传感器的外参标定需求，本文提出一种传感器联合标定的方法。首先，在平台上布设控制点建立机身坐标系，以此为基准进行传感器的联合标定。接着，在传感器的有效视场下布设公共点，获取公共点在传感器坐标系与机身坐标系下的坐标。最后分别使用EPNP算法和共线方程解算出相机与断面扫描仪的外参数，借助于解算得到的外参数可实现传感器坐标系与机身坐标系之间的空间基准转换。

2. 传感器联合标定方法

室内测图平台的外参数标定涉及到多个不同类型传感器，为便捷实现多传感器间外参数的精确标定，在该平台上布设控制点建立机身坐标系。以机身坐标系为基准展开传感器外参数标定，求得传感器坐标系与机身坐标系间的转换参数，从而建立传感器数据空间基准上的关联。传感器的标定流程如图1所示。

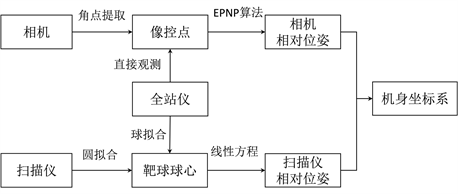
Figure 1. Flow chart of extrinsic calibration for Indoor Mapping Robot

图1. 移动测图平台传感器标定流程图

2.1. 坐标系定义及坐标系转换参数计算

为了更好描述标定方法，逐一介绍设计到的坐标系，坐标系示意图如图2所示。

Figure 2. Schematic diagram of sensor coordinate system

图2. 传感器坐标系示意图

1) 相机坐标系：以相机的投影中心为坐标原点，X轴向右，Y轴向下，Z轴向右构成笛卡尔右手坐标系，使用 $p_i^c\left(x_i^c,y_i^c,z_i^c\right)$ 表示相机坐标系下坐标。

2) 扫描仪坐标系：以扫描仪的激光发射中心为坐标原点，X轴向右，Y轴向前，Z轴向上构成笛卡尔右手坐标系，使用 $p_i^l\left(x_i^l,y_i^l,z_i^l\right)$ 表示扫描仪坐标系下坐标。

3) 机身坐标系：为自定义坐标系，其中X轴向右，Y轴向前，Z轴向上构成笛卡尔右手坐标系，在文中使用 $p_i^b\left(x_i^b,y_i^b,z_i^b\right)$ 表示该坐标系下坐标系。

两个三维笛卡尔坐标系间转换参数包括3个旋转参数与3个平移参数。以机身坐标系与激光坐标系间坐标转换为例，可以用公式(1)进行表示，获取三个或以上公共点即可构造共线方程进行解算。

$p_i^b=R\left(A_x,A_y,A_z\right)\left[\begin{array}{c}\begin{array}{c}{x}_i^l\\ y_i^l\\ z_i^l\end{array}\end{array}\right]+\left[\begin{array}{c}\begin{array}{c}{t}_1^l\\ t_2^l\\ t_3^l\end{array}\end{array}\right]$ (1)

其中 $T\left(t_1^l,t_2^l,t_3^l\right)$ 和R分别为传感器坐标系到机身坐标系的平移矩阵和旋转矩阵。R由三个旋转角 $A_x,A_y,A_z$ 构成，当坐标轴依次按照x轴、y轴、z轴的顺序逆时针旋转 $A_x,A_y,A_z$ 三个角度值时，则R可以用公式(2)表示，当旋转顺序发生变化时R的计算式发生改变。

$R=\left[\begin{array}{ccc}\cos A_z& -\sin A_z& 0\\ -\sin A_z& \cos A_z& 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{ccc}\cos A_y& 0& -\sin A_y\\ 0& 1& 0\\ -\sin A_y& 0& \cos A_y\end{array}\right]\left[\begin{array}{ccc}1& 0& 0\\ 0& \cos A_x& \sin A_x\\ 0& -\sin A_x& \cos A_x\end{array}\right]$ (2)

2.2. 相机外参数标定

从相片获取像控点的像素坐标 $\left(u_i,v_i\right)$ ，在三维扫描仪获取的点云中获取像控点在机身坐标系下坐标 $\left(x_i^b,y_i^b,z_i^b\right)$ ，基于三维点坐标与二维像素坐标间的对应关系，借助EPNP方法解算相机的外参数。

使用四个不共面的虚拟坐标 $\left(x_i^{cb},y_i^{cb},z_i^{cb}\right),i=1,2,3,4$ 表示像控点在机身坐标系下的坐标，如公式(3)进行表示，类似的在相机坐标系下坐标也可以同样以该坐标系下四个虚拟坐标，如公式(4)进行表示。

$p_j^l={\displaystyle {\sum }_{i=1}^4{W}_{i,j}{c}_i^{pb}}$ (3)

$p_j^c={\displaystyle {\sum }_{i=1}^4{W}_{i,j}{c}_i^{pc}}$ (4)

两个三维笛卡尔坐标系间进行坐标系转换过程中，表示空间点的四个虚拟点的权重 $W_{i,j}$ 始终不变。故计算得到虚拟点点在相机坐标系下坐标，即可以解算出相机坐标系与机身坐标系间的转换参数。借助于相机内参数矩阵，可以实现相机坐标系与像素坐标间的转换，转换公式如公式(5)所示。

$z_i^c\left[\begin{array}{c}{u}_i\\ v_i\\ 1\end{array}\right]=\left[\begin{array}{ccc}{f}_u& 0& u_c\\ 0& f_v& v_v\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}{x}_i^c\\ y_i^c\\ z_i^c\end{array}\right]$ (5)

$f_u$ 与 $f_v$ 为相机焦距， $u_c$ 与 $v_v$ 为主点坐标。结合公式(4)，则公式(5)可以表示成：

$z_i^c\left[\begin{array}{c}{u}_i\\ v_i\\ 1\end{array}\right]=\left[\begin{array}{ccc}{f}_u& 0& u_x\\ 0& f_c& v_y\\ 0& 0& 1\end{array}\right]{\displaystyle {\sum }_{i=1}^4{W}_{i,j}\left[\begin{array}{c}{x}_i^{pc}\\ y_i^{pc}\\ z_i^{pc}\end{array}\right]}$ (6)

基于像控点的像素坐标系及对应虚拟点的权重，可组建方程如公式(7)所示，n个像控点则可以构建行数为2 × n的线性方程组。4个虚拟点在机身坐标系下坐标已知，借助于奇异值分解的方法解求方程组，可获得其在相机坐标系下坐标，借助公式(1)计算可得到相机的外参数。

$\{\begin{array}{l}{\displaystyle {\sum }_{j=1}^4{W}_{i,j}{f}_u{x}_i^{pc}}+W_{i,j}\left(u_c-u_i\right)z_i^c=0\\ {\displaystyle {\sum }_{j=1}^4{W}_{i,j}{f}_u{x}_i^{pc}}+W_{i,j}\left(u_c-u_i\right)z_i^c=0\end{array}$ (7)

2.3. 扫描仪外参数标定

标定扫描仪需要3个以上公共点，获取公共点在激光坐标系与机身坐标系下的坐标，经共线方程解算求得两种坐标系间转换参数。二维扫描仪的标定过程如图3所示，以靶球球心作为公共点，作为扫描仪标定的参考点。激光的扫描面与靶球表面相交，交线为图3中待拟合圆中一段圆弧。

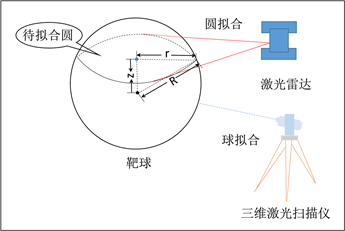
Figure 3. Extrinsic calibration of 2D LiDAR

图3. 激光外参数标定

待拟合圆的圆心与靶球球心的连线垂直于扫描仪扫描面，其距离值为激光坐标系下球心的Z坐标。为剔除采集过程中产生的噪点，采用RANSAC圆拟合的方法进行圆方程拟合。该拟合方法主要有以下几个步骤：1) 从圆弧段点云中，随机选取3个点进行圆拟合，获得圆方程。2) 计算其余点距离拟合得到圆的距离，小于设定的阈值则认为该点是局内点，记录下局内点的点数。3) 循环以上两个步骤，局内点最多的方程为最佳圆拟合方程。

圆拟合得到圆心坐标(x，y)以及该圆的半径r，靶球半径R已知，则球心点在激光坐标系下的 $Z_l$ 坐标可以通过公式计算得到。

$\left|Z_l\right|=\sqrt{R^2-r^2}$ (8)

三维激光扫描仪获取靶球表面点在机身坐标系下的三维坐标信息，球的空间方程可设为：

$x^2+y^2+z^2-Ax-By-Cz+D=0$ (9)

圆心坐标系为 $\left(A/2,B/2,C/2\right)$ ，将三维扫描仪测得点位坐标带入上式，构建共线方程组，

$\left[\begin{array}{cccc}{x}_1& y_1& z_1& -1\\ ⋮& ⋮& ⋮& ⋮\\ x_n& y_n& z_n& -1\end{array}\right]\left[\begin{array}{c}A\\ B\\ C\\ D\end{array}\right]=\left[\begin{array}{c}{x}_1^2+y_1^2+z_1^2\\ ⋮\\ x_n^2+y_n^2+z_n^2\end{array}\right]$ (10)

利用最小二乘可解得球方程，结果如式(11)所示，

$\left[\begin{array}{c}A\\ B\\ C\\ D\end{array}\right]={\left[\begin{array}{cccc}{\displaystyle \sum x_i^2}& {\displaystyle \sum x_i{y}_i}& {\displaystyle \sum x_i{z}_i}& -{\displaystyle \sum x_i}\\ {\displaystyle \sum x_i{y}_i}& {\displaystyle \sum x_1^2}& {\displaystyle \sum y_i{z}_i}& -{\displaystyle \sum y_i}\\ {\displaystyle \sum x_i{z}_i}& {\displaystyle \sum y_i{z}_i}& {\displaystyle \sum x_1^2}& -{\displaystyle \sum z_i}\\ -{\displaystyle \sum x_i}& -{\displaystyle \sum y_i}& -{\displaystyle \sum z_i}& n\end{array}\right]}^{-1}\left[\begin{array}{c}{\displaystyle \sum x_i\left(x_i^2+y_i^2+z_i^2\right)}\\ {\displaystyle \sum y_i\left(x_i^2+y_i^2+z_i^2\right)}\\ {\displaystyle \sum z_i\left(x_i^2+y_i^2+z_i^2\right)}\\ {\displaystyle \sum -\left(x_i^2+y_i^2+z_i^2\right)}\end{array}\right]$ (11)

获得3个以上靶球球心在机身坐标与激光坐标系下坐标，结合公式(1)利用最小二乘原理可解算出激光的外参数。在扫描仪静止状态下，移动靶球的位置来增加公共点数目作为多余观测，提高坐标系转换精度。

3. 实验与结果分析

本文采用仿真实验的方式，验证EPNP算法解算相机位置与姿态的鲁棒性。使用张正友棋盘格标定法进行相机内参数解算，求得公式(5)中提及的相机内参数，具体数值如表1所示 [13] 。

Table 1. Intrinsic parameters of camera

表1. 相机内参数

基于以上相机内参数，随机生成20组相互对应的三维点与二维点作坐标，在像素坐标真值的基础上加入白噪声后，进行位置与姿态参数解算，检验本算法标定结果鲁棒性。像素误差对相机姿态以及位置的解算精度的影响如图4所示。实验表明在像素误差低于2像素时，相机姿态解算误差低于0.001 rad，位置解算误差低于1 cm。重投影误差与原始像素误差关系如图4(c)所示，在多组仿真实验的计算中，其相关系数统计均高于0.9，即这两组数据间呈线性正相关关系。

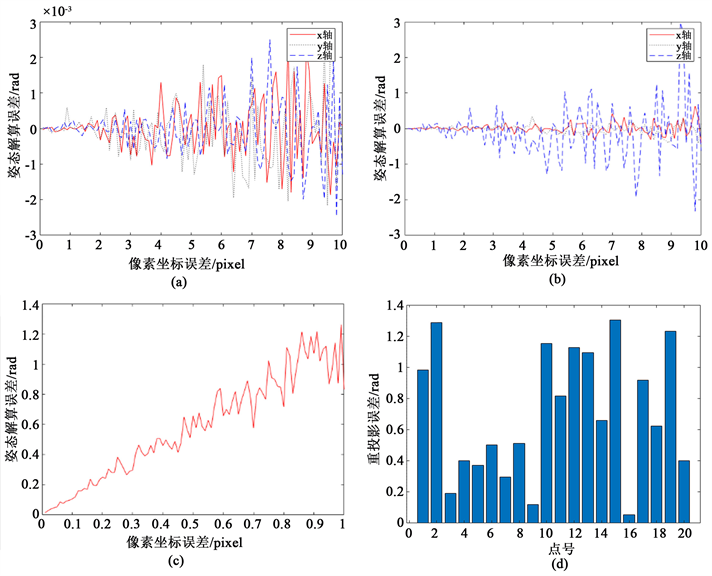
Figure 4. Experiment of camera extrinsic calibration, (a) Relationship between Pixel Error and Attitude solution accuracy; (b) Relationship between Pixel Error and Position solution accuracy; (c) Relationship between Pixel Error and Reprojection error; (d) Reprojection error of image control points

图4. 相机标定实验，(a) 像素误差与姿态解算精度的关系；(b) 像素误差与位置解算精度的关系；(c) 像素误差与重投影误差的关系；(d) 像控点的重投影误差

验证完相机位姿解算方法后正式展开标定实验，在相机有效视场内布置黑白靶标，作为相机外参数标定实验的控制点。使用Focus 3D X130型三维激光扫描仪获取标定场的三维点云数据，扫描点误差约为±2 mm。以机身控制点为中间转换点进行坐标转换，将标定场的扫描点云数据由独立坐标系转至机身坐标系，进而获取像控点在该坐标系下的三维坐标。从影像中提取像控点的像素坐标，建立三维点与二维像素间的对应关系。利用EPNP算法解算相机的外参数，得到6个外参数，基于求得的外参数将机身坐标系下坐标投影回像素坐标系，像控点的重投影误差如图4(d)所示，平均重投影误差约为0.7个像素。

在室内测图平台静止的情况下，对扫描仪进行外参数标定。标定实验中的靶球选用标准直径为145 mm的标准靶球。考虑到本实验选用的扫描仪解算出的单个点的点位精度为3 cm，采集100帧距离观测值取平均的方式降低距离观测误差，再根据角度信息进行解译，解译后点云如图5(a)所示。从解译好的点云中提取圆弧段，基于RANSAC方法进行圆拟合，噪点剔除后拟合结果如图5(b)所示。

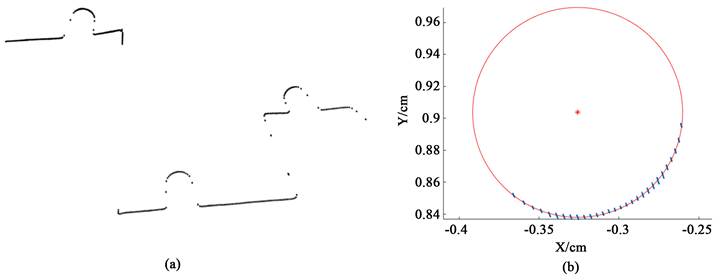
Figure 5. Experiment of 2D LiDAR extrinsic calibration, (a) Data interpretation of 2D LiDAR; (b) RANSAC circle fitting

图5. 二维扫描仪标定实验，(a) 扫描仪数据解译图；(b) 随机采样一致性圆拟合

三维扫描仪获取靶球表面点在机身坐标系下坐标，利用最小二乘法进行球拟合，获取靶球球心在机身坐标系下坐标。获取公共点在机身坐标转与激光坐标系下坐标，其对应关系如表2所示，基于共线方程求得激光坐标系与机身坐标系间坐标转换参数。理论上获取两个三维坐标系下3组公共点的坐标即可求得外参数，实际实验中为保证外参数解算的准确性，需获取多个公共点的坐标，使用4个公共点计算坐标转换参数，其余点作为检查控制点验证外参数精度。多次实验证明坐标系转换后，检查控制点点位残差小于1 cm。

Table 2. Coordinate of common points in 2D LiDAR extrinsic calibration experiment

表2. 二维扫描仪外参数标定实验中公共点坐标

至此，相机与扫描仪的标定均已经完成，得到6个标定外参数如表3所示。运用这些参数，可将相机与扫描仪等多种传感器的数据纳入到统一的机身坐标下。

Table 3. Experimental results of extrinsic calibration

表3. 传感器外参数标定结果

4. 总结与分析

本文实现了室内测图平台的多传感器外参数标定，建立机身坐标系，求取传感器坐标系与机身坐标系间的转换参数，借助该转换参数可将传感器纳入到统一的空间基准中。基于EPNP方法实现了相机外参数的解算，解算后点投影到相片中，像素误差低于1个像素；使用RANSAC圆拟合的方法实现了二维扫描仪的外参数标定，标定精度低于1个厘米。精度证明所涉及到的室内移动测图平台传感器标定方法能够满足实际工程的精度需求，对于搭载相机或扫描仪的机器人以及移动测量平台的传感器标定具有借鉴意义。未来将基于传感器联合标定结果，开展依赖于视觉和2D扫描仪的室内定位及建图研究。

基金项目

国家自然基金面上项目，项目编号：41771481。

NOTES

^*通讯作者。