1. 引言
目前,基于航空红外监测核电站温排水的方法正逐渐得到应用。2010年,江苏省辐射环境监测管理站对田湾核电站温排水进行监测,该实验在广泛调研的基础上,以航天遥感监测为主,航空监测为辅,船测、浮标监测为补充的方式,监测得到核电站温排水的影响状况,且空间分辨率达到了5 m~7.5 m,测温精度0.3℃,达到了环境监测的要求 [1] 。2016年中核集团三门核电有限公司根据实验验证载人飞机遥感监测的海温精度,在空间上分辨率精度达3 m~7.5 m、绝对温度精度为0.3℃、温升精度为0.1℃,可以在核电站附近海域进行海温监测 [2] 。2017年7月大连航天北斗科技有限公司进行了我国首例基于无人机航空遥感监测海水温度试验,该试验对辽宁红沿河核电站进行了温排水监测,分别监测了大潮高平、大潮低平、小潮高平、小潮低平四种状态下的海水温度,并制作了温升专题图,测温精度达到了0.3℃,试验证明,无人机红外遥感可以实时监测核电站温排水影响状况 [3] 。
无人机红外遥感监测核电站温排水具有远距离、速度快、非接触、灵敏度高、测温范围广等特点 [4] ,比传统的测温技术具有更大的优势,但也有诸多因素影响测温精度,如被测物体的辐射率、目标所处环境的辐射情况、目标所处环境温度、湿度、风速、光照强度等。此外,无人机红外成像仪在获取某些目标温度时,由于受无人机的飞行高度、横滚角、俯仰角、航向角、航速等姿态问题的影响,红外测温的精度也会受到影响。如何提高红外测温的精度是国内外学者重点关注的问题,例如张健等人研究了目标所处的环境温度对红外成像仪测温精度的影响 [5] ;官上洪等人主要研究了发射率、环境等效辐射、大气透过率、大气温度等因素对测温误差的影响,并推导出了测温精度的数学表达式 [6] 。上述红外成像仪测温误差校正与分析基本上是从原理着手,对于无人机搭载红外设备测温尚未进行过多的研究,从无人机飞行姿态及所处的环境条件等方面分析测温误差仅处于起步阶段,目前陈超帅等人通过无人机对目标温度进行监测,结合实测数据对测量结果进行了精度分析并给出误差源 [7] 。文献 [8] 将无人机获取的温度值采用小波神经网络进行拟合预测,拟合出的温度值精度在0.3℃以内。
本文在前人研究的基础上,从无人机飞行时的姿态角变化、各类气象参数比如环境气温、风速、空气湿度等对测温误差进行分析,采用机器学习的XGBoost进行仿真实验,预测得出的航拍温度值和实际温度值很接近,精度比采用BP神经网络与小波神经网络预测的温度值高,证明采用机器学习的XGBoost可以更精确的预测航拍温度;另外重点分析对测温误差影响较大的影响因素,如姿态角、风速、气温及湿度等,采用XGBoost理论对温度值进行预测,分析得出各个影响因素对航拍温度精度具有较大的影响,为后续试验时对测温精度的提高提供技术支撑。
2. XGBoost原理
2.1. XGBoost原理
近年来,陈天奇博士 [9] 对GBDT和AdaBoost算法进行了改进,提出一种高效、准确、灵活并且可移植性强的最优分布式决策梯度提升库(Extreme Gradient Boosting, XGBoost),它可以较为理想的解决预测问题,下面简要介绍XGBoost的基本理论。
在目前的试验以及应用当中,为了对某些数值预测,我们通常采用XGBoost有监督学习。有监督学习中,通常构造一个目标函数和一个预测函数,使用训练样本对目标函数最小化学习得到相关参数,然后用预测函数和训练样本得到的参数对未知的样本进行数值预测。目标函数Obj(θ)有两部分组成:误差函数L(θ)和复杂度函数Ω(θ)。学习的目标是尽量使损失偏差尽量小,函数尽量不复杂。
(1)
而XGBoost算法则用泰勒展开实现了更具有一般性的近似算法,且可以用代码实现,其目标函数:
(2)
其中,n表示样本含量,m表示第几次迭代,fm表示第m次迭代的误差,用泰勒公式展开:
 (3)
(3)
此时我们定义:
(4)
(5)
根据公式(5)可以看出XGBoost的目标函数只依赖于每个样本点在误差函数上的一阶导数和二阶导数。
2.2. XGBoost优势
无人机航拍数据具有变量多、数据量大等特点,XGBoost 算法是高效并行机器学习算法,适应多数据类型和多变量的情况,它借鉴了随机森林的算法,对样本、特征进行抽样,在降低过拟合的同时,减少计算量;与传统预测温度的方法相比,其能克服传统方法在数据规模较大情况下效率不够高的问题;同时,可以自定义损失函数,有规范化的正则项,使训练出的模型不易过拟合,有效利用无人机航拍的大规模数据提升温度预测精度。
3. 航拍试验
3.1. 测温实验
本次测温实验主要依托大连航天北斗科技有限公司,应用X80无人机对辽宁红沿河核电站温排水进行监测,获取夏季大、小潮4个潮态(涨急、涨末、落急、落末)各一次航空遥感测量海面温度场数据,同时结合海面温度监测,依据调查数据进行温度预测及测温误差分析。
3.2. 数据预处理
1) 数据筛选
无人机在飞行过程中,拐弯的地方有较大的晃动,将此部分数据剔除掉,根据重叠率要求选出可用POS点。POS数据含有时间信息,精确到秒;红外视频也含有时间信息,也精确到秒,按照已选POS数据的时间到红外视频文件中进行截帧,得到同时刻POS数据和带有温度信息的红外数据。
2) 确定空间分辨率
红外数据的分辨率为640 × 480,在镜头的视场范围内含有640 × 480个像元的温度值,像元投影到海面的真实大小与飞行高度成正比,1200 m高度飞机的视场角范围是1384.8 m × 988.8 m,空间分辨率即每个像元的大小2.2 m × 2.0 m。
3) 图像定位
将红外拍摄图像定位到正确的实际位置上需要的参数有:图像中心点坐标、拍摄高度、图像实际大小、航向角。图像的精确定位是测温正确性的前提。
4) 畸变校正
首先根据俯仰角、横滚角以及航高计算出图像中心点坐标投影到海面上的实际地理坐标,并进行几何畸变校正与桶形畸变校正;然后根据俯仰角度、横滚角度计算出图像投影到海面的实际长、宽;最后根据中心点坐标、边长、航向角度将图像对应的地理范围定位到正确的位置上。
5) 船测温度与航空温度对比提取
根据船测航线与无人机航线规划的重叠部分,提取船测温度与航拍温度在同一地点同一时间内的温度作为对比值。同步点的数量及正确率决定了本次验证温度的成功与否,故而,提取温度数量越多越好。
6) 气象参数的提取
结合辽宁省气象观测站,采集现场的温度、湿度、风速、风向、光照强度等。其中温度、湿度根据距海面的高度分为多个数值,如分为距离海面10米处的温度、湿度,20米处的温度、湿度等;风速同样按照高度进行采集,但是需将风速分为瞬时风速与平均风速,其余的气象参数均需详细采集。
3.3. 测温误差分析
根据提取的同步点温度值,对船测温度值和航拍红外温度值分析可知,两者存在某种对应的关系,个别数据由于定位误差和影像几何畸变未能完全校正而产生较大的误差,需要进行误差剔除,以确保温度校正的准确率。本文温度校正选择大潮高平时的同步点640个数数据,其中温差小于0.3℃的有554组,占比为86.56%。
4. XGBoost提高测温精度
4.1. XGBoost拟合温度实验
1) 特征选择
航拍温度与理想值之间存在误差,采用XGBoost对航拍温度进行拟合以期达到较为精准的结果。但是XGBoost拟合航拍温度需要考虑各类影响因素,主要包括无人机的航高、姿态角(航向角、横滚角、俯仰角)、环境温度、风速、湿度等,这些影响因素在XGBoost建模的过程中称之为特征,如表1所示。

Table 1. The main features of modeling
表1. 建模的主要特征
2) 温度预测流程
建模特征选取后,本文采用Python2.7上进行仿真实验,选取640组数据中的608组数据进行训练,32组数据作为测试集,采用XGBoost预测温度的过程如图1所示。

Figure 1. Flow chart of temperature prediction
图1. 温度预测流程图
3) 参数的优化
XGBoost模型存在大量可以调节的参数,例如eta、max_depth、nround、subsample、alpha、lambda、min_child_weight等;根据多次实验发现,XGBoost准确率虽然较高,但仍然有较高的提升空间,故而可以将参数逐个进行优化,每优化一个参数便可以提升一定的预测精度。
例如:gamma在树的叶子节点上进一步划分所需的最小损失减少,数值越大,算法越保守,默认0最为可靠。min_child_weight [default = 1]为叶子节点中最小的样本权重和,如果一个叶子节点的样本权重和小于min_child_weight则拆分过程结束,在现行回归模型中,这个参数是指建立每个模型所需要的最小样本数,典型值取1。max_delta_step这参数限制每棵树权重改变的最大步长,如果这个参数的值为0,那就意味着没有约束,如果它被赋予了某个正值,那么它会让这个算法更加保守,通常,这个参数不需要设置,但是本文航拍温度值的样本十分不平衡,为了得到更为接近逻辑回归,故而选择参数值0;subsample决定随机采样比例,减小这个参数的值,算法会更加保守,避免出现过拟合,但是,如果这个值设置得过小,它可能会导致欠拟合,本文经过多次试验得出参数值0.85最为符合理想要求。seed为随机数种子,用来生成可复制性的结果,本文数据选择1440组。scale_pos_weight在类别高度不平衡的情况下,将参数设置大于0,可以加快收敛。
根据多次实验,本次模型选择的重要参数如下:
max_depth = 5
learning_rate = 0.1
n_estimators = 75
silent = True
objective = 'reg:linear'
nthread = −1
gamma = 0
min_child_weight = 1
max_delta_step = 0
subsample = 0.85
colsample_bytree = 0.72
colsample_bylevel = 1
reg_alpha = 0
reg_lambda = 1
scale_pos_weight = 1
seed = 1440
4) 实验结果
按上述方法进行训练实验后,所测试的32组数据得到了较好的预测值,32组预测值中误差最大值为0.085℃,均方根误差为0.046,可知预测值精度基本满足要求,预测值、航拍值及原始值对比如图2所示。

Figure 2. Temperature fitting comparison chart
图2. 温度拟合对比图
神经网络同样可以很好的预测温度值,如文献 [8] 采用小波神经网络对航拍温度数据进行拟合,同样的采用BP神经网络对航拍温度进行预测,预测的32组温度值误差对比图如图3所示。
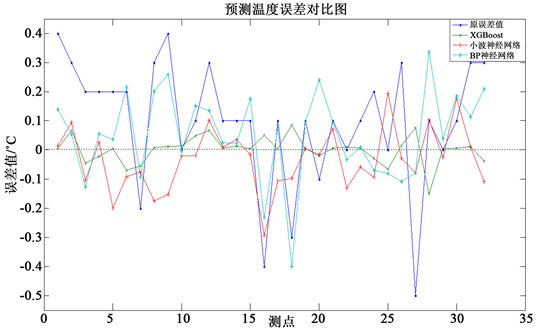
Figure 3. Temperature fitting comparison chart
图3. 预测温度误差值对比图
根据三者的预测结果进行精度评价,如表2所示:XGBoost预测的温度精度值最高,其次是小波神经网络拟合的温度值,均方根误差约为0.1左右,预测温度误差最大值为0.177℃;而BP神经网络预测的温度值相比较另外两种方法预测的温度精度最低,造成小波神经网络与BP神经网络拟合精度低于XGBoost拟合精度的主要原因是两者均未考虑诸项外在的影响因素对测温误差的影响,所以各类影响因素是不可忽略的。

Table 2. Comparison and analysis table of prediction temperature accuracy
表2. 预测温度精度对比分析表
4.2. 测温误差分析
考虑上述影响航拍温度的因素后,采用XGBoost预测出的温度值较为理想,基本确定上述各种影响因素对航拍温度的确造成了不可忽略的影响,但是并不能确定每种影响因素对航拍温度精度的影响程度,为此,采用4.1节的方法,在Python2.7进行仿真实验,分析重要的影响因素对航拍温度造成的误差,为后续的相关实验进行误差排除。
4.2.1. 影响因素重要度分析
航拍温度影响因素较多,为了分析每种影响因素对温度误差的影响程度,本文在4.1节预测值的基础上分析每种因素的重要性,采用Python进行仿真实验,关键程序如下:
plot_importance(xgb_boost, importance_type = 'weight')
pyplot.show()
print(xgb_boost.feature_importances_)
实验分析结果如图4所示。实验表明,航拍温度影响度最大,因为航拍温度本身就是误差修正的主要特征;其次影响度为0.0517的10米高度处的瞬时风速值;然后是POS数据的影响,如横滚角、俯仰角、航高等,其中航高在姿态角中对温度的影响最大,达到了0.0463;影响度较小的为30米高度处的最大风速、10米高度处的空气湿度、GPS、80米和100米高度处2分钟内的风速、以及10米高度处的空气温度等。从大类影响因素来说,当时环境的风速、温度、湿度依然影响最大,这些影响因素在反演温度时虽然已经被国内外的学者进行了充分的研究,但是从XGBoost上来说还未进行过研究,所以重点关注对航拍温度影响度较大的因素,如各类姿态角、航高、风速、温度、湿度等,将这些影响因素逐一进行考虑分析,验证误差是否随着影响因素的增多而逐渐减小。
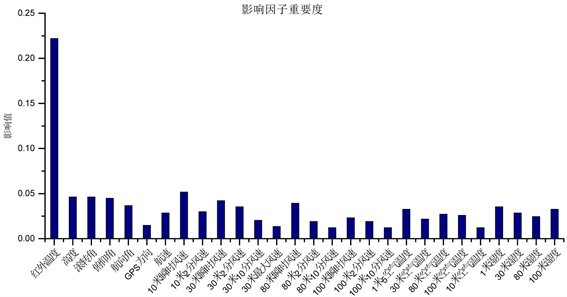
Figure 4. Importance of influencing factors
图4. 影响因素重要度
4.2.2. 姿态角的影响
无人机在飞行的过程中由于飞控系统的误差以及气流的影响,无人机的姿态时刻处于变化状态,内业处理时虽已对影片进行了几何校正,但是并不能完全校正姿态角造成的实际成像误差,致使所测目标值与实际值不符合;另外姿态角是一组不可分割的数据组,不可单独的分析对测温误差影响的程度,需要综合性的考虑。本文为了验证姿态角对测温精度的影响值,在无人机的航向角、横滚角、俯仰角、航高、航速等因素作用下通过XGBoost进行温度预测,并将预测值与船测值进行对比分析。采用上述640数据进行实验,预测出的32对温度的误差如图5所示。
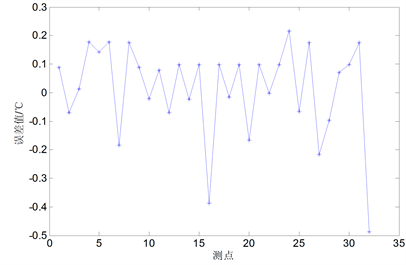
Figure 5. Temperature prediction error graph
图5. 预测温度误差图
本次实验预测温度误差最大值为0.387℃,均方根误差为0.180,未进行温度校正前的船测温度与航拍温度最大误差为0.5℃,均方根误差为0.231,从以上结果对比可知,无人机的姿态角是影响航拍温度值不可或缺的重要因素。故而为了得到更高精度的航拍温度值,必须将无人机的姿态角因素考虑在内。
4.2.3. 风速的影响
由于被测物体在室外,环境温度和目标温度会受风速的影响。当风速很大时,会造成向外散热,目标的热量被风力加速吹散,则相对应的目标景物下降,致使所测温度比实际温度低。比如风速为1 m/s,某电线设备接头的温度是60℃,根据经验公式换算,在风速为4 m/s时,该设备接头的温度仅为30℃,所以风速对误差影响不可忽视。
本次航测实验采用红沿河核电站气象观测站观测的数据资料,与航拍同步观测,这样减少了时间上不同步造成的误差问题。本次的风速因子包含有10米高度处的平均风速与瞬时风速、30米高度处的平均风速与瞬时风速、80米高度处的平均风速与瞬时风速、100米高度处平均风速与瞬时风速,为了分析风速对航拍值的影响,将各类风速因素均考虑在内,温度预测结果误差如图6所示:
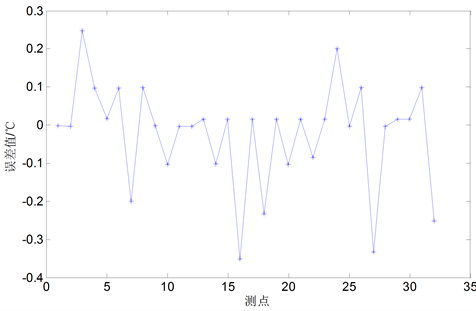
Figure 6. Temperature prediction error graph
图6. 预测温度误差图
预测的结果显示,本次预测温度的最大误差为0.351℃,均方根误差为0.144,与4.2.2节考虑姿态角对航拍温度值的影响相比,最大误差值已经减小,均方根误差也有所减小。
4.2.4. 湿度、气温的影响
1) 气温与湿度共同影响
根据大量的实验表明,当背景温度介于(T − 10)~(T + 25)之间时,红外测量的精度较高。在进行红外测温实验之前已经对红外成像仪影响进行了标定试验,对室外温度的影响已经进行了温度补偿。但是环境中的气温时刻在变化,比如本次测量过程中不同高度处的气温值不同,且随时间也在发生变化,这对监测温度产生了一定的影响。另外,当大气湿度大于85%的情况时,由于水蒸汽密度增加,增大了对红外辐射吸收,大气对目标物体辐射的衰减急剧加大,因此,在雨雾天气下不适宜进行红外监测;但是大气的湿度低于85%时,红外测温依然会受影响,所以综合气温和湿度这两个影响因素,探讨两者对红外测温的精度影响的程度,并分析两者对温度影响的占比情况。
实验时将不同高处的气温与大气湿度考虑进影响测温的行列,实验结果如图7所示。
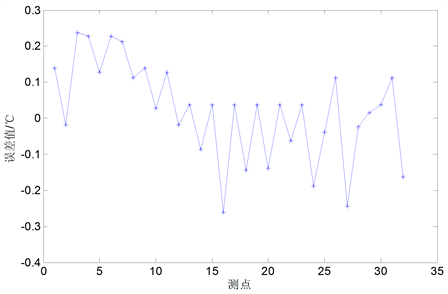
Figure 7. Temperature prediction error graph
图7. 预测温度误差图
实验结果显示,当考虑气温与湿度的共同影响后,预测温度最大误差为0.262℃,均方根误差为0.134,误差值再次减小。
1) 气温、湿度单独作用下的影响
在气温与湿度的共同作用下,预测的温度值精度比未进行校正前的温度值有了较大的提升,可见气温与湿度是影响测温误差的重要因素。为了探讨两者对气温的影响大小,将两个因素分别进行验证其对预测温度值的影响,首先进行在仅有气温因素作用下对航拍值进行预测值,其次进行仅有湿度作用下航拍值的预测。
实验的结果显示,当仅有气温参与温度预测时,预测温度误差的最大值为0.315℃,均方根误差为0.179;当仅有湿度参与温度预测时,预测温度误差最大值为0.316℃,均方根误差为0.144。通过对比分析,湿度对红外测温精度的影响比气温的影响大,这也比较符合原理上的解释,湿度较大时,空气中悬浮过多的水滴,将影响海面的辐射波,造成一定的折射或者漫反射,故而对测温影响较为显著。图8为气温、湿度、气温与湿度的测温误差对比曲线图。

Figure 8. Temperature and humidity temperature error comparison chart
图8. 气温、湿度测温误差对比图
2) 气温、湿度影响误差分析
根据仿真实验结果可知,将气温与湿度影响因素单独进行温度预测,其精度均低于将气温与湿度共同作用下预测温度的精度值,可以得出气温和湿度是影响测温误差因素的重要组合部分。
5. 结束语
采用机器学习中的XGBoost进行温度的拟合,并将各类影响航拍温度的因素考虑在内,预测出的温度值很符合理想值(船测值),证明本方法在航拍温度的校正中可以很好的应用。
分析影响航拍温度精度的影响因素,并对各个影响因素进行重要度检验,检验结果很好地展示出各个影响因素的重要程度。结合本次航拍试验出现的航高、姿态角、风速、气温、湿度等影响误差的因素,利用XGBoost的原理进行温度值预测,重点分析重要度较大的影响因素对测温精度的影响,判断得出姿态角、风速、气温及湿度对航拍温度造成的误差较大,在进行航拍测温试验时需要重点将这些因素考虑在内,以便于预测得到更高精度的温度值。
基金项目
国家自然科学基金项目资助(批准号:51778111)。
NOTES
*通讯作者。