具有全状态时变约束非线性不确定电机系统的自适应容错控制

Adaptive Fault-Tolerant Control for Nonlinear Uncertain Electromechanical Systems with Full-State Time-Varying Constraints

摘要: 本文针对具有全状态时变约束的非线性电机系统，提出了自适应神经网络容错控制策略。为了保证系统控制性能，构建了容错补偿控制器消除执行器失效故障和偏移故障的影响。引入时变障碍李雅普诺夫函数，保证全部系统状态不超出指定时变约束范围，尤其是在执行器发生故障情况下也未违反状态约束限制。利用神经网络作为逼近器处理系统中未知函数。基于李雅普诺夫稳定性分析，证明了闭环系统中全部信号的有界性，以及系统输出良好的跟踪性能。仿真结果进一步说明所提出控制策略的有效性。

Abstract: This paper proposes an adaptive fault-tolerant control method for nonlinear electromechanical system with full-state time varying constraints. In order to ensure the control performance of the system, a fault tolerant compensation controller is constructed to eliminate the influence of the actuator loss of effectiveness and bias fault. The time-varying barrier Lyapunov functions are in-troduced to ensure that all the system state does not exceed the specified time-varying constraint range; especially in the case of actuator failure, the full-state constraints are not violated. Neural network as the approximator is employed to approximate unknown function in the processing system. Based on the Lyapunov analysis, it is proved that all the signals in the closed-loop system are bounded and the good tracking performance of the system is achieved. The simulation results further illustrate the effectiveness of the proposed control strategy.

1. 引言

由于现代工程系统趋向于规模化、复杂化，并伴随着高度非线性和不确定性等特点，此类系统通常无法建立精确的数学模型。因此，经典自适应控制方法难以对此类系统进行有效地控制。基于神经网络和模糊逻辑系统的自适应控制方法受到了越来越多的关注。针对具有未知状态时滞和输入时滞的非线性系统，文 [1] [2] 分别提出了自适应模糊和神经网络控制算法，有效地消除了时滞对系统性能的影响。文 [3] 设计了自适应模糊控制器，解决了具有未知死区的非线性多输入多输出系统的跟踪控制问题。考虑控制增益信号未知的情况，文 [4] 结合Nussbaum增益和动态面技术，不仅克服了控制信号未知问题，还避免了返步法中出现的计算爆炸问题。上述这些防止方法均要求系统状态已知，然而由于工作环境影响和测量成本过高等因素，系统状态往往是未知的。为了克服上述控制方法的弊端，文 [5] 研究具有非光滑输入的非线性系统，提出了自适应输出反馈控制。这些控制方法都是在执行器无故障的情况下提出的。

执行器作为执行终端往往工作在高温高压和腐蚀性等恶劣环境，发生各种故障情况是不可避免的。为此，许多学者致力于研究具有执行器故障的非线性系统问题。针对一类严格反馈开关非线性系统，在 [6] 中提出了自适应神经网络有限时间容错控制方法。作为文 [6] 所提出的方法的拓展，文 [7] [8] 分别针对具有执行器故障的MIMO系统和随机系统，提出了稳定的自适应容错跟踪控制。文 [9] 提出了一种自适应容错控制策略，并将其应用于近空间飞行器。这些控制方法都是针对状态可测的非线性系统提出。采用自适应反步方法，文 [10] 针对状态不可测的大型非线性系统，设计了自适应模糊容错控制器。然而，这些容错控制方法都是针对无约束系统所提出的。

由于操作空间、安全因素以及各种性能指标限制，系统状态需被约束在一定的范围内，一旦约束限制被违反，势必造成系统控制性能损失。文 [11] 首次提出了基于障碍李雅普诺夫函数的自适应控制方法，解决了非线性单输入单输出系统的输出约束控制问题。文 [12] 进一步解决了部分状态约束问题。文 [11] [12] 的主要局限在于被控系统中非线性函数必须为已知，或满足线性参数化。基于神经网络和模糊逻辑系统的逼近能力，文 [13] [14] 分别提出了稳定的自适应控制方法分别保证了常数输出约束和常数状态约束未被违反。常数约束仅为时变约束的特例，时变约束更加符合实际工程系统的需求。针对严格反馈系统 [15] 、纯反馈系统 [16] 、随机系统 [17] 和大系统 [18] ，学者们提出了大量的自适应时变约束控制方法。此外，基于障碍李雅普诺夫函数的自适应控制方法也广泛地应用于各种工程系统，如机器人系统 [19] 、电机系统 [20] 、龙门起重机系统 [21] 和连续搅拌釜系统 [22] 。

本文针对具有全状态时变约束的电机系统，基于时变障碍李亚普诺夫函数提出了自适应神经网络控制方法。利用神经网络对系统中未知函数进行逼近。通过稳定分析，证明了闭环系统中信号都是有界的，跟踪误差收敛至原点小的邻域内。本文的主要贡献点总结如下：1) 针对电机系统，同时考虑了全状态时变约束和执行器故障，提高了应用的范围。2) 考虑了执行器失效故障和偏移故障，提出故障补偿器消除故障对系统的影响。3) 通过构建新型时变障碍李雅普诺夫函数，保证全状态时变约束不被违反。最后，给出仿真例子说明了所提出方法的有效性。

2. 问题描述及预备知识

考虑如下电机系统动力学方程

$\{\begin{array}{l}\left(\frac{J}{K_{\tau }}+\frac{M_0{L}_0^2}{3K_{\tau }}+\frac{2M_0{R}_0^2}{5K_{\tau }}\right)\ddot{q}+\left(\frac{B_0}{K_{\tau }}\right)\stackrel{\dot{}}{q}+\left(\frac{m{L}_{0}G}{2K_{\tau }}+\frac{M_0{L}_{0}G}{K_{\tau }}\right)\sin \left(q\right)=I\\ L\stackrel{\dot{}}{I}=\tau -RI-K_B\stackrel{\dot{}}{q}\end{array}$ (1)

其中，J是转子惯性， $M_0$ 表示负载质量， $L_0$ 是连杆长度，m未知连杆质量， $R_0$ 是负载半径，G代表重力系数， $B_0$ 是未知关节处的粘性摩擦系数， $q\left(t\right)$ 为角电机位置， $I\left(t\right)$ 是电机的电流， $K_{\tau }$ 表示转矩系数。L是电枢电感，R是电枢电阻， $K_B$ 是未知反电势系数， $\tau$ 是输入控制电压。

定义 $x_1=q$ ， $x_1=\stackrel{\dot{}}{q}$ 和 $x_3=I$ ，以及 $M=J/K_{\tau }+M_0{L}_0^2/3K_{\tau }+2M_0{R}_0^2/5K_{\tau }$ ， $N=m{L}_{0}G/2K_{\tau }+M_0{L}_{0}G/K_{\tau }$ ， $B=B_0/K_{\tau }$ ，动力学方程(1)可以被重写为

$\{\begin{array}{l}{\stackrel{\dot{}}{x}}_1=x_2\\ {\stackrel{\dot{}}{x}}_2=\frac{1}{M}{x}_3-\frac{N}{M}\sin \left(x_1\right)-\frac{B}{M}{x}_2\\ {\stackrel{\dot{}}{x}}_3=\frac{1}{L}\tau -\frac{K_B}{L}{x}_2-\frac{R}{L}{x}_3\\ y=x_1\end{array}$ (2)

为了保证控制品质和系统平稳运行，系统状态需要满足如下的约束条件：

$\left|x_i\right|\le {\psi }_i\left(t\right),i=1,2,3$ (3)

其中， ${\lambda }_i$ 为用户设定的参数。

本文的主要控制目标：设计稳定的自适应输出反馈约束控制方法来保证：

1) 闭环系统中所有信号有界；

2) 跟踪误差和估计误差尽可能小；

3) 系统状态不超出指定的约束范围。

在本文中，为了提高执行机构失效时的瞬态调节性能，构建容错控制器如下：

$\tau =lu+\zeta ,\forall t\ge T$ (4)

其中，u表示致动器的控制输入，l表示失效百分数，以及 $\zeta$ 为偏移故障，T表示执行器发生故障的时间。

失效故障和偏移故障的具体说明如下

失效故障： $0<l\le 1$ 且 $\zeta =0$ ，容错控制器 $\tau =lu$

若 $l=1$ ，执行器没有任何失效。例如 $l=0.8$ ，执行器效率失效20%。

偏移故障： $\zeta \ne 0$ 且 $l=0$ ，容错控制器 $\tau =\zeta$

执行器不再随着控制信号变化而改变。

注释1：尽管针对具有约束的实际系统，文 [19] [20] [21] [22] 提出一些自适应控制方法很好地保证系统的稳定性。但是这些研究成果都是针对系统正常运行情况下提出的，本文能够保证电机系统正常运行时还是执行器发生故障情况下，系统状态始终满足时变约束条件。

假设1：存在正常数 $K_i,i=1,2,3$ ，满足 $\left|{\psi }_i\left(t\right)\right|\le K_i^0$ ，且 ${\psi }_i\left(t\right)$ 的第j次导数满足 $\left|y_r^{\left(j\right)}\right|\le K_i^{\left(j\right)},j=1,2,3$ 。

假设2：假设存在正函数 $A\left(t\right)$ 和正常数 $B_i,i=1,2,3$ ，这样期望轨迹 $y_r$ 和其导数满足 $\left|y_r\left(t\right)\right|\le A\left(t\right)<{\psi }_1\left(t\right)$ 和 $\left|y_r^{\left(i\right)}\left(t\right)\right|\le B_i$ 。

假设3：存在已知正常数 $\underset{\_}{l}$ 和 $\bar{\zeta }$ ，满足 $\underset{\_}{l}\le l\le 1$ 和 $\left|\zeta \right|\le \bar{\zeta }$ 。

注释2：假设1是用来说明系统状态的约束界及其导数都是有界的。假设2显示期望跟踪信号是有界的，并且上界不超过系统输出的约束范围，以及跟踪信号导数有界性。假设3指出执行器失效故障存在下界，偏移故障存在上界。假设1和2普遍存在于现有自适应时变约束控制文献 [18] [20] 。假设3是较为温和的，容错控制文献 [8] [9] [10] 经常给出此假设。

3. 自适应神经网络控制器设计及稳定性分析

在本节中，为了保证电机系统运行过程的暂态和瞬态不超出指定的约束范围，尤其是在故障发生以后，自适应神经网络控制器详细设计过程如下。

步骤1：定义误差变量 $e_1=x_1-y_r$ ，其导数可以表示为

${\stackrel{\dot{}}{e}}_1={\stackrel{\dot{}}{x}}_1-{\stackrel{\dot{}}{y}}_d=e_2+{\chi }_1-{\stackrel{\dot{}}{y}}_r$ (5)

其中，误差变量 $e_2=x_2-{\chi }_1$ ，虚拟控制器 ${\chi }_1$ 的定义将稍后给出。

选取障碍李雅普诺夫函数

$V_1=\frac{{\lambda }_1^2}{\text{π}}\tan \left(\frac{\text{π}{e}_1^2}{2{\lambda }_1^2}\right)$ (6)

考虑(5)，(6)的导数为

${\stackrel{\dot{}}{V}}_1=\frac{2{\lambda }_1{\stackrel{\dot{}}{\lambda }}_1}{\text{π}}tan\left(\frac{\text{π}{e}_1^2}{2{\lambda }_1^2}\right)+{\sec }^2\left(\frac{\text{π}{e}_1^2}{2{\lambda }_1^2}\right)e_1{e}_2-\frac{e_1^2{\stackrel{\dot{}}{\lambda }}_1}{{\lambda }_1}{\sec }^2\left(\frac{\text{π}{e}_1^2}{2{\lambda }_1^2}\right)+{\sec }^2\left(\frac{\text{π}{e}_1^2}{2{\lambda }_1^2}\right)e_1\left({\chi }_1-{\stackrel{\dot{}}{y}}_r\right)$ (7)

构建虚拟控制器如下

${\chi }_1=-\left({\rho }_1+2{\bar{\lambda }}_1\right)\frac{{\lambda }_1^2}{2\text{π}{e}_1}\sin \left(\frac{\text{π}{e}_1^2}{{\lambda }_1^2}\right)-e_1{\bar{\lambda }}_1+{\stackrel{\dot{}}{y}}_r$ (8)

其中， ${\bar{\lambda }}_i=\sqrt{{\left({\stackrel{\dot{}}{\lambda }}_i/{\lambda }_i\right)}^2+{\gamma }_i}$ ， ${\gamma }_1>0$ 为已知常数。因此，可以得到 ${\bar{\lambda }}_i+{\stackrel{\dot{}}{\lambda }}_i/{\lambda }_i>0$ 和 ${\bar{\lambda }}_i-{\stackrel{\dot{}}{\lambda }}_i/{\lambda }_i>0$ 。

注释3：根据洛必达法则可得

$\underset{e\to 0}{\lim }\frac{{\lambda }_1^2}{2\text{π}{e}_1}\sin \left(\frac{\text{π}{e}_1^2}{{\lambda }_1^2}\right)=0$

因此，虚拟控制器 ${\chi }_1$ 中不存在奇点。

结合(7)和(8)，我们可以得到

${\stackrel{\dot{}}{V}}_1=-\frac{{\rho }_1{\lambda }_1^2}{\text{π}}\tan \left(\frac{\text{π}{e}_1^2}{2{\lambda }_1^2}\right)+{\sec }^2\left(\frac{\text{π}{e}_1^2}{2{\lambda }_1^2}\right)e_1{e}_2$ (9)

其中，由 ${\bar{\lambda }}_1$ 的定义可知 $\frac{2{\lambda }_1^2}{\text{π}}\tan \left(\frac{\text{π}{e}_1^2}{2{\lambda }_1^2}\right)\left(\frac{{\stackrel{\dot{}}{\lambda }}_1}{{\lambda }_1}-{\bar{\lambda }}_1\right)<0$ 且 $-e_1^2{\sec }^2\left(\frac{\text{π}{e}_1^2}{2{\lambda }_1^2}\right)\left(\frac{{\stackrel{\dot{}}{\lambda }}_1}{{\lambda }_1}+{\bar{\lambda }}_1\right)<0$ 。

步骤2：根据(2)和定义 $e_2=x_2-{\chi }_1$ ，误差变量 $e_2$ 的导数可表示为

${\stackrel{\dot{}}{e}}_2={\stackrel{\dot{}}{x}}_2-{\stackrel{\dot{}}{\chi }}_1=\frac{1}{M}{x}_3-\frac{N}{M}\sin \left(x_1\right)-\frac{B}{M}{x}_2-{\stackrel{\dot{}}{\chi }}_1$ (10)

其中， ${\stackrel{\dot{}}{\chi }}_1=\frac{\partial {\chi }_1}{\partial x_1}{x}_2+{\displaystyle {\sum }_{j=0}^1\frac{\partial {\chi }_1}{\partial y_r^{\left(j\right)}}{y}_r^{\left(j+1\right)}}$ 。

选取障碍李雅普诺夫函数如下

$V_2=\frac{{\lambda }_2^2}{\text{π}}\tan \left(\frac{\text{π}{e}_2^2}{2{\lambda }_2^2}\right)+\frac{1}{2}{\tilde{\Theta }}_1^2+V_1$ (11)

其中， ${\tilde{\Theta }}_1={\hat{\Theta }}_1-{\Theta }_1^{\ast }$ ， ${\hat{\Theta }}_1$ 是最优权重向量 ${\Theta }_1^{\ast }$ 的估计权重。

因此， $V_2$ 导数可得

$\begin{array}{c}{\stackrel{\dot{}}{V}}_2=\frac{2{\lambda }_2{\stackrel{\dot{}}{\lambda }}_2}{\text{π}}tan\left(\frac{\text{π}{e}_2^2}{2{\lambda }_2^2}\right)-\frac{e_2^2{\stackrel{\dot{}}{\lambda }}_2}{{\lambda }_2}{\sec }^2\left(\frac{\text{π}{e}_2^2}{2{\lambda }_2^2}\right)+\frac{1}{M}{\sec }^2\left(\frac{\text{π}{e}_2^2}{2{\lambda }_2^2}\right)e_2{e}_3\\ +\frac{1}{M}{\sec }^2\left(\frac{\text{π}{e}_2^2}{2{\lambda }_2^2}\right)e_2{\chi }_2+{\sec }^2\left(\frac{\text{π}{e}_2^2}{2{\lambda }_2^2}\right)e_2{F}_1\left(Z_1\right)+{\tilde{\Theta }}_1{\stackrel{\dot{}}{\hat{\Theta }}}_1+{\stackrel{\dot{}}{V}}_1\end{array}$ (12)

其中， $Z_1={\left[x_1,x_2,y_r,{\stackrel{\dot{}}{y}}_r\right]}^{\text{T}}$ ，定义未知函数 $F_1\left(Z_1\right)=\sin \left(x_1\right)N/M+x_{2}B/M+{\stackrel{\dot{}}{\chi }}_1$ 。

将RBFNNs作为函数逼近器对未知函数 $F_1\left(Z_1\right)$ 进行逼近

$F_1\left(Z_1\right)=W_1^{\ast \text{T}}{S}_1\left(Z_1\right)+{\epsilon }_1\left(Z_1\right)$ (13)

其中， ${\tilde{W}}_1={\hat{W}}_1-W_1^{\ast }$ 是权重估计误差，估计权重向量 ${\hat{W}}_1$ 用来估计未知最优权重向量 $W_1^{\ast }$ 。存在正常数 ${\bar{\epsilon }}_1$ 和 ${\bar{W}}_1$ ，使得不等式 $\left|{\epsilon }_1\left(Z_1\right)\right|\le {\bar{\epsilon }}_1$ 和 $\left|W_1^{\ast }\right|\le {\bar{W}}_1$ 成立。

结合(13)和(12)并利用杨氏不等式，可得

${\sec }^2\left(\frac{\text{π}{e}_2^2}{2{\lambda }_2^2}\right)e_2{W}_1^{\ast \text{T}}{S}_1\left(Z_1\right)\le \frac{1}{2{\sigma }_1^2}{\sec }^4\left(\frac{\text{π}{e}_2^2}{2{\lambda }_2^2}\right)e_2^2{\bar{W}}_1^2{\Vert S_1\left(Z_1\right)\Vert }^2+\frac{{\sigma }_1^2}{2}$ (14)

${\sec }^2\left(\frac{\text{π}{e}_2^2}{2{\lambda }_2^2}\right)e_2{\epsilon }_1\left(Z_1\right)\le \frac{1}{2}{\upsilon }_1{e}_2^2{\sec }^4\left(\frac{\text{π}{e}_2^2}{2{\lambda }_2^2}\right)+\frac{{\bar{\epsilon }}_1^2}{2{\upsilon }_1}$ (15)

其中， ${\sigma }_1$ 和 ${\upsilon }_1$ 是正设计参数。定义 ${\Theta }_i^{\ast }={\bar{W}}_i^2,i=1,2$ 。

设计虚拟控制器和自适应率如下

$\begin{array}{c}{\chi }_2=-M[\left({\rho }_2+2{\bar{\lambda }}_2\right)\frac{{\lambda }_2^2}{2\text{π}{e}_2}\sin \left(\frac{\text{π}{e}_2^2}{{\lambda }_2^2}\right)+e_2{\bar{\lambda }}_2+\frac{{\upsilon }_1}{2}{e}_2{\sec }^2\left(\frac{\text{π}{e}_2^2}{2{\lambda }_2^2}\right)\\ +\frac{1}{2{\sigma }_1^2}{\sec }^2\left(\frac{\text{π}{e}_2^2}{2{\lambda }_2^2}\right)e_2{\hat{\Theta }}_1{\Vert S_1\left(Z_1\right)\Vert }^2+{\sec }^2\left(\frac{\text{π}{e}_1^2}{2{\lambda }_1^2}\right){\cos }^2\left(\frac{\text{π}{e}_2^2}{2{\lambda }_2^2}\right)e_1]\end{array}$ (16)

${\stackrel{\dot{}}{\hat{\Theta }}}_1=\frac{1}{2{\sigma }_1^2}{\sec }^4\left(\frac{\text{π}{e}_2^2}{2{\lambda }_2^2}\right)e_2^2{\Vert S_1\left(Z_1\right)\Vert }^2-{\gamma }_1{\hat{\Theta }}_1$ (17)

其中， ${\gamma }_1$ 是正常数。

注释4：利用未知神经权重向量的范数作为估计参数，这大大减少了神经网络输入变量的数量，减轻了计算负担。

将(9)，(14)~(17)代入(12)可得到如下不等式

${\stackrel{\dot{}}{V}}_2=-{\displaystyle \underset{j=1}{\overset{2}{\sum }}\frac{{\rho }_j{\lambda }_j^2}{\text{π}}\tan \left(\frac{\text{π}{e}_j^2}{{\lambda }_j^2}\right)}-{\gamma }_1{\tilde{\Theta }}_1{\hat{\Theta }}_1+\frac{1}{M}{\sec }^2\left(\frac{\text{π}{e}_2^2}{2{\lambda }_2^2}\right)e_2{e}_3+\frac{{\bar{\epsilon }}_1^2}{2{\upsilon }_1}+\frac{{\sigma }_1^2}{2}$ (18)

步骤3：定义误差向量 $e_3=x_3-{\chi }_2$ 。结合(2)和(4)， $e_3$ 导数表示为

${\stackrel{\dot{}}{e}}_3={\stackrel{\dot{}}{x}}_3-{\stackrel{\dot{}}{\chi }}_2=\frac{1}{L}\left(lu+\zeta \right)-\frac{K_B}{L}{x}_2-\frac{R}{L}{x}_3-{\stackrel{\dot{}}{\chi }}_2$ (19)

其中， ${\stackrel{\dot{}}{\chi }}_2={\displaystyle {\sum }_{j=1}^2\frac{\partial {\chi }_j}{\partial x_j}{\stackrel{\dot{}}{x}}_j}+{\displaystyle {\sum }_{j=0}^2\frac{\partial {\chi }_1}{\partial y_r^{\left(j\right)}}{y}_r^{\left(j+1\right)}}+{\displaystyle {\sum }_{j=1}^2\frac{\partial {\chi }_j}{\partial {\hat{\Theta }}_j}{\stackrel{\dot{}}{\hat{\Theta }}}_j}$ 。

选取障碍李雅普诺夫函数如下

$V_3=\frac{{\lambda }_3^2}{\text{π}}\tan \left(\frac{\text{π}{e}_3^2}{2{\lambda }_3^2}\right)+\frac{1}{2}{\tilde{\Theta }}_2^2+V_2$ (20)

其求导可得

$\begin{array}{c}{\stackrel{\dot{}}{V}}_3\le \frac{2{\lambda }_3{\stackrel{\dot{}}{\lambda }}_3}{\text{π}}tan\left(\frac{\text{π}{e}_3^2}{2{\lambda }_3^2}\right)-\frac{e_3^2{\stackrel{\dot{}}{\lambda }}_3}{{\lambda }_3}{\sec }^2\left(\frac{\text{π}{e}_3^2}{2{\lambda }_3^2}\right)+{\tilde{\Theta }}_2{\stackrel{\dot{}}{\hat{\Theta }}}_2+{\stackrel{\dot{}}{V}}_2\\ +\frac{1}{L}{\sec }^2\left(\frac{\text{π}{e}_3^2}{2{\lambda }_3^2}\right)e_3\left(lu\right)-{\sec }^2\left(\frac{\text{π}{e}_3^2}{2{\lambda }_3^2}\right)e_3{F}_2\left(Z_2\right)\end{array}$ (21)

其中， $F_2\left(Z_2\right)=x_2{K}_B/L+x_{3}R/L+{\stackrel{\dot{}}{\chi }}_2-\zeta /L$ 。

利用神经网络对未知函数 $F_2\left(Z_2\right)$ 进行逼近

$F_2\left(Z_2\right)=W_2^{\ast \text{T}}{S}_2\left(Z_2\right)+{\epsilon }_2\left(Z_2\right)$ (22)

其中， ${\tilde{W}}_2={\hat{W}}_2-W_2^{\ast }$ 是权重估计误差，估计权重向量 ${\hat{W}}_2$ 用来估计未知最优权重向量 $W_2^{\ast }$ 。存在正常数 ${\bar{\epsilon }}_2$ 和 ${\bar{W}}_2$ ，使得不等式 $\left|{\epsilon }_2\left(Z_2\right)\right|\le {\bar{\epsilon }}_2$ 和 $\left|W_2^{\ast }\right|\le {\bar{W}}_2$ 成立。

利用杨氏不等式，我们可以得到

$-{\sec }^2\left(\frac{\text{π}{e}_3^2}{2{\lambda }_3^2}\right)e_3{W}_2^{\ast \text{T}}{S}_2\left(Z_2\right)\le \frac{1}{2{\sigma }_2^2}{\sec }^4\left(\frac{\pi e_2^2}{2{\lambda }_2^2}\right)e_3^2{\bar{W}}_2^2{\Vert S_2\left(Z_2\right)\Vert }^2+\frac{{\sigma }_2^2}{2}$ (23)

$-{\sec }^2\left(\frac{\text{π}{e}_3^2}{2{\lambda }_3^2}\right)e_3{\epsilon }_2\left(Z_2\right)\le \frac{1}{2}{\upsilon }_2{e}_3^2{\sec }^4\left(\frac{\text{π}{e}_3^2}{2{\lambda }_3^2}\right)+\frac{{\bar{\epsilon }}_2^2}{2{\upsilon }_2}$ (24)

其中， ${\sigma }_2$ 和 ${\upsilon }_2$ 是正设计参数。

设计控制输入和自适应率如下

$\begin{array}{c}u=-\frac{L}{l}[\left({\rho }_3+2{\bar{\lambda }}_3\right)\frac{{\lambda }_3^2}{2\text{π}{e}_3}\sin \left(\frac{\text{π}{e}_3^2}{{\lambda }_3^2}\right)+e_3{\bar{\lambda }}_3+\frac{{\upsilon }_2}{2}{e}_3{\sec }^2\left(\frac{\text{π}{e}_3^2}{2{\lambda }_3^2}\right)\\ +\frac{1}{2{\sigma }_2^2}{\sec }^2\left(\frac{\text{π}{e}_3^2}{2{\lambda }_3^2}\right)e_3{\hat{\Theta }}_2{\Vert S_2\left(Z_2\right)\Vert }^2+\frac{1}{M}{\sec }^2\left(\frac{\text{π}{e}_2^2}{2{\lambda }_2^2}\right){\cos }^2\left(\frac{\text{π}{e}_3^2}{2{\lambda }_3^2}\right)e_2]\end{array}$ (25)

${\stackrel{\dot{}}{\hat{\Theta }}}_2=\frac{1}{2{\sigma }_2^2}{\sec }^4\left(\frac{\text{π}{e}_3^2}{2{\lambda }_3^2}\right)e_3^2{\Vert S_2\left(Z_2\right)\Vert }^2-{\gamma }_2{\hat{\Theta }}_2$ (26)

将(22)~(26)代入(21)可得如下不等式

${\stackrel{\dot{}}{V}}_3\le -{\displaystyle \underset{j=1}{\overset{3}{\sum }}\frac{{\rho }_j{\lambda }_j^2}{\text{π}}\tan \left(\frac{\text{π}{e}_j^2}{2{\lambda }_j^2}\right)}-{\displaystyle \underset{j=1}{\overset{2}{\sum }}{\gamma }_j{\tilde{\Theta }}_j{\hat{\Theta }}_j}+{\displaystyle \underset{j=1}{\overset{2}{\sum }}\frac{{\bar{\epsilon }}_j^2}{2{\upsilon }_j}}+{\displaystyle \underset{j=1}{\overset{2}{\sum }}\frac{{\sigma }_j^2}{2}}$ (27)

根据定义 ${\tilde{\Theta }}_i={\hat{\Theta }}_i-{\Theta }_i^{\ast }$ 和杨氏不等式，如下不等式成立

$-{\gamma }_j{\tilde{\Theta }}_j{\hat{\Theta }}_j\le -{\gamma }_j{\tilde{\Theta }}_j\left({\tilde{\Theta }}_j+{\Theta }_j^{\ast }\right)\le -\frac{{\gamma }_j}{2}{\Vert {\tilde{\Theta }}_j\Vert }^2+\frac{{\gamma }_j}{2}{\Vert {\Theta }_j^{\ast }\Vert }^2$ (28)

联立(27)和(28)，可以进一步得到

${\stackrel{\dot{}}{V}}_3\le -{\displaystyle \underset{j=1}{\overset{3}{\sum }}\frac{{\rho }_j{\lambda }_j^2}{\text{π}}\tan \left(\frac{\text{π}{e}_j^2}{2{\lambda }_j^2}\right)}-{\displaystyle \underset{j=1}{\overset{2}{\sum }}\frac{{\gamma }_j}{2}{\Vert {\tilde{\Theta }}_j\Vert }^2}+{\displaystyle \underset{j=1}{\overset{2}{\sum }}\frac{{\bar{\epsilon }}_j^2}{2{\upsilon }_j}}+{\displaystyle \underset{j=1}{\overset{2}{\sum }}\frac{{\sigma }_j^2}{2}}+{\displaystyle \underset{j=1}{\overset{2}{\sum }}\frac{{\gamma }_j}{2}{\Vert {\Theta }_j^{\ast }\Vert }^2}$ (29)

整合式(6)，(11)和(20)可知

$V_3={\displaystyle \underset{j=1}{\overset{3}{\sum }}\frac{{\lambda }_j^2}{\text{π}}\tan \left(\frac{\text{π}{e}_j^2}{2{\lambda }_j^2}\right)}+\frac{1}{2}{\displaystyle \underset{j=1}{\overset{2}{\sum }}{\tilde{\Theta }}_j^2}$ (30)

因此，如下不等式可以被得到

${\stackrel{\dot{}}{V}}_3\le {\Delta }_1{V}_3+{\Delta }_2$ (31)

其中， ${\Delta }_1=\min \left\{{\rho }_j,{\gamma }_j,j=1,2,3\right\}$ 和 ${\Delta }_2={\displaystyle {\sum }_{j=1}^2{\bar{\epsilon }}_j^2/2{\upsilon }_j}+{\displaystyle {\sum }_{j=1}^2{\sigma }_j^2/2}+{\displaystyle {\sum }_{j=1}^2{\gamma }_j{\Vert {\Theta }_j^{\ast }\Vert }^2/2}$ 。

定理1：在电机系统(1)满足假设条件的情况下，所提出的自适应神经网络控制器能够保证闭环系统中所有信号均为有界的；跟踪误差收敛至原点附近的紧集内；执行器是否存在故障都能保证所有系统状态不超出指定约束范围。

证明：先对式(31)两边乘以 $e^{{\Delta }_{1}t}$ ，在对其进行积分，可以得到

$V_3\le \Pi$ (32)

其中， $\Pi =\left[V_3\left(0\right)-{\Delta }_2/{\Delta }_1\right]e^{-{\Delta }_{1}t}+{\Delta }_2/{\Delta }_1$ 。

根据式(31)和式(32)，可以容易得到 $e_i,i=1,2,3$ 和 ${\hat{\Theta }}_j,j=1,2$ 的有界性。结合定义 $x_1=e_1+y_r$ 和假设2，可以得到 $\left|x_1\right|\le {\lambda }_1+A\le {\psi }_1$ 。从 $e_1$ ， $y_r$ 和 ${\stackrel{\dot{}}{y}}_r$ 的有界性可知，虚拟控制器 ${\chi }_1$ 存在正常数满足 $\left|{\chi }_1\right|\le {\bar{\chi }}_1$ 。类似的过程，可以证明 $\left|x_2\right|\le {\lambda }_2+{\bar{\chi }}_1\le {\psi }_2$ 。控制器和自适应率的有界性也可以通过类似方法证明得到。

从设计的李雅普诺夫函数以及式(30)可知，式(30)中每一项均为正的，因此，如下不等式成立

${\lambda }_1^2\tan \left(\text{π}{e}_1^2/2{\lambda }_1^2\right)/\text{π}\le \Pi$ ，进而在初始值满足 $\left|x_1\left(0\right)\right|<{\psi }_1$ 的条件下可以得到 $e_1\le \sqrt{2{\lambda }_1^2{\tan }^{-1}\left(\Pi \text{π}/{\lambda }_1^2\right)/\text{π}}$ 。通过选取适当的参数可实现跟踪误差 $e_1$ 收敛至任意小。定理1的证明完毕。

4. 仿真实例

为了证明所提出自适应神经网络控制容错方法的有效性，本节针对具有时变状态约束的电机系统展开仿真研究。所考虑的电机系统模型如式(1)。

所考虑的电机系统参数如下： $J=0.01625\text{kg}\cdot {\text{m}}^2$ ， $m=0.506\text{kg}$ ， $R_0=0.023\text{m}$ ， $M_0=0.0434\text{kg}$ ， $L_0=0.305\text{m}$ ， $B_0=0.01625\text{N}\cdot \text{m}\cdot \text{s}/\text{rad}$ ， $L=0.0225\text{H}$ ， $K_{\tau }=3.8\text{N}\cdot \text{m}/\text{A}$ ， $K_B=0.9\text{N}\cdot \text{m}/\text{A}$ ， $R=5\Omega$ ， $G=\text{9}\text{.80665}\text{m}/{\text{s}}^{\text{2}}$ 。通过引入变量 $x_1=q$ ， $x_2=\stackrel{\dot{}}{q}$ 和 $x_3=I$ ，时变约束状态约束 $\left|x_1\right|<0.3\cos \left(0.5\text{π}t\right)+1.2$ ， $\left|x_2\right|<0.4\cos \left(0.2\text{π}t\right)+2$ 和 $\left|x_3\right|<0.1\sin \left(0.6\text{π}t\right)+0.285$ 。参考跟踪轨迹为 $y_r=\sin \left(0.5\text{π}t\right)$ 。

考虑失效故障模型如下：

$\tau =lu,\forall t\ge T$ (33)

其中， $l=0.5$ 和故障发生时间 $T=15\text{s}$ 。

设计控制输入和自适应率如下

$\{\begin{array}{l}{\chi }_1=-\left({\rho }_1+2{\bar{\lambda }}_1\right)\frac{{\lambda }_1^2}{2\text{π}{e}_1}\sin \left(\frac{\text{π}{e}_1^2}{{\lambda }_1^2}\right)-e_1{\bar{\lambda }}_1+{\stackrel{\dot{}}{y}}_r\\ {\chi }_2=-M[\left({\rho }_2+2{\bar{\lambda }}_2\right)\frac{{\lambda }_2^2}{2\text{π}{e}_2}\sin \left(\frac{\text{π}{e}_2^2}{{\lambda }_2^2}\right)+e_2{\bar{\lambda }}_2+\frac{{\upsilon }_1}{2}{e}_2{\sec }^2\left(\frac{\text{π}{e}_2^2}{2{\lambda }_2^2}\right)\\ +\frac{1}{2{\sigma }_1^2}{\sec }^2\left(\frac{\text{π}{e}_2^2}{2{\lambda }_2^2}\right)e_2{\hat{\Theta }}_1{\Vert S_1\left(Z_1\right)\Vert }^2+{\sec }^2\left(\frac{\text{π}{e}_1^2}{2{\lambda }_1^2}\right){\cos }^2\left(\frac{\text{π}{e}_2^2}{2{\lambda }_2^2}\right)e_1]\\ u=-L[\left({\rho }_3+2{\bar{\lambda }}_3\right)\frac{{\lambda }_3^2}{2\text{π}{e}_3}\sin \left(\frac{\text{π}{e}_3^2}{{\lambda }_3^2}\right)+e_3{\bar{\lambda }}_3+\frac{{\upsilon }_2}{2}{e}_3{\sec }^2\left(\frac{\text{π}{e}_3^2}{2{\lambda }_3^2}\right)\\ +\frac{1}{2{\sigma }_2^2}{\sec }^2\left(\frac{\text{π}{e}_3^2}{2{\lambda }_3^2}\right)e_3{\hat{\Theta }}_2{\Vert S_2\left(Z_2\right)\Vert }^2+\frac{1}{M}{\sec }^2\left(\frac{\text{π}{e}_2^2}{2{\lambda }_2^2}\right){\cos }^2\left(\frac{\text{π}{e}_3^2}{2{\lambda }_3^2}\right)e_2]\\ {\stackrel{\dot{}}{\hat{\Theta }}}_i=\frac{1}{2{\sigma }_i^2}{\sec }^4\left(\frac{\text{π}{e}_{i+1}^2}{2{\lambda }_{i+1}^2}\right)e_{i+1}^2{\Vert S_i\left(Z_i\right)\Vert }^2-{\gamma }_i{\hat{\Theta }}_i,i=1,2\end{array}$ (34)

其中，电机系统状态和自适应率初始值为 $x_1\left(0\right)=0.1$ ， $x_2\left(0\right)=0.1$ ， $x_3\left(0\right)=0.05$ ， ${\hat{\Theta }}_1\left(0\right)=0.5$ 和 ${\hat{\Theta }}_2\left(0\right)=0.1$ 。给出设计参数如下： ${\rho }_1={\rho }_2={\rho }_3=12$ ， ${\upsilon }_1={\upsilon }_2=0.2$ ， ${\delta }_1={\delta }_2=1$ ， ${\gamma }_1={\gamma }_2=0.5$ 。

相关仿真结果见图1~6。图1显示了参考跟踪信号，系统输出轨迹及其设定的约束函数。根据图1显示的结果，我们可以看出系统输出很好地跟踪了参考信号。图2和图3分别显示了系统状态x₂和x₃的轨迹。图1~3很好地展示了即使在执行器发生失效故障的情况下，系统状态仍能始终保持在各自指定约束范围内。图4给出了跟踪误差的轨迹，跟踪误差没有超出约束范围。从图5和图6可以看出控制输入和自适应率的有界性。

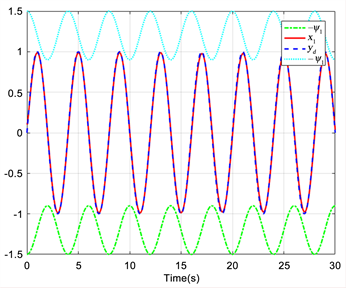
Figure 1. The trajectories of system tracking performance

图1. 系统的跟踪曲线

Figure 2. The trajectories of system state x₂

图2. 系统状态的x₂轨迹

Figure 3. The trajectories of system state x₃

图3. 系统状态x₃的轨迹

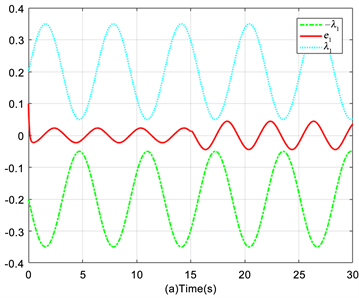
Figure 4. The trajectories of tracking error

图4. 跟踪误差轨迹

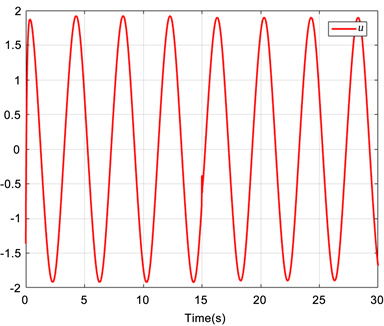
Figure 5. The trajectories of control input

图5. 控制输入轨迹

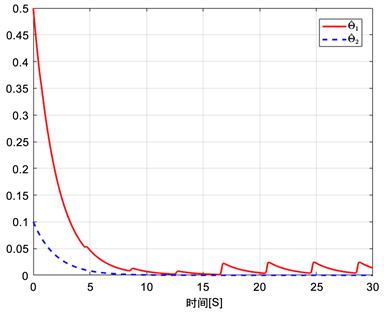
Figure 6. The trajectories of adaptive laws

图6. 自适应率轨迹

5. 结论

本文在自适应控制的框架下，针对具有未知函数的电机系统提出基于障碍李雅普诺夫函数的自适应神经网络容错控制方法。利用神经网络逼近特性，对电机系统中出现的未知函数进行逼近。考虑了执行器可能发生失效故障和偏移故障情况，设计了容错补偿控制策略。为了避免因系统状态过大而引起控制品质减低，甚至系统失稳，在每一步反推设计过程中，引入的时变障碍李雅普诺夫函数保证系统状态始终保持在设定的约束范围之内。通过稳定性分析，证明了所提出的方法能够保证闭环系统中所有信号均是有界的，跟踪误差收敛至原点附近小的紧集内，以及系统状态约束条件未被违反。最后，通过仿真例子进一步证明了所提出方法的有效性。

基金项目

资助项目国家自然基金(61803189, 61622303, 61603164, 61803190)。