1. 引言
下料问题,又称为布局问题(Packing Problem),是指给定一个布局空间和若干待下物体,将待下物体合理地摆放在布局空间中,满足必要的约束条件,并使布局利用率达到最高。下料问题可以指导制造企业的采购计划和生产计划。排样布局的优劣直接与材料成本及经济效益有关 [1] 。二维矩形条带装箱问题(2DR-SPP)是线性的组合优化问题,也是NP-Hard问题,求解难度较大,有重要的研究意义。该问题在计算机辅助设计、图像处理、大规模集成电路逻辑布线设计等领域有广泛应用,有较高的实际使用价值。构建2DR-SPP的简单数学模型,即可实现对中小规模问题的有效求解,又可为研究求解大规模问题的快速高精度的数学规划启发式算法奠定基础有重要的研究价值 [2] 。
P. Yongyingprasert和S. Vasupongayya在处理集群作业调度问题时将其转化为一组二维框打包到大局形容其中的问题,旨在应用二维盒打包算法批处理集群作业调度问题 [3] 。Lam T. Bui、Stephen Baker和Axel Bender为了解决二维(2D)矩形包装问题,引入了一种基于容器的离散化为具有预定义分辨率的单元网格,在添加项目之前,将检查网格单元格是否可以容纳该项目,如果找到合适的空单元群,则添加该项并将其移向容器的左下角。通过将启发式算法与遗传算法(GA)杂交,可以改善项目的顺序和轮换 [4] 。Omar, Mohamed K和Ramakrishnan, Kumaran在考虑无取向的二维料仓包装问题涉及一组需要装入相同矩形料箱的矩形件提出了进化粒子群优化算法(EPSO)来解决非定向二维装箱问题来进行广泛的数值研究以确定最有解决方案 [5] 。在本文中总结已有研究工作的基础上,通过分析切割问题的数学模型和基本属性,说明切割问题属于NP完全问题,结合实际应用中的智能算法来逼近最优解。
2. 模型假设
1) 假设木板厚度和割缝宽度忽略不计。
2) 假设木板厚度与产品厚度一致,即可将其转换成二维装箱问题。
3) 假设生产任务完成后对多余的模板不再进行处理,即恰好完成生产任务。
4) 假设在同一方案下每块木板的切割方式相同,且不会产生误差或可忽略。
3. 符号说明
对于本文所用的符号,这里只列出通用符号,具体符号在引用时会进行具体说明。
4. 模型的建立与求解
4.1. 单产品切割问题
4.1.1. 木板利用率的计算
➢简介
木板利用率的高低是影响企业经济效益的主要因素之一,随着市场竞争的加剧和木板价格的上涨,应该对切割提出更科学的方法,不是简单的“可以切”,而是要“切得块”、“切得好”、“切得省”,通过模板下料的特点提高木板利用率,降低切割成本,从而能为企业获得更多的经济效益
木板利用率越高,即剩余木板面积最小,获得经济效益越高,反之,越低。
➢公式
设木板面积为S,产品面积为
。
则某一块木板的利用率为:
(1)
其中,
表示单一木板利用率,N表示所用木板数量,n表示切割的产品数量。
4.1.2. 平面二维装箱问题“4块法”规划求解模型
➢“4块法”摆放方式介绍
“4块法”就是把二维平面分成4个区域摆放或放置产品,即A、B、C和D四个区域,设置木板长为L,宽为W,产品长为l,宽为w,A区有X1和Y4构成,B区有X2和Y1构成,C区由X4和Y3构成,D区由X3和Y2构成。Xi为产品长在木板长或宽方向上摆放个数,Yi为产品宽在木板长或宽方向上摆放个数。“4块法”摆放方式如图1所示:
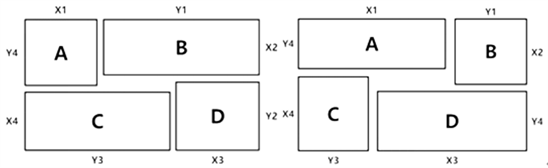
Figure 1. Two layout drawings of “Four blocks method”
图1. “4块法”摆放的两种布置图
➢典型的“4块法”数学模型
“4块法”摆放布置可分为2中类型,一是B和C横向长度之和大于木板长度,此时可能会A和D对角发生矛盾或B和C对角发生矛盾;二是A和D横向程度之和大于木板长度,此时可能会出现B和C对角发生矛盾或A和D对角发生矛盾,矛盾如图2所示。
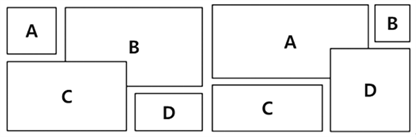
Figure 2. Layout of two contradictory situations
图2. 发生矛盾的两种情况布置图
为了解决这两种矛盾情况,建立以下模型:
目标函数:
(2)
约束条件:
其中,
对于
表示取整符号。
4.1.3. “4块法”规划模型求解
通过Lingo对该线性规划进行求解得到结果如图3所示:
➢结果分析
通过Lingo的求解我们得到
,
,
,
,
,
,
,
,
在增加的四个约束条件下很好地解决了对角矛盾问题,在利用率最高的要求下,实现了木板的充分利用,其利用率为98.3%,具体如表1所示:

Table 1. The result of single product cutting problem
表1. 单产品切割问题的结果
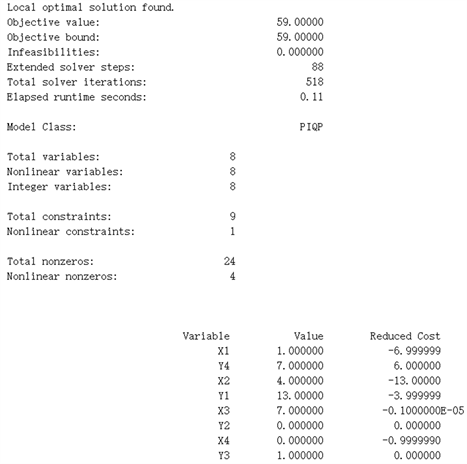
Figure 3. Lingo solution of “four block method”
图3. “4块法”Lingo求解结果
4.2. 双产品切割问题
4.2.1. 组合方式的确定
在进行归纳推理时,通过枚举法我们逐个考察某类方案的所有可能发生值,并根据条件判断答案是否合适,保留合适的,删去不合适的,求解并验证。
Step 1:确定枚举对象
首先,通过单产品切割问题中的模型,在考虑到木板利用率最高的模型下,该木材只切割P1可以切割59块,同样的,该木材只切割P3可以切割48块,为减少枚举的次数,我们以P3的数量作为枚举对象。
Step 2:确定枚举范围
对于产品P1的范围为[0, 59],产品P2的范围为[0, 48],且根据实际情况我们知道,产品P1和产品P2的数量都为整数。
Step 3:确定判定条件
对逐一枚举的可能的解要满足二维多产品装箱模型,如果满足,继续进行Step 4,如果不满足,将P1的数量减一输出并返回到Step 2。
Step 4:计算木板利用率
通过公式(1)对木板利用率进行求解,并比较结果大小,依次选取最大的结果进行填表。
4.2.2. 建立二维多产品装箱模型
二维多产品装箱问题,是指一系列二维平面图形互不交叉的放置在某一板材上,使得所覆盖的板材面积最大,对于企业而言,板材的利用率越高,越节约材料,所用成本越少,对提高企业经济效益起到关键作用。
➢确定优化目标
· 对于企业来说,为使经济效益达到最高,要使木材利用率达到最高,即生于模板面积最小。
· 对于模板来说,产品P1和P2的组合要能在一张木板上实现。
➢确定排放原则
将所需产品排放在定长定宽的木板中,产品的长或宽与木板平行,产品之间不可交叉,且不得超过木板的长或宽。
➢二维多产品装箱模型的建立
假设木板的长度为L,宽为W,面积为S,需要切割的小板材长为
,宽为
,i表示第i种需要切割的小板材,
,板材剩余面积为Areal。当零件横放时占用的空间为
竖放占用的空间是
。
表示在原料板上第j块区域内横放零件的行数;
表示板材上第j块区域内小板材竖放的行数。
表示板材上第j块区域内零件横放时每行的个数;
表示大板材上第j块区域内小板材竖放时每行的个数,则:
目标函数:
(4)
限制条件:
(5)
4.2.3. 基于贪心算法求解二维装箱问题
➢贪心策略的基本思想
定义:贪心法是一种解决最优问题的策略。它是从问题的初始解出发,按照当前最佳的选择,把问题归纳为更小的相似的子问题,并使子问题最优,再由子问题来推导出全局最优解。
使用贪心方法需要注意局部最优与全局最优的关系,选择当前状态的局部最优并不一定能推导出问题的全局最优。
➢贪心算法求解的三个步骤
Step 1:确定贪心策略;
Step 2:根据贪心策略,迭代得到局部最优解;
Step 3:将局部最优解合并起来就得到全局最优解。
➢贪心策略的特点
· 贪心选择性质:所求问题的整体最优解可以通过一系列局部最优的选择来达到,这样的选择称为贪心选择。这些选择只依赖于以往所做过的选择,决不依赖于将来的选择。
· 最优子结构性质:当一个问题的最优解包含其子问题的最优解时,称此问题具有最优子结构性质。
4.2.4. 结果分析与结论
通过枚举得到相关组合为如表2所示:

Table 2. Enumeration combination scheme
表2. 枚举组合方案
➢结果分析
通过对上述结果进行分析,我们可以知道在一块木板上切割P1和P3产品的优化组合有44种,且满足二维多产品装箱模型,通过贪心算法对二维多产品装箱模型进行求解得到相关组合方式,得出给出按照木板利用率由高到低排序的前3种切割方案,利用率由高到低的排列为:99.17%、98.50%以及98.30%,具体结果如表3所示:

Table 3. Result of multi-product cutting problem results of multi-product cutting problem
表3. 多产品切割问题的结果
4.3. 满足任务数要求的双产品切割问题
4.3.1. 总利用率的计算
➢简介
木板利用率的高低是影响企业经济效益的主要因素之一,随着市场竞争的加剧和木板价格的上涨,应该对切割提出更科学的方法。在实际生产中,往往不是对单一木板进行切割,而是在不同组合方式的切割下要求总利用率尽可能高。
木板总利用率越高,即剩余木板面积最小,获得经济效益越高,反之,越低。
➢公式
设木板面积为S,产品面积分别为
。
则木板总利用率为:
(6)
其中,
表示木板总利用率,N表示所用木板数量,
表示切割的产品数量。
4.3.2. 构建基于生产任务下的二维装箱模型
因此,矩形件套料问题的数学模型如下:
目标函数:
(7)
约束条件:
(8)
(9)
(10)
(11)
其中,(8)、(9)表示所有木板均能在大木板完整割取,没有超出大木板的边界;式(10)表示各木板之间互不重叠;式(11)表示所有矩形件虽大小不一,但都有一定的面积。所以,最好的套料结果就是各木板之间既不重叠也无空隙,即
(12)
4.3.3. 最左下占角动作放置策略
➢基本思想
在某一时刻,已经按分割规则把大木板矩形分了若干块,那么对还未分割的部分,最好是占据某个角,其次是贴边,最差的是悬空。我们采用的算法即在分割大木板时,总是先分某个角,这样分割就可减小对空间的浪费。
同时,也避免了基于遗传算法的BL启发式策略中当较大矩形产品在连续移动时受阻,会在模板中产生许多空区域以及产品可与之前排好的产品分别形成一个角区的缺点。
➢基本概念
① 格局:在某一时刻,大木板已经互不重叠地分割了若干木板,这种状态,称为一个格局。偌大木板还未分割,此时的格局称为初始格局;若大木板无法再分割,此时的格局称为终止格局。
② 占角动作:在某一格局下,若即将分割的木板R与大木板剩余部分的边有重叠(并且重叠的长度大于0),则称分割木板的这种作法为一个占角动作。
③ 两矩形块间的距离:在两木板Ri和Rj,中各取一点
,
,设这两点间的曼哈顿距离
为Lij,则两木板间的距离
。
④ 占角动作的穴度:如图4所示,若将木板Ri按合法占角动作分割走后,Ri与形成这个角以外的其它部分的距离的最小值为
,
和
分别为木板的宽和长。则此占角动作的穴度Ci定义为
(13)
占角动作的穴度反映了即将分割的木板和大木板已有分走的抱紧程度,穴度越大,就抱得越紧,在选择占角动作时,就选穴度最大的占角动作。
⑤ 占角动作的贴边数:设某一占角动作所关联的木板为R,那么与R贴边的木板块数称为该占角动作的贴边数。
➢占角动作选择原则
为了将木板在大木板中一个“好”的位置和方向上割取,则必须制定一些好的规则,BLCO放置策略中的主要规则如下:
规则1:选择最向下向左的动作。
规则2:选择对应动作矩形件占领角区面积最大的占角动作。
规则3:选择对应动作矩形件面积最大的占角动作。
规则4:若对应动作矩形件既可横放,也可竖放,则选择横放的占角动作。
规则5:选择对应动作矩形件序号最小的占角动作。
BLCO策略的核心体现在规则1和2上,即选择最向下向左的动作和选择角区面积最大的占角动作,若规则1和2无法再起作用,则采用规则3、4和5打破僵局,从而选出唯一的占角动作。
4.3.4. 全局搜索的GA算法
➢简介
遗传算法(Genetic algorithm, GA)是智能优化方法中应用最广泛的算法,也是目前发展最为成功的智能算法之一。GA算法是由Holland教授1970年代提出来的,其中最为重要的就是模式定理(schema theorem),所借鉴的生物学基础就是生物的进化和遗传。下面从GA算法的数学基础与收敛理论两个方面进行描述,并总结出GA算法的特点、不足及改进方法。
➢原理
① 染色体编码与解码:染色体编码是遗传算法最关键的步骤,其是一种可以将实际待优化问题的可行解转化到遗传算法可以处理的搜索空间中的一种方法。
② 种群初始化:随机产生N个染色体作为初始种群,遗传过程中的收敛速度会受到初始种群大小的影响,因此N的取值应选择适当,本文N选取60。
③ 适应度函数:适应度函数指引着遗传算法的搜索方向,适应度函数的选择应该根据具体的问题而定,本研究中适应度函数为木板总利用率,即为目标函数。
④ 遗传算子
· 选择算子:轮盘赌选择算法是遗传算法中最常用的选择算法,其根据群体中每个染色体的适应值得到群体所有染色体的适应值总和,并分别计算每个染色体适应值与群体适应值总和的比;较优染色体的值较大,被选择的概率就相对较大。
· 交叉算子:交叉操作是遗传算法中的核心操作步骤,是种群中产生新个体的主要途径之一。一般情况下,设置交叉概率为0.4~0.9之间。
· 变异算子:在遗传算法中,产生新一代的个体主要依靠的是选择和交叉,变异操作是一种产生多样性个体的辅助手段,变异算子设计的好坏能决定算法的局部搜索能力。变异概率较小,一般设为0.0001~0.1之间。
在遗传算子的操作下被选择、交叉与变异,形成高阶的、高于群体平均适应值的模式(较优解),最终接近全局最优解。所以,GA算法是一种基于自然法则和遗传机制的智能优化算法,并且基于群体进行搜索,其基本流程如图5所示。
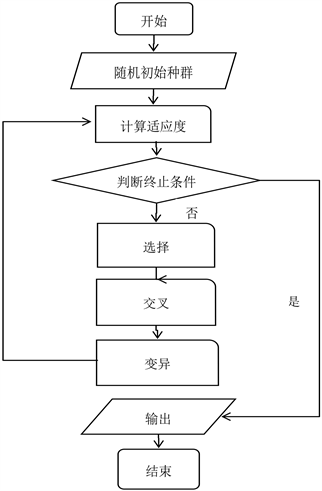
Figure 5. The basic flow chart of the algorithm GA
图5. GA算法基本流程图
从上图可知,GA算法从随机产生的初始种群开始搜索,分别计算每个个体的适应值,进而判断个体的优劣,通过选择算子选出较优秀的个体,通过交叉运算和变异运算产生后代,再重新计算每个新个体的适应值,从而判断是否收敛到最优解。如果满足终止条件,则搜索到最优个体。
4.3.5. 模型的求解与结果分析
基于多产品切割问题中对P1和P3排列组合的44种方式,通过遗传算法(GA)对全局最优解进行搜索,在木板总利用率最高的目标前提下,从初代种群开始搜索,分别计算每个个体的适应值,进而判断个体的优劣,通过选择算子选出较优秀的个体,通过交叉运算和变异运算产生后代,再重新计算每个新个体的适应值,从而判断是否收敛到最优解,从而搜索得到最优个体,其组合结果如图6所示:
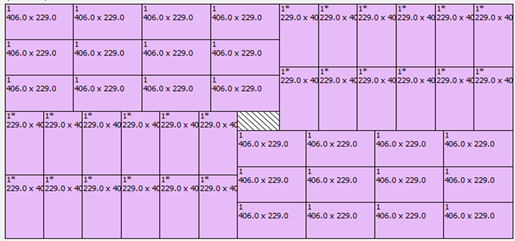
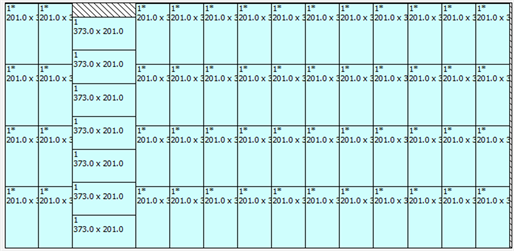
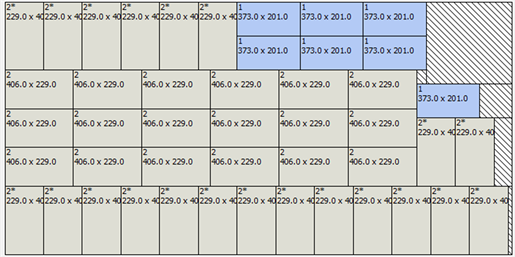
Figure 6. Optimal cutting scheme for multiproduct cutting problem
图6. 多产品切割问题的切割最优方案
➢结果分析
通过对上述结果进行分析,为完成P1和P3的生产任务,加入生产任务的限制条件,我们得到木板利用率最高的前提下的三种排列组合方案,每种组合只需用一块木板,且第一块木板利用率为99.17%,第二块木板的利用率为98.29%,第三块模板的利用率为92.23%,得出总利用率,具体结果如表4所示。

Table 4. Result of double product cutting problem meeting task number requirements
表4. 满足任务数要求的双产品切割问题的结果
4.4. 多产品切个问题
4.4.1. 多产品切割模型的准备
遗传算法在小范围内求解全局最优解具有效率高、准确性高的特点,但是对于大范围的求解显示遗传算法的效率不那么明显,在满足任务数要求的双产品切割问题中只有44种排列组合方式,运用遗传算法(GA)可以满足效率要求,但是对于四种产品的组合数量5355312 (59 × 31 × 48 × 61)显然已经不满足要求,在此基础上通过分析遗传算法(GA)和求解局部最优解所用方法模拟退火算法(SA)的缺点和不足,提出一种混合GA算法和SA算法的HGASA算法。
4.4.2. 混合GA算法和SA算法的HGASA算法
➢简介
HGASA算法:借鉴Memetic算法的思想,混合GA算法和SA算法的HGASA算法的一种新算法,其最主要的思想就是融合了GA算法的全局索搜索Negligence和SA算法的局部搜索能力。
➢原理
矩形件套料中,产品的套料次序和各自选装角度是影响套料切割的重要因素。采用HGASA算法,通过全局优化概率产生最佳的套料次序和每个举行见的旋转角度,然后采用BLCO放置策略进行排放和定位,再通过局部搜索过程,循环往复,最终实现自动套料,其基本流程如图7所示:
4.4.3. 模型的求解与结果分析
基于遗传算法(GA)改进的混合GA算法和SA算法的HGASA算法能够更加高效的找到四种产品的最优排列组合,该算法首先通过全局优化概率产生最佳矩形件排列顺序和每个矩形件对应的旋转角度,然后利用BLOC放置策略进行排放和定位,并计算其适应函数值,再利用GA算法对当前方案进行交叉变异,执行最优方案的局部搜索过程,循环迭代直到满足终止条件为止,最终实现对最优切割方案的求解,因篇幅所限此处只列出一种排版方案,如图8所示:
➢结果分析
通过对上述结果进行分析,为完成四种产品的生产任务,我们得到木板利用率最高的前提下的排列组合方案,方案1需要41块木板,每块木板的利用率为98.51%;方案1需要41块木板,每块木板的利用率为98.51%;方案2需要5块木板,每块木板的利用率为98.29%;方案3需要1块木板,每块木板的利用率为98.10%;方案4需要11块木板,每块木板的利用率为97.55%;方案5需要71块木板,每块木板的利用率为96.86%;方案6需要1块木板,每块木板的利用率为96.53%;方案7需要1块木板,每块木板的利用率为95.06%;方案8需要8块木板,每块木板的利用率为92.66%;方案9需要1块木板,每块木板的利用率为76.40%,进而得出总利用率,具体结果如表5所示:
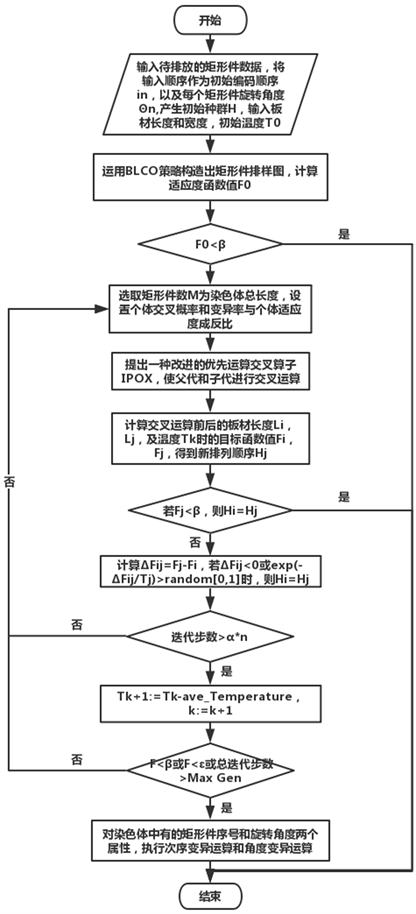
Figure 7. Flow chart of algorithm HGASA
图7. HGASA算法流程图
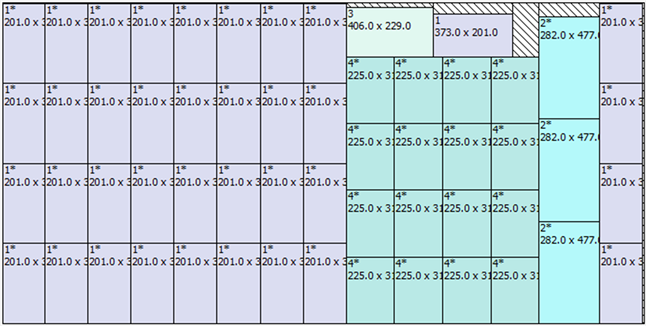
Figure 8. Optimal cutting scheme for multiproduct cutting problem
图8. 多产品切割问题的切割最优方案

Table 5. Result of multi-product cutting problem
表5. 多产品切割问题的结果
5. 模型的评价与推广
5.1. 模型的评价
5.1.1. 模型的优点
1) 本文所运用的混合GA算法和SA算法的结合了GA算法和SA算法的优点,在SA算法的基础上那个找到局部最优解,通过GA算法得到全局最优解,能够快速高效的得到方案在整体上的全局最优解。
2) 在选择组合方案时,通过MATLAB对与单一产品的利润进行对比,在利润最大化的基础上对组合方案进行判定,对模型进行简化,大大减少了运行双目标二维平面装箱模型的时间。
3) 在“4块法”摆放的对角矛盾中,通过增加限制条件,解决对角矛盾。
5.1.2. 模型的缺点
在“4块法”摆放中为解决对角矛盾增加的限制条件,缩小了求解范围,影响力全局优化程度。
5.2. 模型的推广
在三维集装箱装载问题中,设集装箱的尺寸分别为L (长)、W (宽)、H (高),同时其最大装载容积和最大装载质量分别用V和G表达。待装载的货物数量设为n,其对应的尺寸参数与质量分别用
,
,
,
表示。
在关于装箱问题的描述中,装载利用率受各种复杂因素的影响与约束,根据现在关于装箱问题的研究,本文对复杂的影响因素总结如下:
· 货物放置方向约束:即货物在装载过程中受到装载方向的约束。
· 货物装载容积约束:即货物总体积不能超过集装箱的最大装载容积。
· 货物装载质量约束:即货物在装载过程中其总质量不能超过集装箱的最大允许装载质量。
· 货物的装载顺序约束:即须根据一定的优先性来装载货物,例如先进后出。
· 稳定性约束:即货物的重心必须保持在一定的范围内,保证货物的稳定性。