1. 引言
滑行时间是指航空器在机场跑道资源与停机位资源之间的运行时间,其作为衡量航空器场面运行效率的关键指标,在预测滑行延误、辅助航班排序、控制推出活动等方面发挥着重要的辅助决策作用 [1]。在大型繁忙机场系统中,场面运行具有大流量、高密度、小间隔等显著特征,进离场活动之间的交互运行使得滑行道使用冲突和航空器运行冲突问题频发。特别是对于离场航空器而言,因其滑行过程存在诸多的随机、动态和多变因素,离场滑行时间的预测精度通常较低,航空器过早或过晚地推出机位可能会产生不必要的关舱门等待、滑行道等待和跑道头等待,从而导致离场航空器的场面运行效率较为低下,伴随而来的场面冲突、机场拥堵和航班延误等一系列问题已成为当前及未来困扰世界航空运输业的重难点和关键点问题 [2]。因此,为显著提升机场场面滑行性能、科学支撑航空运输管理决策、有效缓解机场拥堵延误现状,亟需对离场航空器的场面滑行时间进行准确预测。
航空器离场滑行时间预测问题研究最早可追溯到20世纪90年代,Shumsky将航空公司、跑道使用、交通需求作为影响航空器滑行时间的主要因素,提出了离场滑行时间预测问题的线性回归模型,针对两种不同的测度方法进行了综合对比分析 [3]。Herbert等人针对航空器离场过程,将离场需求表示为非齐次泊松过程,服务时间建模为指数分布随机变量,对起飞队列长度以及航空器拥堵进行了建模分析 [4]。2001年,麻省理工学院Idris等人分析了影响离场航空器滑行时间的各类因素,研究并建立了离场滑出时间与起飞航空器数量之间的线性关系 [5]。除了数据统计方法之外,计算机仿真方法亦被用于场面滑行网络运行模拟和滑行时间预测分析。例如,尹嘉男针对平行跑道机场系统,建立了场面网络拓扑模型和交通流生成模型,对航空器场面滑行时间进行了仿真计算 [6] ;Lee等人采用离散事件快速仿真方法对航空器滑行时间进行了预测,并在实时环境应用之前采用仿真数据对滑行性能进行了评估 [7]。另外,Balakrishna等人建立了基于增强型学习算法的离场航空器滑出时间预测框架,针对不同的机场运行场景,对离场航空器的滑出时间进行了预测 [8]。Yin等人采用多种机器学习方法对航空器滑行时间进行了预测,并对不同方法的预测精度进行了综合对比分析 [9]。在应用层面,美欧航空运输业亦提出了相关的航空器滑行时间预测方法,例如美国的滑动平均法 [5] 和欧洲的可变滑行时间统计法 [10] ,这些方法在机场运行管理和空中交通管理决策中取得了良好的应用成效。
通过国内外理论研究与业界应用分析发现,当前对离场滑行时间预测的研究主要停留在某个指标与滑行时间的单因素相关分析方面,而且预测变量主要聚焦离场航空器,而忽略了进场航空器滑行活动对离场滑行时间的影响。事实上,场面滑行涉及进离场航空器之间的协同交互,仅采用离场交通流统计指标对离场滑行时间进行预测的思路限制了预测性能的进一步提升。另外,文献追踪显示:提升树(Boosting Tree)算法作为机器学习领域内一种主流的集成学习方法,目前仍未广泛地应用于航空器滑行时间预测问题研究。鉴于上述原因,本文充分考虑进场航空器运行对离场航空器场面滑行时间的影响,建立基于提升树模型的航空器离场滑行时间预测方法,以期提升复杂机场系统内离场航空器的场面滑行性能,并为航空器滑行时间预测提供一种新的研究思路。
2. 模型输入与输出
2.1. 数据集
本文的数据集来源于中国典型的复杂民用机场系统——上海浦东国际机场,不失一般性,选取2014年10月1日至10月16日的17,986架航班的运行数据作为离场滑行时间的训练和预测样本。其中,包括8970架离场航班和9016架进场航班,进离场航班信息总体统计情况如图1所示。
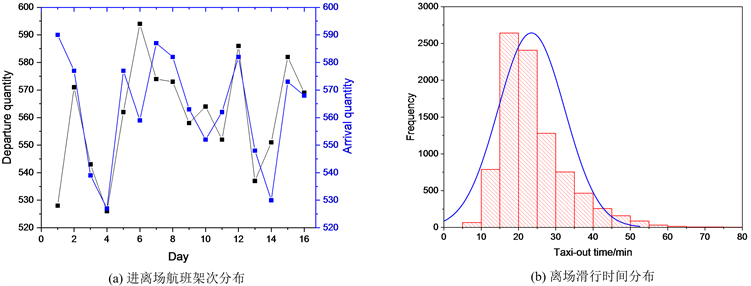
Figure 1. Aggregate statistics of flight information in Shanghai Pudong international airport dataset
图1. 上海浦东国际机场数据集航班信息总体统计
浦东机场样本集中单日进离场航班的总架次保持在1100架左右,且平均离场滑行时间为23.5分钟,单架航班离场滑行时间超过30分钟的比例为17.9%。可以看出,浦东机场当前仍有较高比例的离场航班具有较大的滑行时间,原因可能在于:航班因场面运行预测不准确导致过早或过晚推出停机位,从而在滑行过程中与其它航班之间存在较多的资源使用冲突,进而引发长时间的滑行等待。不失一般性,本文选取某日离场航班为预测对象,并对其它所有运行日的数据进行训练,得到相应的滑行时间预测模型。针对上述数据集,具体的样本划分情况如下:
1) 训练样本:2014年10月1日至10月15日,包括8401/8448架离场/进场航班;
2) 预测样本:2014年10月16日,包括569/568架离场/进场航班;
3) 预测个体:2014年10月16日,随机选取300架离场航班。
在样本训练过程中,采用10折交叉验证方法对训练样本进行动态分组,以对提升树方法训练得到的离场滑行时间机器学习模型进行多重验证分析。
2.2. 预测变量
预测变量主要聚焦交通流宏观统计视角,重点选取4类影响离场滑行时间的特征指标,分别为:场面瞬时流量、场面累计流量、起降队列长度、时隙资源需求。根据进离场统计对象的不同,上述4类指标可进一步细分为8个变量,其中“离场”相关指标的统计对象仅聚焦离场航空器,“进场”相关指标的统计对象则仅聚焦进场航空器。具体计算方法如下:
1) 场面瞬时流量:指航空器在推出或降落时刻正在场面滑行的离场/进场航空器数量,分为离场瞬时流量和进场瞬时流量。根据该指标定义可知,航空器统计范围包括已经推出且尚未起飞的离场航空器、已经降落且尚未轮挡的进场航空器。
2) 场面累计流量:指航空器在整个滑行过程中场面上曾经或正在处于滑行状态的离场/进场航空器数量,分为离场累计流量和进场累计流量。根据该指标定义可知,航空器统计范围包括滑行过程与待预测航空器滑行过程存在时间交集的离场航空器或进场航空器。
3) 起降队列长度:指航空器在整个滑行过程中起飞/降落的航空器数量,分为起飞队列长度和降落队列长度。根据该指标定义可知,航空器统计范围包括起飞时刻处于待预测航空器滑行过程的离场航空器、降落时刻处于待预测航空器滑行过程的进场航空器。
4) 时隙资源需求:指在以航空器推出时刻或降落时刻为中心确定的某一特定范围内,处于推出或降落状态的离场/进场航空器数量,可分为离场时隙需求和进场时隙需求。考虑进离场航空器的场面滑行时间,本文将该范围设定为30分钟 [11]。根据该指标定义可知,航空器统计范围包括降落时刻处于待预测航空器时隙内的进场航空器、推出时刻处于待预测航空器时隙内的离场航空器。
2.3. 响应变量
响应变量为离场航空器的滑行时间,即起飞时间与撤轮挡时间之间的差值。针对2.1节中的训练样本,以2.2节中的8个预测变量为输入,建立离场滑行时间机器学习模型,对2.1节预测样本中的300个预测个体的离场滑行时间进行预测,并输出每一架离场航班的预测结果。
3. 机器学习训练模型
本文采用提升树方法对航空器离场滑行时间预测问题进行建模。提升树方法作为一种集成学习方法,兼具AdaBoost算法和分类回归树(CART)算法两者的优势,可重复利用已有的训练数据集信息,在训练数据不足的情况下亦可保持较高的预测精度 [12]。提升树模型降低了机器学习调参的工作量,继承了CART树对训练数据进行最优切分的规则,可有效避免过拟合现象并提高泛化能力。
3.1. 提升树模型
提升树模型对加法模型(基函数的线性拟合)和前向分布算法进行了融合,且基函数的建立采用决策树算法,本文针对数据集中的进离场航班,建立滑行时间预测问题的二叉回归树。将提升树模型表示为决策树的加法模型:
(1)
其中,
为决策树,
为决策树的参数,M为树的个数。
假设模型输入信息为
,输出信息为
。提升树算法采用前向分布算法,对于初始状态,将初始提升树设置为:
(2)
对于
,第m步的提升树模型
将基于上一步的模型
进行建立
(3)
为确定下一颗决策树的参数
,建立经验风险最小化模型
(4)
其中,L为平方误差损失函数,具体表达式为:
(5)
结合式(5)对式(4)进行更新,则新的损失函数为:
(6)
(7)
可以看出,在提升树回归建模过程中,每次回归树的迭代生成所采用的训练数据均为上次预测结果与训练数据值之间的残差,且该残差将随着迭代过程不断减小。
3.2. 训练结果分析
根据3.1节中阐述的机器学习方法,对2.1节中的数据集进行训练。考虑到原始的训练样本中存在滑行时间过大的异常值,本文从训练样本中的8401架离场航班中剔除28架滑行时间≥60分钟的航班,形成最终的训练样本以提升机器学习算法的预测精度。图2所示为基于提升树模型得到的航班离场滑行时间预测机器学习模型的训练结果统计情况。
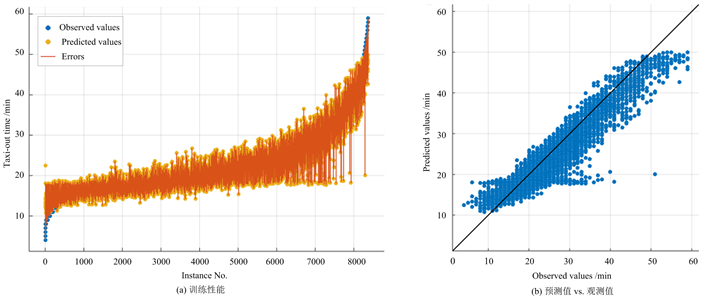
Figure 2. Aggregate statistics of flight information in Shanghai Pudong international airport dataset
图2. 上海浦东国际机场数据集航班信息总体统计
本文建立的基于提升树模型的机器学习算法的运行时间为5.3秒,具有较高的训练效率,可应用于(预)战术层面的机场运行管理和空中交通管理等决策过程。图2(a)中预测值与观测值的差异体现了提升树算法在避免过拟合方面的优势,而图2(b)则表明了训练模型预测值与观测值之间较强的线性相关性。同时,训练模型的拟合优度R2 = 0.87,考虑到2.2节中选用的8个预测变量均为交通流相关的宏观总量参数,在尚未考虑机场布局相关特征指标的情况下,该拟合优度已达到了较为满意的训练效果。
4. 实例验证分析
针对第3节得到的基于提升树模型的离场滑行时间机器学习训练模型,对2.1节中300个预测个体的离场滑行时间进行预测,并建立均方根误差(RMSE)、平均绝对误差(MAE)、平均误差(MD)和标准差(SD)等多个性能指标对训练模型的预测性能进行综合分析。
4.1. 预测结果
图3所示为300个预测个体对应的离场滑行时间预测值与实际观测值的对比情况,以及预测误差的分布统计情况。其中,预测误差定义为预测值与观测值之差。图3(a)中具有正误差和负误差的航空器数量分别为110架和190架,可以看出基于提升树模型的机器学习方法对更大比例航空器的离场滑行时间预测结果高于实际观测结果。在正误差统计范围内,最大和最小的误差分别为5.76分钟和0.01分钟;在负误差统计范围内,最大和最小的绝对值误差分别为11.40分钟和0.05分钟。图3(b)中预测误差的平均值在−1.0分钟附近,且具有显著的正态分布特性。

Figure 3. Prediction performance of machine learning model for taxi-out time prediction
图3. 离场滑行时间预测机器学习模型的预测性能
4.2. 精度分析
为评价训练所得的机器学习模型的预测性能,建立均方根误差(RMSE)、平均绝对误差(MAE)、平均误差(MD)和标准差(SD)四个评估指标,具体计算方法如下:
(8)
(9)
(10)
(11)
其中,n为待预测滑行时间的离场航班数量,
和
分别为离场航班i滑行时间的预测值和观测值。
根据式(8)~式(11),对300个预测个体的离场滑行时间的预测误差进行计算。表1和表2所示为离场滑行时间预测机器学习模型的精度分析,以及在不同误差范围内的离场航空器占比统计情况。

Table 1. Precision analysis of machine learning model for taxi-out time prediction
表1. 离场滑行时间预测机器学习模型的精度分析

Table 2. Departure aircraft statistics under different error ranges
表2. 不同误差范围内的离场航空器占比统计
由表1可以看出,均方根误差为2.62分钟,表明预测过程中不存在特大或特小的误差。平均绝对误差和平均误差分别为2.05分钟和−1.02分钟,结合图3(a)中预测结果高于实际观测结果的航班比例较大这一情况,说明较小比例的负误差的航班个体却具有相对较大的绝对值误差。表2显示本文采用的基于提升树模型的航空器离场滑行时间预测方法可将94%的航班预测误差控制在
分钟范围之内,将78%的航班预测误差控制在
分钟范围之内,具有较高的预测精度。与国内外航空运输业界常用的滑动平均方法、数学平均方法相比,本文所提方法具有绝对的优势。与当前其它的理论方法相比,本文所提方法在保持算法高效、预测变量计算可行的条件下亦可保持较高的预测精度。
5. 结论
1) 在复杂的高密度机场系统内,离场航空器场面运行随机、动态和多变,对其滑行时间进行准确预测有助于预测滑行延误、辅助航班排序、控制推出活动,降低关舱门等待、滑行道等待和跑道头等待时间,进而缓解飞行冲突和机场拥堵等问题。
2) 考虑进场航空器场面运行对离场航空器滑行时间的影响,建立了涵盖四大类、八小类的滑行影响因素特征指标体系,采用提升树方法对离场滑行时间进行了机器学习建模,上海浦东国际机场实例分析验证了所提方法具有较低的计算成本和较高的准确度。
3) 在预测变量计算可行的条件下,所提方法可有效应用于预战术层面的离场航空器滑行时间预估,以及战术层面的滑行时间动态估计。
4) 所提方法对任意时间粒度、任意机场系统的航空器离场滑行时间预测问题均具有普适性。
基金项目
中国博士后科学基金面上资助项目(2017M611809),江苏省博士后科研资助计划(1701099C)。