1. 引言
随着人们对天体目标的不断探索,望远镜的功能指标要求越来越高,大口径望远镜由于对空间目标的分辨能力具有优势,因此其是科学界研究的主要方向 [1] [2] [3] 。大口径望远镜系统一般成像光程较长,主光路需要经过coude系统内多块反射镜的折转后在coude焦面成像。在望远镜跟踪天体目标过程中,由于俯仰、方位轴的转动会导致主光路在coude各反射镜上发生多次旋转,从而导致望远镜焦面产生像旋。为此,需要在望远镜主光路中引入消像旋装置,LBT、Hooker、JCMT等大口径望远镜均采用K镜消旋方式,如图1所示。
国内外相关专家及学者对望远镜消旋问题开展了许多研究 [4] [5] [6] [7] 。中国科学院云南天文台研究人员曾根据光线追迹和矩阵光学的方法分析了望远镜像方视场旋转,并将地平式望远镜由地球自转引起的物方视场旋转进行了理论推导,这些研究成果为修正像旋提供了理论依据 [8] ;中国科学院国家天文台研究人员分析了K镜的消旋原理及条件,并利用Zamax及Matlab对K镜的光学设计及误差补偿进行深入研究 [9] ;中科院长春光学精密机械与物理研究所对消旋K镜支撑结构开展研究,对其支撑点位置进行优化,保证K镜内部光学元件的面形精度 [10] ;国外方面,A. Brunelli [4] 等人对K镜消旋系统反射镜支撑及调整结构进行了详细的研究;4 m望远镜项目“4 m DAG telescope”研究团队对望远镜的像旋问题也开展研究,分别对消旋K镜的光机结构以及驱动环节进行了设计,并进行了仿真分析 [11] 。此外,E-ELT、SONG Telescope等大望远镜研究团队消像旋问题开展了一定的研究 [12] [13] 。
本文在充分整理和总结国内外相关文献研究的基础上,针对2 m地平式望远镜像方视场旋转问题设计了消旋K镜装置,对消旋K镜作用矩阵模型、初始零位及旋转规则、准直精度等问题展开深入研究,并进行了K镜准直装调实验,以验证本文所研究成果的有效性及正确性。
 (a) K mirror in JCMT
(a) K mirror in JCMT  (b) k mirror in Hooker
(b) k mirror in Hooker  (c) k mirror in LBT
(c) k mirror in LBT
Figure 1. The K mirror in large aperture telescope
图1. 大口径望远镜中的消旋K镜装置
2. K镜光学消旋数学模型
我们首先根据光学矩阵传递的原理建立K镜消旋的理论模型,设K镜入射光矢量为A,出射光矢量为
,光线通过K镜依次在K1、K2、K3反射镜上发生折转,各反射镜的法线向量单位矩阵分别为
、
、
,各反射镜作用矩阵为
、
、
,反射镜作用矩阵与反射镜法线单位矩阵的关系为 [14] :
(1)
其中:
(2)
则K镜出射光与入射光矢量矩阵具有如下关系:
(3)
若入射光矢量A沿光轴方向旋转角度
,K镜相应地沿光轴旋转
,则入射光A为:
(4)
K镜中,K1、K2、K3反射镜作用矩阵则相应地变为:
(5)
K镜系统内部光学元件的位置关系一般满足一下条件:
(6)
将公式1、公式2、公式5带入公式3中,则可推导出射光矢量
为:
(7)
即入射光经过K镜后在X向发生镜像,但没有发生旋转。
在K镜安装及准直装调的过程中,由于机械结构的加工误差以及准直误差,不能严格保证公式6所定义的各反射镜的位置关系。若K镜各反射镜偏离理想位置,如图2所示,我们推导各反射镜位置关系。
由公式7可知,K镜系统作用矩阵应该满足以下关系:
(8)
将公式1、公式2代入公式8中,则可得:
(9)
从公式9可以推出,若各反射镜位置满足公式10所表示的关系,K镜的传递矩阵没有改变,即K镜同样具有消旋作用。
(10)
公式10说明K镜安装过程中,各反射镜允许出现倾斜偏差,因此在一定程度上降低了K镜机械加工中的精度要求,同时对K镜的准直装调具有一定的指导意义。
3. K镜消旋策略研究
消旋K镜系统安装在国内某地基2 m口径望远镜coude光路的M6镜之后,2 m望远镜主光路图如图3所示。在跟踪观测目标过程中,由于主光路需要经过coude系统多片平面镜的折转,目标在coude焦点处会产生像方视场旋转,通过上节中推导的K镜光路传递矩阵可知,在coude光路中引入K镜系统可以消除被观测目标在coude像面的旋转,但若要准确得到消旋K镜的旋转规则,需要推导出望远镜入射光经coude光路后产生的像旋与望远镜俯仰轴、方位轴旋转的关系,我们本节对以上问题展开深入研究。
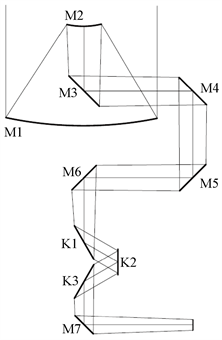
Figure 3. Light path of 2m telescope
图3. 2 m望远镜主光路图
2 m望远镜采用地平坐标,A为方位角,从正北向东计量,范围0˚~360˚,对应于方位轴的转动。Z为天顶距,从天顶向前下方计量,范围为0˚~90˚,对应于俯仰轴的转动。定义望远镜主光路入瞳处坐标系为o-xyz,坐标系中角度的方向,迎着光线(逆光)观察逆时针方向为正方向。从坐标系o-xyz中分别发出四条光线x+、x−、y+、y−,沿主光路方向最终汇聚至coude像面,光线坐标系o-xyz经过M3、M4、M5、M6、M7镜之后分别形成局部坐标系o3-x3y3z3、o4-x4y4z4、o5-x5y5z5、o6-x6y6z6、o7-x7y7z7。如图4所示。

Figure 4. COUDE path of 2 m telescope
图4. 2 m望远镜coude光路图
M3镜固定在2 m主镜之上,其随望远镜方位轴及俯仰轴转动,M4、M5、M6镜安装在望远镜水平轴立柱上,其随望远镜方位轴转动,当望远镜俯仰轴旋转时,其保持固定状态。K镜放置于M6镜之后,因此我们要建立主光路经过M6镜之后的像面旋转与望远镜俯仰轴、方位轴旋转的关系。
当方位轴旋转时,则方位角A变化,在∆t时间内,方位角变化+∆A,从正北向东方向转动。入射光在M3镜发生折转,即从x+向y+旋转,按照光线追迹推导,入射光经过M6镜之后,在局部坐标系o6-x6y6z6中,光路按照从x6+向y6+转动,迎着光线(逆光)观察逆时针方向旋转,因此主光路经过M6镜之后旋转角度为+∆A,光路局部坐标系由o-xyz变为
,如图5所示。当俯仰轴旋转时,则天顶距Z变化,在∆t时间内,天顶距变化+∆D,迎着光线(逆光)观察俯仰轴逆时针旋转。入射光在M4镜发生折转,在局部坐标系o3-x3y3z3中即从x3+向y3−方向旋转,按照光线追迹推导,入射光经过M6镜之后,在局部坐标系o6-x6y6z6中,光路仍按照从x6+向y6−转动,迎着光线(逆光)观察顺时针方向旋转,因此主光路经过M6镜之后旋转角度为−∆Z,光路局部坐标系由
变为
。
在∆t时间内,望远镜入射光经过coude光路M6镜之后,由俯仰轴、方位轴旋转带来的角度变化为:
(11)
对上式求全微分,即:
(12)

Figure 5. Rotation schematic diagram of local coordinate system
图5. 局部坐标系旋转示意图
那么相应地,K镜旋转按照公式9所示的规则进行,则可消除2 m望远镜coude像面的视场旋转。
(13)
由图4所示的由光线追迹方法所建立的望远镜coude光路内各局部坐标系的关系,由于coude反射镜及K镜的引入,望远镜coude焦点处的成像位姿(o7-x7y7z7)较其实际位姿(o-xyz)旋转π/2。为了保证望远镜coude焦面成像位姿的准确性,需要旋转K镜方向角。按照第1节K镜光学传递矩阵理论可知,若像方沿光轴中心旋转角度π/2,则K镜相应的旋转π/4,可保证目标成像位姿不变,即coude焦面处的局部坐标系(o7-x7y7z7)与初始坐标系(o-xyz)重合。
如图6所示,此时局部坐标系与初始坐标系重合。K镜处于方向角−π/4时,其定义为2 m望远镜零位。
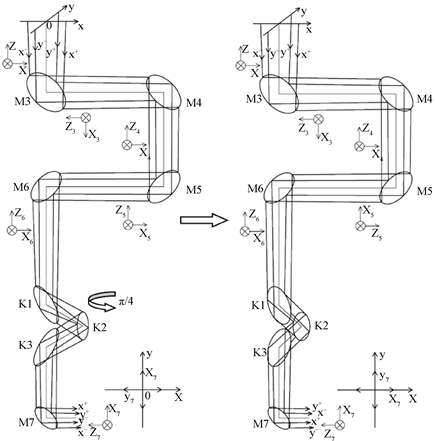
Figure 6. The ray tracing of coude path
图6. 望远镜coude光路光线追迹(K镜方向角旋转π/4)
4. 准直技术及误差分析
2 m望远镜在跟踪目标过程中,由于俯仰、方位轴的转动,光线在2 m库德光路中会相应的发生旋转,导致望远镜成像焦点处产生像旋。为避免库德焦点处的图像旋转,需要在2 m主光路中引入K镜系统。为保证K镜具有最好的消旋效果,必须要确保K镜光轴、K镜机械回转轴及2 m望远镜主光轴三轴重合,本节对K镜的准直技术及误差分析展开深入研究。
设望远镜主光轴为K1,K镜光轴为K2,K镜机械轴为K3,主光路经过K镜后的光轴为K4。在一般情况下,K1、K2、K3之间会存在位移或角度偏差,我们定义K1、K3轴之间的偏差为
,K2、K3轴之间的偏差为
,K1、K4轴之间的偏差为
,K镜机械轴旋转角度为
,那么根据公式3所推导的K镜光学传递矩阵可得如下关系:
(14)
主光轴经过K镜后的偏差
与K镜机械轴转动角度
在极坐标下的曲线形式如图7所示。
从曲线分析可知,当主光轴与K镜机械轴、K镜机械轴与K镜光轴存在偏差,旋转K镜机械轴时,主光轴经过K镜后会产生周期性变化的偏差量,由K镜传递矩阵原理可知,若K镜旋转1周,入射光旋转2周,因此由主光路与K镜机械轴的偏差
会形成2周封闭的曲线,而由K镜光轴与K镜机械轴的偏差
会导致2周曲线不重合,由图7(a)可知,偏差量最大值为
。而当消除K镜机械轴与K镜光轴之间的偏差,即
时,偏差曲线会形成2周重合的封闭曲线,偏差量最大值为
,如图7(b)所示。
 (a) ∆D1≠0,∆D2≠0
(a) ∆D1≠0,∆D2≠0  (b) ∆D1 ≠0,∆D2 =0
(b) ∆D1 ≠0,∆D2 =0
Figure 7. The alignment error curve of K mirror
图7. K镜准直误差曲线
根据误差曲线的规律性变化,我们设计如下准直装调策略:首先调整K镜内部反射镜K1、K3的倾斜,使误差曲线在0˚位置的误差点和180˚位置的误差点不断逼近,直至重合,此时K镜机械轴与K镜光轴偏差
。然后调整K镜整体平移及倾斜,使图7(b)所示的封闭的圆周曲线不断缩小,直至趋近至零点,则
。至此,
,主光轴K1、K镜光轴K2、K镜机械轴K3三轴重合。
为满足K镜系统的准直功能,K1、K3反射镜具备两维倾斜调整功能,K镜整体具备两维平移及两维倾斜的调整功能,如图8所示。

Figure 8. The mechanical structure of K mirror
图8. K镜系统结构
2 m望远镜K镜系统放置于M6镜与M7镜之间。在主光路中放置具有自调焦功能的测微准直望远镜(CZW),在K镜之后沿主光路分别放置2个CCD,用于记录主光路经过K镜后的位移轨迹,如图9、图10所示。

Figure 9. The sketch of alignment adjustment strategy
图9. K镜准直方案示意图

Figure 10. Alignment adjustable experiment of K mirror
图10. K镜准直实验测试

Figure 11. Light-spot recording in the process of alignment calibration (CCD2)
图11. K镜准直标定光点记录(CCD2)
按照既定设计的准直方案,具体的调整步骤为:旋转K镜,观察光轴经过K镜后在两块CCD上的运动轨迹点,并每转30˚进行计数,实验标定过程各个阶段如图11所示。在K镜机械轴旋转至0˚及180˚位置时,分别反复迭代调整调整K1、K3镜倾斜,使CCD1中的0˚点位置、CCD2中的180˚点位置不断向目标点逼近,如图11(a)所示。直至调整至图11(d)时,CCD所显示的误差曲线表明已消除K镜机械轴与K镜光轴之间的偏差,即
时。然后反复迭代调整K镜整体的平移及倾斜,使CCD1、CCD2中0˚及180˚位置的光点轨迹点不断逼近于零点。
由于K镜的轴系精度、气流扰动、机械晃动等一系列的影响,光点轨迹不可能完成重合于零点,准直标定最终状态如图11(f)所示。CCD2距离测微准直望远镜(CZW)距离约为
,光点轨迹最大偏移量为
,由此可计算最终的准直精度
约为:
(14)
5. 结论
本文针对国内某地平式望远镜coude焦面的像方视场旋转问题,在coude光路中引入消旋K镜装置,根据K镜光学传递矩阵,建立K镜消旋数学模型。利用光学追迹方法,推导望远镜coude光路中各局部坐标系的旋转及位置关系,从而得出望远镜K镜系统初始零位及其消旋策略。针对K镜的准直精度问题,根据其在旋转过程主光轴误差曲线的周期性变化特性,设计了基于帕斯卡窝线理论的准直装调方法,该方法将复杂的准直装调问题转化为关于帕斯卡窝线数学模型的参数修正问题,并建立了准直精度与装调参数的数学计算模型。通过装调过程不断修正误差曲线方程中的关键参数,使误差曲线不断趋近于最优值。本文所探讨的望远镜K镜消旋策略及其准直精度研究方法逻辑清晰,易于理解,其对带有coude光路系统的大型望远镜消像旋问题具有一定的研究意义及工程应用价值。
基金项目
吉林省科技发展计划优秀青年人才基金项目(20180520076JH)。