1. 引言
空气质量指数(AQI),就是根据环境空气质量标准和各项污染物对人体健康、生态、环境的影响,将常规监测的几种空气污染物浓度简化成为单一的概念性指数值形式,它将空气污染程度和空气质量状况分级表示,适合于表示城市的短期空气质量状况和变化趋势 [1] 。参与空气质量评价的主要污染物为细颗粒物、可吸入颗粒物、二氧化硫、二氧化氮、臭氧、一氧化碳等六项。
空气污染指数的取值范围定为0~500,其中0~50、51~100、101~200、201~300和大于300,分别对应国家空气质量标准中日均值的I级、II级、III级、IV级和V级标准的污染物浓度限定数值,在实际应用中,又把III级和IV级分为III(1)级、III(2)级和IV(1)级、IV(2)级。I级,空气质量评估为优,对人体健康无影响;II级,空气质量评估为良,对人体健康无显著影响;III级,为轻度污染,健康人群出现刺激症状;IV级,中度污染,健康人群普遍出现刺激症状;V级,严重污染,健康人群出现严重刺激症状 [2] ,见表1。

Table 1. AQI air quality classification
表1. AQI空气质量类别划分
本文获取了2018年山东省各市的空气质量状况数据(共5853条数据),基于R软件和SPSS软件运用CART分类树和径向基函数神经网络模型进行了建模,用2019年上半年的数据(共2335条数据)进行模型验证,比较两种模型的优劣。
2. CART树原理
2.1. CART树
分类与回归树模型(Classification and Regression Tree,简写为CART)由Breiman等人在1984年提出,是应用广泛的决策树学习方法。CART假设决策树是二叉树,内部结点特征的取值为“是”和“否”,左分支为“是”,右分支为“否”,等价于递归的二分每个特征,将输入空间即特征空间划分为有限个单元,并在这些单元上确定预测的概率分布,也就是在输入给定的条件下输出的条件概率分布。分类树的输出是样本的类别,回归树的输出是一个实数 [3] 。
2.2. 分类树
2.2.1. Gini指数
1) 假设有K个类,样本点属于第K类的概率为
,则概率分布的基尼指数定义为
(1)
2) 对于二类分类问题,若样本点属于第1个类的概率为p,则概率分布的基尼指数为
(2)
3) 对于给定的样本集合D,其基尼指数为
(3)
其中,
是D中属于第k类的样本子集,K是类的个数。
如果样本集合D根据特征A是否取某一可能值a被分割成
和
两部分,即
(4)
则在特征A的条件下,集合D的基尼指数为
(5)
表示经
分割后集合D的不确定性,基尼指数值越大,不确定性越大 [4] [5] 。
2.2.2. CART树算法
输入:训练数据集D,停止计算的条件;
输出:CART决策树。
1) 根据训练数据集D,从根结点开始,递归地对每个结点进行以下操作,构建二叉树:
2) 设结点的训练数据集为D,计算现有特征对该数据集的Gini系数。此时,对每一个特征A,对其可能取的每个值a,根据样本点对A = a的测试为“是”或“否”将D分割成
和
两部分,计算A = a时的Gini系数。
3) 在所有可能的特征A以及它们所有可能的切分点a中,选择Gini系数最小的特征及其对应的切分点作为最优特征与最优切分点。依最优特征与最优切分点,从现结点生成两个子结点,将训练数据集依特征分配到两个子结点中去。
4) 对两个子结点递归地调用步骤l~2,直至满足停止条件。
5) 生成CART决策树。
2.3. 剪枝
输入:CART算法生成的决策树
;
输出:最优决策树
1) 设
;
2) 自上而下地对各内部结点t计算
以及
;这里,
表示以t为根结点的子树,
是对训练数据的预测误差,
是
的叶节点个数;
3) 自上而下地访问内部结点t,如果有个
,进行剪枝,并对叶结点t以多数表决法决定其类,得到树T;
4) 设
;
5) 如果T不是由根节点单独构成的树,则回到步骤(4);
6) 采用交叉验证法在子树序列
中选择最优子树
[6] - [11] 。
3. 径向基神经网络
3.1. RBF神经网络
径向基(Radial Basis Function)网络是由Powell M.J.D.于1985年提出的,以函数逼近理论为基础构造的一类前向型网络,具有自学习、自组织和自适应等特点,相较于BP神经网络和灰色关联度,RBF神经网络具有学习速度快、精度高以及建立网络和训练网络时间少等优点。径向基函数网络是一个只有两层的网络,在中间层,它以对局部响应的径向基函数代替传统的全局响应的激发函数。由于局部相应的特性,它对函数的逼近是最优的,而且训练过程很短,它具有简单的结构、快速的训练过程及与初始权值无关的优良特性。
RBF神经网络的基本思想:用RBF作为隐单元的“基”构成隐藏层空间,隐藏层对输入矢量进行变换,将低维的模式输入数据变换到高维空间内,使得在低维空间内的线性不可分问题在高维空间内线性可分。就是用RBF的隐单元的“基”构成隐藏层空间,这样就可以将输入矢量直接(不通过权连接)映射到隐空间。当RBF的中心点确定以后,这种映射关系也就确定了。
3.2. RBF算法
采用径向基函数(RBF)神经网络,是具有单隐层的3层前向网络。
1) 输入层X:由信号源节点构成,仅起到数据信息的传递作用,对输入信息不作任何变换。
2) 隐藏层H:节点数视需要而定. 隐含层神经元核函数(作用函数)是高斯函数,对输入信息进行空间映射的变换。
3) 输出层Y:对输入模式作出响应. 输出层神经元的作用函数为线性函数,对隐含层神经元输出的信息进行线性加权后输出,作为整个神经网络的输出结果。
径向基神经网络的数学模型为
(6)
式中:x为神经网络输入的n维向量;
为输出层权重;
为径向基函数;
为径向基函数中心;
为宽度;b为输出层阈值;
为隐藏层神经元数目;
为向量
的范数,通常表示x与
间的距离。
通常选择高斯基函数为径向基函数,输出层阈值为0,该层神经元i的输出为
(7)
则隐藏层与输出层的映射关系为
(8)
式中:Y是输出向量,
,其中,q是输出层的单元数,W为输出层的权值,R为隐藏层神经元的输出值。
4. 描述性统计
首先对山东省2018年的空气质量数据进行了简单的描述性统计,得出2018年间各月份的空气污染状况。由图1可以看出,各月份空气质量类别为良的天数占的比重最大,其次为轻度污染,说明山东省整体的空气质量较为良好。各月份中出现空气质量类别为优的月份主要为七月、八月和九月,占比分别为25.2%、21.77%和12.29%,即山东省夏季的空气质量状况较好。各月份中出现严重污染的月份依次为一月、十一月和四月,占比分别为2.42%、1.25%和0.21%,各月份中出现重度污染的月份依次为一月、十一月、十二月等,占比分别为13.51%、9.17%和7.26%,即较为严重的空气污染主要集中在冬季和春季。
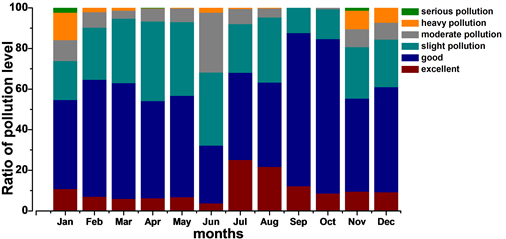
Figure 1. Air quality category for each month
图1. 各月份空气质量类别
5. 预测模型
5.1. CART决策树
5.1.1. 模型建立
空气质量预测模型的建立使用了空气质量等级作为最终的预测变量,该变量为离散型。选取PM2.5、PM10、SO2、NO2、O3_8h、CO,一共6个自变量进行预测模型的训练与测试,得到图2 CART树:
可以看到,训练之后,采用了PM2.5、O3_8h和PM10三个指标作为分支节点来建立决策树,而忽略了很多与AQI相关性不高的的特征。
上述决策树的分支过程如下:
首先,将PM2.5作为节点的第一特征,分为左支D1—
;右支D2—
;
对于D1,将O3_8h作为节点的第二特征,进一步分为左支C1—
;右支C2—
。对于D2,将PM2.5继续作为节点的第二特征,进一步划分为左支C1—
;右支C2—
。
如此进行下去,得到最终的CART树。
由上述CART树可以得出如下结论:
1) PM2.5、PM10和O3_8h是影响空气质量级别的主要因素。
2) 当
时空气质量级别直接划分为重度污染;
3)
,
或
时,空气质量级别划分为中度污染;
4)
或
,
或
,
,
时,空气质量级别划分为轻度污染;
5) 当
,
,
或
,
,
时,空气质量级别划分为良;
6) 当
,
,
时,空气质量级别划分为优。
5.1.2. 决策树的剪枝
剪枝是决策树学习算法解决模型“过拟合”的主要手段,在决策树学习中,为了尽可能正确分类训练样本,结合划分过程将不断重复,有时会造成决策树分支过多,这时就可能因训练样本拟合的准确度很高,以致于把训练集自身的一些特点当作所有数据都具有的一般性质而导致过拟合。因此,可通过主动去掉一些分支来降低过拟合的风险 [12] 。
建立树模型要权衡两方面问题,一个是要拟合得使分组后的变异较小,另一个是要防止过度拟合,而使模型的误差过大,前者的参数是CP,后者的参数是Xerror。CP是参数复杂度(complexity parameter)作为控制树规模的惩罚因子,简而言之,就是CP越大,树分裂规模(nsplit)越小。输出参数(rel error)指示了当前分类模型树与空树之间的平均偏差比值。Xerror为交叉验证误差,Xstd为交叉验证误差的标准差 [13] 。所以要在Xerror最小的情况下,也使CP尽量小。如果认为树模型过于复杂,我们需要对其进行修剪,下面列出了CP值与Xerror值。

Table 2. CART - tree complexity parameter table
表2. 决策树的复杂性参数表
由表2可以看出,可以看到,当nsplit为8的时候,即有四个叶子结点的树,要比nsplit为7,即八个叶子结点的树的交叉误差要小。而决策树剪枝的目的就是为了得到更小交叉误差(xerror)的树。因为本模型较为简单,所以不需要修剪。
5.1.3. 决策树的模型预测
从表3可以看出,模型的预测准确率为(1163 + 637 + 0 + 148 + 218 + 141)/2335 = 92.46%。
5.2. 径向基函数神经网络
5.2.1. 模型建立
在本模型中,训练集采用5853个样本,占总样本量的64%,测试集采用2335个样本,占总样本量的36%。RBF神经网络模型的输入参数和输入层的神经元数量根据实验因素确定,输出参数和输出层的神经元数量根据评价指标确定。在本文之中,输入参数为PM2.5、PM10、SO2、NO2、CO、O3_8h,输入层的神经元有6个,输出层的参数为优、良、轻度污染、中度污染、重度污染、严重污染,输出层的神经元有6个,隐藏层的隐藏函数为Softmax函数。建立如下图3:
5.2.2. 模型评价
ROC曲线指受试者工作特征曲线(Receiver Operating Characteristic Curve),是反映敏感性和特异性连续变量的综合指标,是用构图法揭示敏感性和特异性的相互关系,它通过将连续变量设定出多个不同的临界值,从而计算出一系列敏感性和特异性,再以敏感性为纵坐标、特异性为横坐标绘制成曲线,曲线下面积越大,诊断准确性越高。在ROC曲线上,最靠近坐标图左上方的点为敏感性和特异性均较高的临界值。
由上述ROC曲线图4可知,径向基神经网络模型对空气质量类别的拟合效果较好 [14] [15] [16] [17] [18] 。
由表4和表5可知,训练集的预测准确率为83.5%,测试集的预测准确率为84.2%,模型准确率相较于CART树模型的准确率不高。

Table 4. Confusion matrix of training set
表4. 训练集的混淆矩阵

Table 5. Confusion matrix of testing set
表5. 测试集的混淆矩阵
5.3. 模型优劣对比
CART树既可以做分类算法,也可以做回归。其优点为:1) 可以生成可以理解的规则。2) 计算量相对来说不是很大。3) 决策树可以清晰的显示哪些字段比较重要。缺点为:1) 当类别太多时,错误可能就会增加的比较快。2) 一般的算法分类的时候,只是根据一个字段来分类。
径向基神经网络的优点是:1) 分类能力好,学习过程收敛速度快。2) 具有唯一最佳逼近特性,且无局部极小问题存在。缺点是:RBF神经网络的非线性映射能力体现在隐层基函数上,而基函数的特性主要是由基函数的中心确定的,从数据点中任意选取中心构造出来的RBF神经网络的性能显然不能令人满意。
在上述对2018年1月至2019年6月的山东省空气质量类别预测的模型建立过程中可以看到,CART树模型的预测准确率为92.46%,而径向基函数神经网络模型的预测准确率为84.2%,显然,CART树模型的建立更有效。