1. 引言
采煤机牵引部在工作过程中主要负责采煤机的行走和牵引。两级行星齿轮机构作为牵引传动机构的重要组成部件,由于其传动比大、结构复杂,轮齿在啮合过程中存在内部激励,易产生较大的振动 [1] 。行星架作为行星齿轮传动的输出部分,在工作过程中易受到冲击、交变载荷的作用容易发生损坏,甚至断裂 [2] 。行星齿轮一旦出现故障,整个采煤机牵引部传动系统则会瘫痪,采煤机无法工作,煤矿将面临停产的威胁,给矿山企业带来巨大的经济损失。所以研究采煤机牵引部两级行星齿轮在工作过程中的各齿轮之间的啮合特性以及两级行星架在工作过程中的受载情况很有意义,目前的研究多是基于多刚体理论对行星减速机构进行动力学仿真分析,然后通过有限元方法分析行星架的静态受力情况 [3] [4] 。为了得到两级行星架在工作过程中的动载荷对其强度的影响,本文考虑两级行星架在仿真过程中的柔性变形,建立了采煤机牵引部两级行星齿轮系统的刚柔耦合动力学模型并进行仿真分析,得到两级行星齿轮传动系统在额定工况下两级级行星架的受力情况以及两级行星齿轮传动啮合的动态特性。
2. 刚柔耦合数学模型
考虑到两级行星减速器在工作过程中两级行星架所受扭矩较大,其弹性变形对行星齿轮啮合传动有一定影响,因此在仿真过程中必须同时考虑行星架的大范围运动和其本身的变形,以行星齿轮刚性构件所在的O-xyz为惯性坐标系,以二级行星齿轮架所在的O'-x'y'z'为柔性体局部坐标系。p为二级行星架上的一点 [5] ,图1为行星轮系刚柔耦合系统示意图,
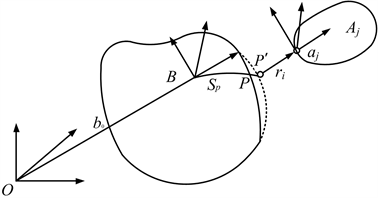
Figure 1. Sketch map of the rigid-flexible coupled system of the planetary gear train
图1. 行星轮系刚柔耦合系统示意图
二级行星架上任意一点p点的位置向量为:
(1)
式中,rp为p点在惯性坐标中的位置向量;up为变形模态矩阵Øp与广义坐标矩阵ξ的乘积;r为惯性坐标系原点到局部坐标系原点的位置矢量;A为欧拉变换矩阵;sp、up分别为p点在柔性坐标系中变形前的位置矢量及位移变化矢量。
对式(1)求导可得p点的速度为:
(2)
则二级行星架动能与势能的广义坐标形式为:
其中,M和K分别为广义质量矩阵和广义刚度矩阵,
为重力势能。将T、W以及能量损耗函数Γ代入式(3)的拉格朗日方程
(3)
中得到刚柔耦合多体系统的运动微分方程为:
(4)
式中,fg表示重力;D为模态阻尼矩阵;λ为拉格朗日乘子;ψ为约束方程;Q表为外部所施加的载荷。
3. 模型建立与动力学仿真
3.1. 刚柔耦合动力学模型建立
在三维软件UG中完成采煤机牵引部两级行星减速器中各零件的建模和装配,并将装配模型导入ADAMS软件中,建立了两级行星传动系统的多刚体仿真模型。
将两级行星架模型分别导入有限元软件ANSYS,并对行星架进行网格划分,完成两级行星架的柔性体模型后在ANSYS中分别输出两级行星架的模态中性文件(.mnf) [6] 。两级行星架的柔性体模型如图2和图3所示。

Figure 2. Flexible body model of the primary planet carrier
图2. 一级行星架柔性体模型

Figure 3. Flexible body model of the secondary planetary frame
图3. 二级行星架柔性体模型
在ADAMS中导入两级行星架柔性体文件,完成两级行星减速器刚柔耦合模型的建立。两级行星齿轮传动系统的刚柔耦合模型如图4所示。

Figure 4. Rigid-flexible coupled model of the two- stage planetary system
图4. 两级行星齿轮传动系统刚柔耦合模型
3.2. 约束与接触参数的施加
分别设置内齿圈相对地面为固定副、太阳轮和行星架相对内齿圈为旋转副、各级行星轮相对各级行星架为旋转副。
行星齿轮传动部分各齿轮间是通过接触传递力和运动的,分别在各齿轮之间添加接触。接触力分解成两部分:一部分是相互切入而产生的弹力,另一部分是由于相对运动产生的阻尼力 [7] ,其函数表达式为:
(5)
式中:x为两接触物体的初始距离,mm;
为两物体的相对速度,mm/s;x1为两物体之间的实际距离,mm;K为接触表面的刚度,N∙m−3/2;e为力的指数;c为两个物体表面接触过程中的阻尼系数,N/(s∙mm);d为接触表面的临界相互渗透量,mm。
根据赫兹接触理论可以求解两个变半径的柱体碰撞问题 [8] [9] ,齿面接触的法向力P与变形δ之间的关系为:
(6)
式中刚度K与接触体的材料和形状有关,其关系为:
(7)
式中:μ1、μ2分别为两种不同材料的泊松比;E1、E2分别为两种材料的弹性模量;R1、R2分别为接触点的半径,按分度圆的半径计算,式中“+”用于外啮合;“−”用于内啮合。通过式(7)计算得到行星齿轮机构各齿啮合刚度如表1所示。

Table 1. Meshing stiffness of gears in the planetary system
表1. 行星齿轮机构各齿啮合刚度
3.3. 驱动和负载的添加
采煤机牵引部牵引电机的额定功率为150 KW,电机在其额定功率下工作时,太阳轮的平均转速为1060˚/s、二级行星架输出的转矩为T1 = 116505 N/m,为了保证施加转速与转矩时传动系统能够平稳,利用STEP阶跃函数定义作用在虚拟样机上的驱动和负载扭矩,驱动添加在一级行星轮的太阳轮上:STEP (time, 0, 0, 0.02, −1060 d),负载添加在行星齿轮的二级行星架上:STEP (time, 0, 0, 0.02, 116505)。
4. 仿真结果及分析
4.1. 转速特性分析
根据行星齿轮传动比为:i1 = 4.235、i2 = 3.393,由此计算得到一级行星架转速n1 = 41.72 r/min,二级行星架转速n2 = 12.3 r/min。从图5可知仿真得到的太阳轮以及一二级行星架的角速度与理论值接近 [10] 。
4.2. 行星齿轮啮合频率分析
两级行星齿轮减速器中一级太阳轮的输入转率fs1 = 2.95 Hz。根据周转轮系传动比的计算法则,通过给整个轮系施加一个与行星架相反的转频−fc,将周转轮系转化为假想的定轴轮系 [11] ,则有:
(8)
式中,由于齿圈固定不动,因此其转频fr = 0;fs为太阳轮转频,Zr、Zs、Zp为齿圈、太阳轮、行星轮齿数。
行星齿轮啮合频率fm公式定义为:
(9)
代入数据则可以计算出第一级行星架的转频fc1 = 2.95 Hz,二级行星架的转频fc2 = 0.7 Hz。一级行星齿轮啮合频率为fm1 = 38.24 Hz、二级行星齿轮啮合频率fm2 = 13.73 Hz。
4.3. 行星齿轮啮合力分析
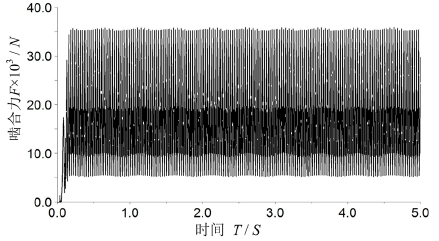
行星齿轮内部的运动是通过各齿轮之间的啮合来实现的ADAMS使用接触算法来实现齿轮啮合力的计算,通过后处理得到两级太阳轮啮合力曲线,如图6、图7所示。
 (a)
(a)  (b)
(b)  (c)
(c)  (d)
(d)
Figure 6. Graph of the engagement forces of the first-order solar wheel. (a) Graph of the engagement forces of the first-order solar wheel; (b) Graph of the engagement force in X direction of the first-order solar wheel; (c) Graph of the engagement force in Y direction of the first-order solar wheel; (d) Frequency spectrum of the engagement force of the first-order solar wheel.
图6. 一级太阳轮啮合力曲线。(a) 一级太阳轮啮合力曲线;(b) 一级太阳轮X向啮合力曲线;(c) 一级太阳轮Y向啮合力曲线;(d) 一级太阳轮啮合力频谱图。
 (a)
(a)  (b)
(b)  (c)
(c)  (d)
(d)
Figure 7. Graph of the engagement forces of the second-order solar wheel. (a) Graph of the engagement forces of the second-order solar wheel; (b) Graph of the engagement force in X direction of the second-order solar wheel; (c) Graph of the engagement force in Y direction of the second-order solar wheel; (d) Frequency spectrum of the engagement force of the second-order solar wheel
图7. 二级太阳轮啮合力曲线。(a) 二级太阳轮啮合力曲线;(b) 二级太阳轮X向啮合力曲线;(c) 二级太阳轮Y向啮合力曲线;(d) 二级太阳轮啮合力频谱图
通过仿真计算得出各级,从图6、图7可以看出各级齿轮啮合力在时域上的信号存在周期性变化的冲击幅值,这是由于齿轮啮合过程中时变啮合刚度引起的,在齿轮啮合力频域图上看出啮合力的响应频率成分由齿轮啮合基频、齿轮转频及其啮合倍频两侧以其转频为间隔的对称调制频率带。
4.4. 二级行星架受力分析
在ADAMS后处理分别输出两级行星架的应力云图,如图8所示。并在ADAMS后处理中获取二级行星架危险节点处应力时间历程如见图9所示。由工程图纸查的两级行星架的材料为30CrMoNi,材料的屈服强度为785 Mpa,取安全系数为1.859,则行星架的许用应力为422.3 Mpa。
从应力云图可以看出二级行星架上的应力值明显比一级行星架大,二级行星架最大应力为279 Mpa,没有超过其许用应力值。两级行星架的最大应力都主要集中在行星轮轴孔处以及行星架输出轴与前侧板的连接处,此处易产生应力集中为行星架的薄弱环节,在加工制造时应注意此处的加工工艺减小应力集中。
 (a)
(a) (b)
(b)
Figure 8. Stress contour of the two planet carriers. (a) Stress contour of the primary planet carrier; (b) Stress contour of the second planet carrier
图8. 两级行星架应力云图。(a) 一级行星架应力云图;(b) 二级行星架应力云图

Figure 9. Stress at the risk point of the second planet carrier
图9. 二级行星架危险点处应力时间历程
5. 结论
本文利用ADAMS和ANSYS软件建立了两级行星齿轮传动系统的刚柔耦合动力学模型,并对各级齿轮动态啮合力以及两级行星架受力进行仿真分析。仿真结果表明:
1) 由于齿轮啮合过程中啮合刚度的改变,各级齿轮啮合力存在着周期性变化的冲击力。啮合力在频域图上的频率成分由齿轮啮合基频、齿轮转频及其啮合倍频两侧以其转频为间隔对称的调制频率带。
2) 从两级行星架应力云图可以看出,二级行星架的应力值比一级行星架大,在工作过程中更容易损坏。
3) 两级行星架都在行星轮轴孔处以及行星架输出轴与前侧板的连接处存在应力集中现象,这些部位为行星架的薄弱环节。
本文研究结果不仅验证了行星齿轮啮合传动特性而且为二级行星架损坏机理及疲劳性能研究提供了依据。
项目资助
山西省煤机重点科技攻关项目(MJ2014-05-02)。
NOTES
*通讯作者。