1. 引言
食饵捕食者之间的动态关系一直是种群动力学模型的一个重要研究课题,众多学者对食饵捕食者系统进行研究并得到了大量的结论 [1] - [9]。人们在研究生物种群时着重关注种群的演变规律和对如何采取措施对种群进行合理的开发利用和保护的问题进行研究。针对这些问题的研究,除了可以对种群的变化和发展进行探索分析和加以估计,学者们还可以建立具有食饵收获率的捕食者–食饵模型,然后对该模型进行分析,得出需要多少的食饵收获率才能使该捕食者食饵模型系统达到一个动态平衡又可以满足人们的需求。因此研究具有收获率的捕食者食饵模型对生态保护和可持续发展具有重大意义,而众多学者针对此类模型已进行了广泛的研究。例如,文 [5] 研究了一类有常数收获率的Lotka-Volterra模型,着重分析了系统模型平衡点的存在性和稳定性以及极限环的存在性。文 [6] 研究了食饵带有收获率参数的Holling II型捕食者–食饵模型的Bogdanov-Takens分支,证明了该模型的Bogdanov-Takens分支是退化的。文 [7] 用线性化方法,分析了具齐次Neumann 边界条件的Holling第二类功能性反应捕食者–食饵模型的稳定性和Hopf分支,但此模型没有考虑捕食者对食饵收获率的影响,受到对具有常数收获率的捕食者食饵模型 [2] [3] [5] [6] 的启发,我们在本文当中也引入捕食者对食饵的常数收获率,即考虑食饵具有常数收获率和Holling第二类功能性反应的捕食者–食饵模型。首先给出系统模型平衡点的存在条件,然后主要讨论了平衡点的类型及稳定性和正平衡点的Hopf分支,且得出了产生Hopf分支的条件;最后,对该模型做了数值仿真模拟实验得到了相关结论。
相应的常微分模型如下:
(1)
其中:x为食饵种群的密度,y为捕食者种群的密度;
都是常数且为正;r表示猎物的内增
长率;k表示环境承载力;e表示相对损失;d表示捕食者的死亡率;h为捕食者对食饵的常数收获率。
表示捕食者的Holling II能反应。
首先对模型(1)作如下的变换
则可将模型(1)变为
(2)
其中:
,
,
。
2. 平衡点类型及正平衡点的稳定性
考虑到模型(1)的生物意义,所以我们之后的讨论都在
上进行。首先我们先考虑平衡点的存在性。令系统(2)右端为0,可得:
1) 若
,则有
(3)
记
。
a) 当
时,则系统(2)有唯一边界平衡点
。
b) 当
时,系统(2)有两个边界平衡点
和
。
2) 若
,则且当
且
时,系统(2)存在唯一的正平衡点
。其中,
, 。
。
接下来我们讨论平衡点的类型及其稳定性,系统(2)的Jacobi矩阵为:
(4)
1) 判断边界平衡点
的类型
将
代入Jacobi矩阵(4)中,可以得到系统(2)在
处的Jacobi矩阵为
利用文 [10] [11],通过计算,可得结论平衡点
为鞍结点。
2) 判断边界平衡点
和
的类型
将
和 代入Jacobi矩阵(4)中,可得到系统(2)在
和
处的Jacobi矩阵为
代入Jacobi矩阵(4)中,可得到系统(2)在
和
处的Jacobi矩阵为
利用文 [10] [11],通过计算,可得如下结论:
a) 若
,那么
为稳定结点;若
,则
为鞍点。
b) 若
,那么
为不稳定结点;若
,则
为鞍点。
3) 正平衡点
的稳定性
将 带入Jacobi矩阵(4)中,可以得到系统(2)在
处的Jacobi矩阵为
带入Jacobi矩阵(4)中,可以得到系统(2)在
处的Jacobi矩阵为
(5)
其中
。由于
若
,
;我们可得到系统(2)在正平衡点
处是局部渐近稳定的;
若
,
;我们可得到系统(2)在正平衡点
处是不稳定的。
令
,既有
,
;由参考文献 [12],则Jacobi矩阵
的特征方程有一对纯虚的特征根
(其中i为虚数单位,
)。
将
代入
中,解得
。
因此有如下结论:
定理1 当
且
条件成立时,
a) 若
,则系统(2)的正平衡点 是局部渐进稳定的;
是局部渐进稳定的;
b) 若
,则系统(2)的正平衡点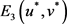 是不稳定的;
是不稳定的;
c) 若
,则系统(2)在正平衡点
处出现Hopf分支。
3. Hopf分支
由上一节讨论我们可以知道,当
且
时,系统(2)有唯一正平衡点
。其中
为初等焦点或者结点。下面我们讨论系统(2)在
附近的Hopf分支。
系统(2)在
处的雅可比矩阵为(5),其特征方程为
(6)
且当
时,Jacobi矩阵 的特征方程(6)有一对纯虚的特征根
。
的特征方程(6)有一对纯虚的特征根
。
我们取
为分支参数,设(6)的特征根为
,那么我们可以得到
,
。将
代入系统(2)的第一个方程可得:
记
,则有
,
。
由
解得
,且有
。
又
。于是有
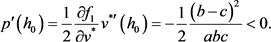
由
可知系统(2)满足产生Hopf分支的条件 [13]。因此系统(2)在
附近可产生Hopf分支。接下来我们来讨论产生的Hopf分支的方向。
令
,
。则系统(2)变成以下形式
(7)
因
,再作变换:
系统(7)变为
(8)
引入复变量: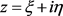 ,可以得到:
,可以得到:
其中:
把以上计算结果代入到一阶Lyapunov系数计算公式 [13]
我们可以得到
因此,根据文献 [13] 我们可以得到以下结论:
定理2 由
,
a) 当
时,模型(1)在
附近可以产生超临界的Hopf分支;
b) 当
时,模型(1)在
附近可以产生次临界的Hopf分支。
4. 仿真算例
由上一节定理2可知,若取
,
, ,
,则由于计算较为复杂,通过maple软件可计算得
,
,
,
,且我们可以算出
。那么系统(2)在
的时候就会有超临界Hopf分支产生。当
在大于
,
,则由于计算较为复杂,通过maple软件可计算得
,
,
,
,且我们可以算出
。那么系统(2)在
的时候就会有超临界Hopf分支产生。当
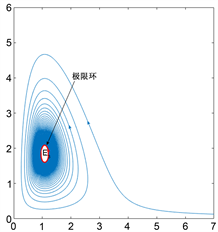
在大于 的附近取值时,在平衡点
附近则存在唯一的稳定极限环。如图1(a)所示。
的附近取值时,在平衡点
附近则存在唯一的稳定极限环。如图1(a)所示。
 (a)
(a)  (b)
(b)
Figure 1. (a) When
, there is a stable limit cycle near
; (b) When
, there is a unstable limit cycle near
图1. (a)当 时,在
附近存在一个稳定的极限环; (b)当
时,在
附近存在一个不稳定极限环
时,在
附近存在一个稳定的极限环; (b)当
时,在
附近存在一个不稳定极限环
若取
,
,
,
,则
,
,
,
,我们可以算出
。那么系统(2)就会在
处有次临界的Hopf分支产生。当
在小于
附近取值时,则在平衡点
附近存在唯一的不稳定极限环。如图1(b)所示。
5. 结论
文 [7] 用线性化方法,分析了具齐次Neumann边界条件的Holling II型捕食者–食饵模型的稳定性和Hopf分支。研究具有收获率的捕食者食饵模型对生态保护和可持续发展具有重大意义,因此本文对食饵种群进一步增加常数收获率后进行分析新的模型的平衡点类型及其稳定性和正平衡点的Hopf分支,即讨论了食饵种群具有常数收获率和Holling II型功能反应的捕食者–食饵模型的平衡点类型及其稳定性和正平衡点的Hopf分支问题且通过运用Matlab软件和Matcont软件做出了相应的Hopf分支图。由上面的讨论我们可以知道,超临界的Hopf分支可以产生稳定的极限环,其中的参数和初值是通过适当的选取来获得,最终使得捕食者和食饵的种群数量呈现周期性的变化而不消失。次临界的Hopf分支可以产生不稳定的极限环,其中的参数和初值是通过适当的选取来获得,当初值处在不稳定的极限环里面时,轨线趋向于正平衡点
,也就是说最终捕食者和食饵种群的数量趋于稳定而不消失
参考文献