1. 引言
肝硬化是一种由不同病因引起的慢性、进行性、弥漫性肝病,是各种慢性肝病发展的晚期阶段 [1]。全球范围内肝硬化死亡人数从1990年的80万人上升至2013年的120万人 [2],我国又是肝病的高发区。该病晚期易引起多种并发症,病情不可逆,治愈率低,死亡率高。目前临床采用肝穿刺取活检的传统方法诊断,但其对患者的创伤较大。近年来,建立在超声基础上的瞬时弹性成像技术 [3],吸引国内外专家目光,通过腹腔镜观察肝脏表面的形态来诊断肝硬化,但放置腹腔镜需要切开皮肤,将套管针刺入,患者将感到疼痛。如果能根据以往住院患者的病例资料准确地预测出患者是否发展到肝硬化,积极干预治疗,从而避免其他并发症的发生,对于提高患者的生存质量,延长患者的生命都有重要的价值 [4]。
随着科学技术迅猛发展,机器学习在医疗诊断领域得到广泛应用,例如:医学影像、药物挖掘、诊断预测等 [5] [6]。X光、CT (Computed Tomograph)和超声检查是获得医学图像的常用技术,然而,这三种技术所得的照片和图像皆受到计算机辅助诊断(Computer Aided Design)系统的性能构成限制。基于图像的CAD系统一般程序包括图像采集以及患者人口统计和临床属性、图像归一化、图像去噪预处理、病变检测和分割、特征提取和分类 [7] [8]。该程序涉及大量计算步骤,十分繁琐;此外,不相关的特征和不准确的分割可能导致预测模型的结果不精确 [9]。一些研究报告显示选取适合的生物标记物可作为其代替方法。因此,本文实验使用人体测量学和常规血液分析结果组成的数据库。
国内外学者将神经网络、逻辑回归和支持向量机等方法应用于疾病诊断预测中,并且将上述传统的单一分类器改进以提高整体的诊断率。然而,在多数情况下,集成分类器的效果胜过单一分类器。随机森林是最强大的集成方法之一,它在机器学习和数据挖掘中具有广泛应用,特别是对于大型高维数据的分类。RF (Random Forest)算法通过创建一组未修剪的决策树来维持训练数据集的低偏差。但是,随机森林存在一些不足:对于有不同取值属性的数据,取值划分较多的属性会对随机森林产生更大的影响;当训练数据噪声比较大时,容易产生过拟合现象;由于其本身的复杂性,RF比其他类似的算法需要更多的时间来训练。对此,文献 [10] 提出了一种通过向森林添加新树来迭代地执行增强的用于分类任务的强化准随机森林,为每个属性分配权值,并识别导致训练期间出现错误分类的数据点对应属性,但却有运算时间较长的缺陷。为了解决数据冗余和噪声问题,文献 [11] 提出了基于集合–边缘的随机森林方法,该方法将RF与计算集合边缘值相结合,产生一种新的子采样迭代技术。为了提高癌症存活性预测的准确率,文献 [12] 提出基于遗传算法对随机森林(Genetic Algorithm-Random Forest)改进的集成分类算法。通过大量实验表明:此方法具有更高的运算效率和准确的预测结果。与此同时,还可以降低医疗成本、节约医疗资源、减少患者疼痛。以上文献所提出的方法尽管能弥补随机森林的不足,但却忽略RF使用随机因子来控制森林中树木之间多样性这一特点。
多样性对RF的性能有重要影响,其泛化误差体现在单树的强度和树的依赖性两个方面。鉴于此,本文提出一种基于多视图理论新方法,在随机森林中增加视图并减小深度方法,以减少树木的大小并增加森林中的树木数量。该方法使用多视图方法,能够采用多个本地视图执行对象识别任务。并且使用人体测量学和临床属性组成的数据库,对肝硬化疾病进行更准确的诊断预测。
2. 随机森林Random Forest
2.1. Bagging
Bagging是一种通过使用其他数据来控制方差从而改进预测任务的方法。它通过从输入数据中随机选择n个样本来工作。样本大小与输入数据大小相同。但是,这n个样本使用替换策略,因此选择样本的
概率为
。在选择每个大小为n的p个样本集之后,它为每个样本集训练回归器/分类器 [13]。预测结果由分类器中的多数投票方案获得。Bagging通过调整数据的方差来改善泛化误差。它使得噪声数据的选择极不可能,从而减少其对假设的影响。
2.2. Random Forest构建过程
随机森林是一种常用的集成学习算法,其采用随机方式建立一片树林,森林中包含众多有较高预测精度且弱相关的决策树,并形成组合预测模型。每棵树随机选择观测与变量进行分类器构建,最终结果通过投票得到。一般每棵树选择logN个特征(其中N为特征数),如果每棵树都选择全部特征,则此时的随机森林可以看成是bagging算法。随机森林算法的流程图如图1所示。
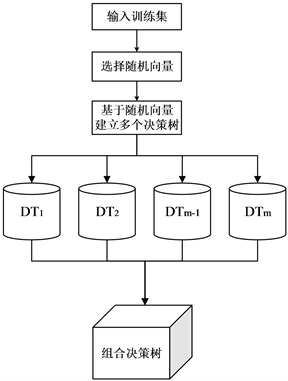
Figure 1. Random forest algorithm block diagram
图1. 随机森林算法原理框图
3. 增加视图并减小深度的随机森林
与Breiman提出的集合方法相类似 [14],根据所谓的“基础学习者”
的集合构建了一个集合预测器f。在回归中,f为基础学习者的平均,J为基础学习者总数。
(1)
在分类中,
是最常被预测的类,即投票过程。
(2)
(3)
在RF算法中,第j个基础学习器是由
表示的树,其中
是随机变量的集合,
是服从均匀分布的随机数。欲增加视图数量和减少树木深度,在算法中引入深度限制参数,从而限制RF树中的级别数。算法1显示了深度有界随机森林(Depth Bounded Random Forest)方法,该方法的提出基于文献 [15] [16] 中的RF算法。在标准RF中,树木在没有修剪的情况下生长,而DBRF算法中树的深度受l限制。
算法1:深度有界随机森林(DBRF)算法
输入:训练集
,
输出:边界深度为l的随机森林
Step1For l = 1 to特征的数量
Step2For j = 1 to J
Step3从训练集D中提取一个大小为n的Dj作为引导子样本
Step4使用引导子样本Dj作为训练数据,使用Depth Bounded Binary Recursive Partitioning拟合树
Step5从单个节点的所有观察值开始
Step6对于深度小于l的每个未分割节点,以递归方式重复以下步骤:
Step7从p个可用预测变量中随机选择m个预测变量
Step8在步骤(6)的m个预测变量上找到所有二进制分裂中的最佳二进制分裂
Step9使用步骤(7),将节点拆分为两个后代节点
Step10结束Forj循环
Step11在新点x进行预测,使用公式(2)计算f(x)。hj(x)则使用第j个树预测x处的响应变量
Step12计算RF的预测精度,直至达到终止条件,停止FOR循环
构造的深度有界树与全深度树类似,因为它将具有混和标记数据的叶节点或属于特定类的数据的叶节点,因此可以类似于标准RF执行分类计算。此外,算法1中的深度参数l可以设置任何所需的值,包括特征向量中的最大特征数。
DBRF算法中的第四步使用深度有界二进制递归分区(Depth Bounded Binary Recursive Partitioning)算法(算法2)来构造深度有界树。DBBRP算法类似于原始的二进制递归分区算法 [15],具体过程如下:
算法2:深度有界二进制递归分区(DBBRP)算法
输入:
表示训练数据,
和深度l
输出:结果树
Step1从单个节点中的所有观测值
开始
Step2对于深度低于l的每个未分割节点,以递归方式重复以下步骤:
Step3在所有p个预测变量上的所有二进制分裂中找到最佳二进制分割
Step4使用最佳拆分(步骤3)将节点拆分为两个后代节点
Step5对于x处的预测,将x向下传递到树中,直到它落在终端节点中
通过增加视图数量使得在RF中添加尽可能多的树并同时通过限制树的深度来限制在每个树中评估的特征数量来完成。因此,每个样本树的大小将远小于在标准RF中构建和评估树木。这样有三个好处:
No 1. 每棵树的RF学习速度增加。
No 2. 存储在存储器中的树的大小要比标准RF树小得多。
No 3. 评估更多的视图可以减少错过重要特征的机率,从而提高准确性和可靠性分类器。
4. 实验结果及分析
为了评估提出的方法的性能,在数据集上实现该方法并进行测试。
4.1. 样本组成
本文实验采用某地肝病患者真实数据集,其中包含167个非肝脏患者记录和416个肝脏患者记录,分组的类别标签:0未患肝硬化、1患肝硬化(如图2);数据集包含441个男性患者记录和142个女性患者记录(如图3)。
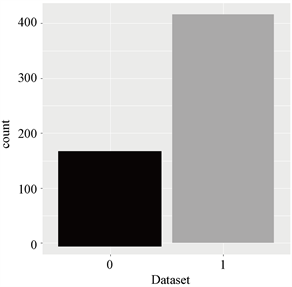
Figure 2. No disease and number of patients
图2. 未患病与患病人数
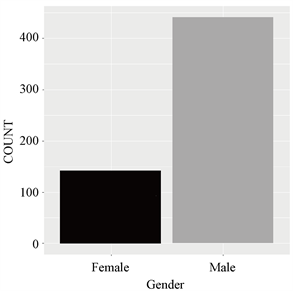
Figure 3. Number of sick men and women
图3. 患病男性与女性人数
数据集由583位志愿者的常规血液分析与人体测量结果组成,涉及9个变量,即生成583 × 9的数字向量组。属性见表1。

Table 1. Dataset attribute information
表1. 数据集属性信息
4.2. 数据分析
从表1发现,常规血液分析中存在一些名称相类似的属性,如:总胆红素与直接胆红素、谷丙转氨酶与谷草转氨酶、总蛋白质与白蛋白。为了更直观地看出他们之间的关系,本文通过散点图对其进行线性拟合,如图4。
通过观察图4可知:总胆红素与直接胆红素的数值线性相关,而谷丙转氨酶与谷草转氨酶、总蛋白质与白蛋白不存在线性关系。另外,对于变量的选择如图5所示,则使用热图并以矩阵形式呈现,判断变量之间的相关性。
该热图以矩阵形式表达变量的相关性,其中矩阵每个元素是皮尔逊相关系数且范围[−1, 1],用于计算横向两个连续性随机变量间的相关系数。该数据集中的总胆红素、谷丙转氨酶和白蛋白这三个变量彼此高度相关,因此对其降低处理。
4.3. 深度对分类准确性的影响
图6展示在肝硬化数据集上,深度对于分类精度的影响,体现出深度对分类准确率的重要性。通过观察图6:当深度达到5时,再增加树的深度不会对分类准确率产生显著影响。也就是说,分类精度在一定深度之后有界并且在不降低分类精度的情况下可以限制深度。所以,本实验的深度设置为5。
4.4. 森林中树木数量对分类准确性的影响
下面实验旨在表明相当于多视图理论中的视图数的树木数量的重要性。首先使用能够体现随机森林泛化能力的袋外(Out-Of-Bag)样本来计算错分类比例。对于OOB样本来说,森林中每一颗不经其训练的树给出各自独立的分类结果,即让它们分别投票。在最终分类时,森林选择得票最多的分类结果作为肝硬化诊断的总体输出。如图7所示,OOB错误率随着森林规模的增加而趋于稳定。当决策树数量达到130后,错判率基本保持稳定。故,在本次肝硬化诊断实验中参数ntree可设置为130。
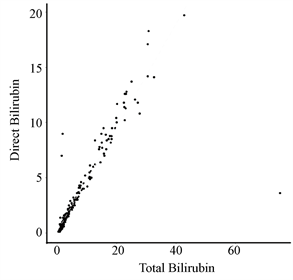
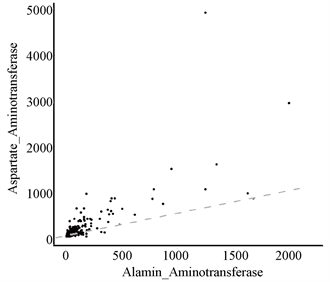
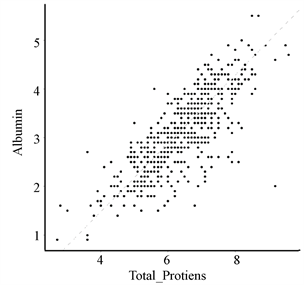
Figure 4. Scatter plots of Total_Bilirubin & Direct_Bilirubin, Alamine_Aminotransferase & Aspartate_Aminotransferase, Total_Protiens & Albumin
图4. 总胆红素与直接胆红素、谷丙转氨酶与谷草转氨酶、总蛋白质与白蛋白的散点图
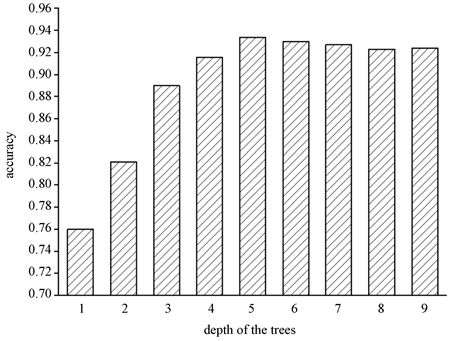
Figure 6. Classification accuracy corresponding to different depths in random forestst
图6. 随机森林中不同深度对应的分类准确率
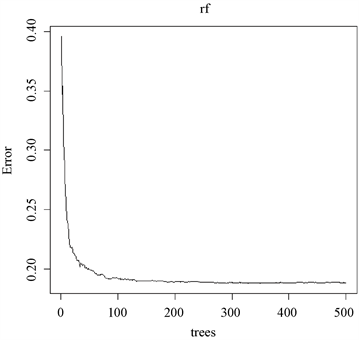
Figure 7. Relationship between OOB error rate and number of decision trees
图7. OOB错判率和决策树数量的关系
由于随机森林在节点划分时选择的不是全部特征,而只用到了它的一个子集,接下来本文将对肝硬化数据中的每一个特征在分类时起到的作用进行首先排序。首先,在训练随机森林你和过程中记录每个数据样本OOB错误,并在森林中求平均值。训练完成后,令树重新选择特征,再计算所有树新的OOB错误率。随之产生的标准差规范化得分可以用于衡量特征的重要程度,见图8。
由图8可知,从对输出变量预测精度影响来看(左图),直接胆红素、谷草转氨酶、碱性磷酸酶较为重要。从对输出变量异质性下降程度影响的角度观察(右图),谷草转氨酶、碱性磷酸酶、年龄较为重要,即通过血常规检测的谷草转氨酶数值、碱性磷酸酶数值、不同年龄的人群,对判断是否罹患肝硬化疾病具有重要影响。
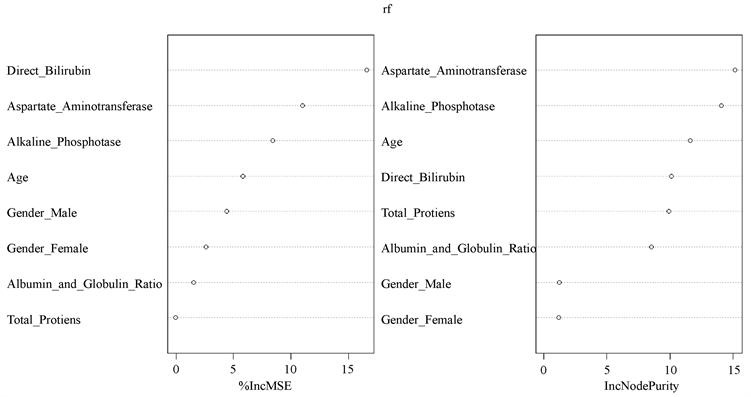
Figure 8. Visualization graph for input variable importance measures
图8. 输入变量重要性测度的可视化图形
4.5. 与其他分类器对比
上述数据集将在原始随机森林、改进后的随机森林、神经网络和逻辑回归四种分类器上实现。采用accuracy准确率作为评价指标 [17]。
(5)
其中四个参数的说明:True Positive:预测为正例,实际为正例;False Positive:预测为正例,实际为负例;True Negative:预测为负例,实际为负例;False Negative:预测为负例,实际为正例。
由图9可知:TP和TN表示预测正确,FP和FN代表预测错误。accuracy计算的是正确预测的样本数占总预测样本数的比值,它不考虑预测的样本是正例还是负例,其考虑的是全部样本。
在图10很直观地看出:本文提出的深度有界随机森林算法比原始随机森林的分类准确率提高3.76%。相比之下,逻辑回归的准确率较低,为73.37%,而神经网络的表现欠佳,准确率仅为62.71%。可以看出增加视图减少深度的随机森林的准确率最高。
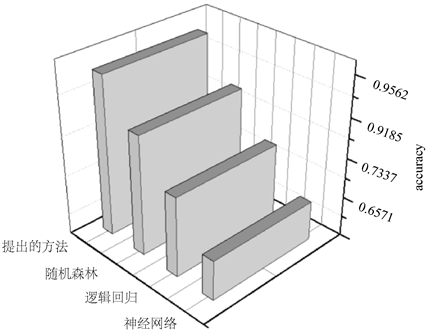
Figure 10. Accuracy of running four classifiers
图10. 运行四种分类器的准确率
5. 结语
本文以限制树木深度、减小树木大小为主要思想,提出一种新的随机森林算法。所提出的深度有界随机森林算法构建更多的随机森林深度较少的树木。不同于以往图片数据,本文采用人体测量学组成的数据集进行实验,结果表明与原始RF相比,本文提出的限制深度的RF具有更高的准确率。进一步的工作将尝试当数据数量增大时对于准确率的影响以及使用更丰富的评价指标。
基金项目
黑龙江省教育厅基本业务专项理工面上项目(135209234);齐齐哈尔市基金项目(GYGG-201913)。
NOTES
*通讯作者。