1. 引言
随着科学研究的推进,小波理论体系不仅可以定义在实数域上,还可以定义在其他域上,比如阿贝尔群、分层树、一些分形集等 [1] [2] [3] [4]。
近年来,小波与分形的结合已经成为科学研究的热点问题。小波分析技术可以有效地揭示分形局域标度性质,小波分析还具有放大和移位的功能,它是从远处到近处观察形体,这与分形的本质是尺度变化相类似。Mallat和Meyer建立的多分辨分析(Multi-Resolution Analysis, MRA)为小波分析奠定了基础,多分辨分析与分形之间也有一定的联系。多分辨分析是从远到近观察形体,先观察其轮廓,再观察其线条,进一步观察物体的细节纹理,这体现了从低分辨到高分辨的思想,对具有自相似性质的分形的观察也是这样,通过从大到小的不同尺度变换,在越来越小的尺度上观察越来越丰富的细节,这也是从低分辨到高分辨的观察过程。
多分辨分析是由S. Mallat引入的。他在空间概念上形象的说明了小波的多分辨特性。1989年,Mallat在探究小波变换多分辨分析理论与图像处理的应用时,受到塔式算法的启发,提出了信号的塔式多分辨分析分解与重构的快速算法,即著名的Mallat算法。MRA形成了构造正交小波基的一个框架,比如常用的Daubechies紧支撑正交小波基可以看作是该框架下的产物 [5]。
D. Dutkay和P. Jorgensen介绍了由迭代仿射函数系统产生的分形的扩张和平移所生成的
有限测度空间上的多分辨分析的概念 [6],但主要是基于一维分形集的情形,比如一维康托尔集上的多分辨分析。本文讨论了基于Sierpinski垫上的多分辨分析,证明了基于Sierpinski垫的膨胀分形集上的多分辨分析,丰富了多分辨分析的内涵。
2. 预备知识
在本文中,用R表示实数集合,Z表示所有整数集合,
表示复数空间。下面先讨论多分辨分析的定义。
定义1 [6] 空间
中一列闭子空间
称为
的一个依尺度函数
的多分辨分析,如果该序列满足下列条件:
(1) 嵌套性:
(2) 逼近性:
,
(3) 伸缩性:
(4) 平移不变性:
(5) Riesz基存在性:
存在函数
,使得
构成
的一个Riesz基,即函数序列
线性无关,且存在常数A和B,满足
,使得对任意的
,总存在序列
使得
且
,则称
为尺度函数,并称
生成
的一个多
分辨分析
。
特别地,若
构成
的一个标准正交基,则称
为正交尺度函数;相应地,称
生成
的一个正交多分辨分析
。
由一维多分辨分析的张量积空间构造二维多分辨分析,我们给出如下定义:
定义2 [7] [8]
1. 用
表示平面上的平方可积函数空间,即
设
和
是由尺度函数
和
生成的两个多分辨分析,则可以得到
和
的张量积
空间
。由于
的基底为
,
的基底为
,所以
的基底为
。对于二元函数 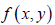 ,引入记号
,记
,则
是
的基底。
,引入记号
,记
,则
是
的基底。
这样,
就形成
中的一个多分辨分析, 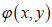 就是相应的尺度函数。
就是相应的尺度函数。
2. 在
函数空间的一串子空间序列集合
称为依尺度函数
的多分辨分析:
(1) 嵌套性:
(2) 逼近性:
,
(3) 伸缩性:
(4) 平移不变性:
(5) 规范正交基:
, 是
的一组标准正交基。
是
的一组标准正交基。
令
是
在
中的正交补空间,
构成
的基底,则由多分辨分析可以得到两个结果:
3. Sierpinski垫上的多分辨分析
给定平面
上的一个单位正三角形
,在每边上取中点,然后两两连结,构成四个边长为1/2的正三角形,把中间的三角形去掉(但是保留其三条边),得到集合
(见图1),然后在
的三个三角形的每边取中点,分别连结成边长为1/22的小正三角形,又分别去掉中间一个(同样保留每个三角形的三边),剩下一共有32个三角形。如此不断继续下去,得到一个平面集列: 可见
是由
个边长为1/2k的正三角形组成。
的极限集
称为Sierpinski (谢尔宾斯基)垫片,它是一个著名的分形集 [9] [10]。
可见
是由
个边长为1/2k的正三角形组成。
的极限集
称为Sierpinski (谢尔宾斯基)垫片,它是一个著名的分形集 [9] [10]。
的总面积为
,所以当
时,S的面积等于如下极限:
。
我们将原三角形
视为
空间中的子空间
,把每次去掉的部分子空间记为
,将余下的部分记为
(如图2)。
容易看出任意两个不同区域的交集是空集,表示它们的特征函数(该区域的元素集合)
与
彼此正交,简记为
,则有
,
,
。
 S0 S1S2S3S
S0 S1S2S3S
Figure 1. Establishment of Sierpinski gasket
图1. Sierpinski垫的形成过程

Figure 2. MRA of Sierpinski gasket
图2. Sierpinski垫上的多分辨分析
我们发现
与
互不相交,说明分别定义在
与
上面的特征函数彼此正交,对于不同的子空间
与 ,它们之间彼此正交,即定义在它们上面的特征函数彼此正交。然而对于不同的子空间
与
,并不是正交的,我们有
,
是
在
中的正交补空间,依此类推,
,
,因此,
,它们之间彼此正交,即定义在它们上面的特征函数彼此正交。然而对于不同的子空间
与
,并不是正交的,我们有
,
是
在
中的正交补空间,依此类推,
,
,因此, 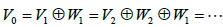
在V上定义尺度函数
,W上定义小波函数
。将
上的基函数
和
上的基函数
结合起来展开 空间中的信号
,
空间的正交分解为
。相应的信号
的分解过程为
空间中的信号
,
空间的正交分解为
。相应的信号
的分解过程为
我们对  空间赋予多分辨分析的几何特征,将多分辨分析这一抽象的数学定义与实用信号结合起来。
空间赋予多分辨分析的几何特征,将多分辨分析这一抽象的数学定义与实用信号结合起来。
4. 基于Sierpinski垫的膨胀分形集上的多分辨分析
4.1. 定义直角三角形Sierpinski垫
特别地,我们旨在于研究直角三角形Sierpinski垫。
在
上构建一个直角三角形
,顶点分别是
.设对角扩张矩阵
,令
其中,
,则
继续归纳下去,有
因此,我们可以得到
上的紧子集的一个嵌套序列
。
然后,定义Sierpinski垫分形
(见图3),这个Sierpinski垫S满足自相似关系
我们知道S的Hausdorff维数是
,记
表示在S上的s维Hausdorff测度,简记为
,则  。更一般地,如果E是S的一个Borel子集,则
。
。更一般地,如果E是S的一个Borel子集,则
。
4.2. 基于Sierpinski垫的膨胀分形集上的多分辨分析
定义一个与Sierpinski垫S有关的一个膨胀分形集
对于
的每一个Borel子集E,测度满足
 .
.
在Hilbert空间
上,构建酉扩张算子D和酉算子T,定义如下:
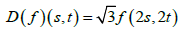 (1)
(1)
. (2)
这些算子满足一个标准的交换关系:
定理1
设D和
是上述定义的酉算子,则
证明:由(1)式和(2)式可得:
所以
现在构建一个
上的多分辨分析。定义一个闭子空间
,
,
其中
是Sierpinski垫三角形上的特征函数(对应标准多分辨分析中的尺度函数)。Sierpinski垫S满足自相似关系
在测度为0的集合上,上述的并集是互相非交的并集,且它的特征函数
满足扩张方程
通过构造,
在算子
下是不变量。对于每个
,定义
可以看出
因此,
。由此看出,闭子空间
形成了
的闭空间的一个递增的嵌套序列。
下面证明子空间
形成一个多分辨分析
定理2
设
是上述构造的
的子空间,设D, 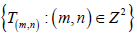 是定理1中的酉算子,则有
是定理1中的酉算子,则有
(1)
(2)
(3)
(4)
证明:
(1) 由Sierpinski垫S的自相似关系和对应的扩张方程可知,因为
又因为
则
所以
即
(2) 因为
所以
(3) 我们将证明对于任意Hausdorff可测子集
,其中
,则
含于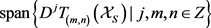 的闭包中。
的闭包中。
因为
,我们可以写一个集合
,其中
。
容易证明,每个集合
的特征函数含于
的闭包。因此,通过扩张和平移,不失一般性,我们可以假定任意可测集
。
设
是S中所有子三角形的左下顶点的集合,对于每一个
,有一个递减的交集:
,
其中
是S的一个平移的n次扩张。我们可以得到
。由测度的次
可数可加性得,
。
令
,则
。因为S是一个度量空间,所以
也是,尽管
不再是闭的。
因此,不失一般性,我们假定
,令
是由
的子Sierpinski垫组成的,它是
的子集的一个半代数,也就是说,
中元素的有限非交的并形成了
子集的一个代数。我们用
表示这个代数,在
上作用一个Hausdorff测度,得到一个
上的集值函数,记为
,它满足Caratheodory扩张定理的条件。因此,
可以延伸为
的所有子集的一个外测度,
与代数
上的Hausdorff测度
一致。因此,
决定了可测集上的一个
代数
,这个可测集含有包含
的最小的
代数
。如果将外测度
限制到
上,则变成测度,记为u,显然
是一个完备的测度空间。而且,因为  是有限的,由Caratheodory扩张定理可知,将
上的
延伸成含有
的最小的
代数是唯一的。因此,不论在
上还是
上,都有
。剩下的问题是,当构造
是有限的,由Caratheodory扩张定理可知,将
上的
延伸成含有
的最小的
代数是唯一的。因此,不论在
上还是
上,都有
。剩下的问题是,当构造 子集上的外Hausdorff测度时所产生的
代数是否大于利用Caradiodory扩张定理产生的Hausdorff测度
的
代数
?
子集上的外Hausdorff测度时所产生的
代数是否大于利用Caradiodory扩张定理产生的Hausdorff测度
的
代数
?
注意,集合
族除了是
子集的半代数外,也是
的任意子集的一个Vitali覆盖,也就是说,对于每一个
和每个
,都有一个子集
,其中
。利用Vitali覆盖上的Caratheodory扩张定理构造的外测度是度量外测度,因此,对于任意子集A和B,其中
,满足
。此外,如果
是度量空间X上的度量外测度,则该外测度下的可测集的
代数包含X的Borel集的
代数。我们将这个结果应用于
可以推导出
是度量外测度,且
包含
的Borel集。因此,由
构造的
可测集的
代数包含
的Borel集以及
的开集和闭集。因此,在S的Borel子集上,
与u是一致的 [11]。
最后,如果利用Caratheodory扩张定理在集合X上用代数
构造有限测度u,则给定任意可测集
,存在
的一个元R,使得
。
由上述结果以及
的可测子集E可知,存在一个
集
,其中
。因
为在
的Borel集的
代数上,
,
,则可推导出存在一个有限集Sierpinski子三角形
,其中
。但是,因为
,所以
。因此,
含于
的闭包 [12] [13] [14]。
(4) 对于
,如果
,则对于每一个
,存在一些
,使得
。
对于使
成立的足够大的j,有
,且对于这些j,
是
常量。因此,
一定是
,
,
之一。因为
一
定是
上的常量,所以每个并是嵌套的意味着f在这些并上都是常量.因为每个并的测度是无限的,所以这些常量必须都是0 [15]。
因此,
构成了
上的一个多分辨分析,
构成了
的标准正交基。
5. 结束语
由于小波分析可以同时在时域和频域内进行局部化信号,并对信号在不同尺度上进行分解和重构,所以研究分形集上的多分辨分析具有重要的现实意义,为分形集上的小波变换奠定基础。本文首先讨论了基于Sierpinski垫上的多分辨分析,然后通过构建酉扩张算子D和酉算子T,结合分形几何中的测度知识证明了基于Sierpinski垫的膨胀分形集上的多分辨分析。