试析网上常见的一个E = Mc²推导过程中的错误

An Analysis for the Error of a Common Derivation Process of E = Mc² on the Internet

摘要: 用工程计算软件MATLAB详细分析验算了网上流传较广的一个E = Mc²的推导过程，结果表明在正确使用现有数学工具的前提下，该过程不可能推导出E = Mc²。介绍了基于量纲分析，从物理和数学角度推导E = Mc²的方法，该方法与相对论无关。

Abstract: A derivation process of E = Mc², which is widely spread on the internet, is checked in detail by the engineering calculation software MATLAB. The results show that it is impossible to deduce E = Mc² by using existing mathematical tools correctly. This paper introduces the method of deducing E = Mc² from physical and mathematical point of view based on dimensional analysis, which is independent of relativity.

1. 引言

E = Mc²是一个著名的公式(其中，E为能量，M为质量，c为光速)，在(狭义)相对论中称为质量–能量关系式，或者称为质能方程，它是相对论的基础之一。一个源自国外出版物的基于微积分推导E = Mc²的计算过程在网上流传较广。作者用MATLAB对该计算过程逐步进行了详细分析和验算，结果表明在正确使用现有数学工具的前提下，该过程不可能推导出E = Mc²。可以基于量纲分析方法，从物理和数学角度推导E = Mc²，该方法与相对论无关。

2. 用MATLAB验算网上常见的一个推导E = Mc²过程

网上常见的一个推导E = Mc²的过程如图1所示 [1]。限于条件，作者未能查到其原始出处，这里只是转引。

Figure 1. A common derivation process of E = Mc² on the internet

图1. 网上常见的一个推导E = Mc²过程

在函数记号 $y=f\left(x\right)$ 中，x称为自变量，y称为因变量。定积分的一般形式为 ${\displaystyle \underset{a}{\overset{b}{\int }}f\left(x\right)\text{d}x}$，式中积分下限a和积分上限b均为常数，即 ${\displaystyle \underset{a}{\overset{b}{\int }}f\left(x\right)\text{d}x}$ 为固定积分限的积分。积分号里面dx之外的部分称为被积函数。如果积分限是变化的，则称为变限积分；变限可以是只变一个积分限，例如 ${\displaystyle \underset{0}{\overset{\sin t}{\int }}\frac{\sin x}{x}\text{d}x}$ 等；也可以是两个积分限同时变化，例如 $$ 等。变限积分还有一种比较特殊的形式，即以被积函数f(x)的自变量x作为积分的上限或者下限，例如 $$ 等。

MATLAB是一款功能强大的工程计算软件，是科学技术领域应用和影响最广泛的三个计算机数学语言之一。利用MATLAB的符号运算工具箱，可以直接求解一般的微积分计算问题。当然MATLAB不是万能的，对于某些特殊的微积分问题，MATLAB同样无能为力。

$y=f\left(x\right)$ 的微分定义为 [2]

$\text{d}y=f^{\prime }\left(x\right)\text{d}x$ (1)

式中 $f^{\prime }\left(x\right)$ 为一阶导数。进一步取 $f^{\prime }\left(x\right)$ 的导数可以得到二阶、三阶及高阶导数。在MATLAB中，如果函数及自变量已知且均为符号变量，可以用diff( )命令求解给定函数的各阶导数。

具体到图1中的(F)环节，这里用圆括号( )代替图1中的○，记

$y=y\left(v\right)=\frac{m_{0}v}{\sqrt{1-{\left(v/c\right)}^2}}$ (2)

这里为了便于比较，式(2)与图1中的记号对应一致，有关符号均未使用斜体。

在MATLAB中输入下列语句

>> syms m0 c v;

>> simple(diff((m0*v)/sqrt(1-(v/c)^2),v))

simple( )为MATLAB的化简命令。化简后的最终结果为

ans =m0/(-(-c^2+v^2)/c^2)^(3/2)

将上述结果写成解析形式，即有

$y^{\prime }\left(v\right)=\frac{m_0}{{\left[1-{\left(v/c\right)}^2\right]}^{3/2}}$ (3)

于是图1中的(F)环节为

$\text{d}y=\text{d}\left(\frac{m_{0}v}{\sqrt{1-{\left(v/c\right)}^2}}\right)=y^{\prime }\left(v\right)\text{d}v=\frac{m_0}{{\left[1-{\left(v/c\right)}^2\right]}^{3/2}}\text{d}v$ (4)

由此得到图1中的(H)环节

${\displaystyle \underset{0}{\overset{v}{\int }}v\text{d}\left(\frac{m_{0}v}{\sqrt{1-{\left(v/c\right)}^2}}\right)}=m_0{\displaystyle \underset{0}{\overset{v}{\int }}\frac{v\text{d}v}{{\left[1-{\left(v/c\right)}^2\right]}^{3/2}}}$ (5)

注意到这是一个以被积函数的自变量v为上限的变限积分。输入下列命令，

>> syms v c m0

>> m0*int(v/(1-(v/c)^2)^(3/2),v,0,v)

显示的信息为

??? Error using ==> sym/maple

Error, (in limit) invalid limiting point

表明MATLAB无法直接计算式(5)所示的自变量v为上限的变限积分。需要指出的一点是，由于MATLAB不是一个开源软件，在满足MATLAB使用规则的前提下，对于MATLAB不能计算的情况，无法追溯到MATLAB源码处理层次找到运算过程，看一看它为什么不能计算，具体到这里的情况，无法解释到底为什么出错或者为什么不能计算，也无法补充支持不规范的源码级运算过程内容，只能选择接受或者不接受。

下面换一个角度来看一看图1中的(H)环节即式(5)的计算问题。文献 [3] 第294~295页给出了一道例题33，为了方便对比，现将该例题及有关证明部分摘录如下：

设函数f(x)在闭区间 $\left[a,b\right]$ 上具有连续的二阶导数，试证：存在 $$，使得

${\displaystyle \underset{a}{\overset{b}{\int }}f\left(x\right)\text{d}x}=\left(b-a\right)f\left(\frac{a+b}{2}\right)+\frac{1}{24}{\left(b-a\right)}^3{f}^{″}\left(\xi \right)$ (6)

证法一：设 $F\left(x\right)={\displaystyle \underset{a}{\overset{x}{\int }}f\left(x\right)\text{d}x}$，在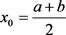的二阶泰勒公式为

$\begin{array}{l}F\left(x\right)={\displaystyle \underset{a}{\overset{x}{\int }}f\left(x\right)\text{d}x}={\displaystyle \underset{a}{\overset{\frac{a+b}{2}}{\int }}f\left(x\right)\text{d}x}+f\left(\frac{a+b}{2}\right)\left(x-\frac{a+b}{2}\right)\\ +\frac{1}{2!}{f}^{\prime }\left(\frac{a+b}{2}\right){\left(x-\frac{a+b}{2}\right)}^2+\frac{1}{3!}{f}^{″}\left({\xi }_1\right){\left(x-\frac{a+b}{2}\right)}^3\end{array}$ (7)

式(7)中的 ${\xi }_1$ 在 $\left(a+b\right)/2$ 和x之间。该题后面的证明过程与本文无关，暂略。

具体到式(5)来说，其中的被积函数可以记为

$f\left(v\right)=\frac{v}{{\left[1-{\left(v/c\right)}^2\right]}^{3/2}}$ (8)

利用diff( )可以求出其一阶导数

>> diff(v/(1-(v/c)^2)^(3/2),v)

ans =1/(1-v^2/c^2)^(3/2)+3*v^2/(1-v^2/c^2)^(5/2)/c^2

即

$f^{\prime }\left(v\right)=\frac{1}{{\left[1-{\left(v/c\right)}^2\right]}^{3/2}}+\frac{3}{{\left[1-{\left(v/c\right)}^2\right]}^{5/2}}\cdot {\left(\frac{v}{c}\right)}^2$ (9)

利用diff( )还可以求出其二阶导数

>> diff(v/(1-(v/c)^2)^(3/2),v,2)

ans = 9/(1-v^2/c^2)^(5/2)*v/c^2+15*v^3/(1-v^2/c^2)^(7/2)/c^4

即

$f^{″}\left(v\right)=\frac{9v}{c^2{\left[1-{\left(v/c\right)}^2\right]}^{5/2}}+\frac{15v^3}{c^4{\left[1-{\left(v/c\right)}^2\right]}^{7/2}}$ (10)

比较一下式(5)和(7)，如果再把一阶导数表达式(9)和二阶导数表达式(10)代入，可以看出在图1所示的计算过程中难以从(H)得到(I)。那么(I)是如何得到的？

在MATLAB中输入下列语句

>> syms v c m0

>> simple(m0*int(v/(1-(v/c)^2)^(3/2),v,0,w))

化简后的最终结果为

ans =m0*c^2/(1-1/c^2*w^2)^(1/2)-m0*c^2

即

$E=\cdots =m_0{\displaystyle \underset{0}{\overset{w}{\int }}\frac{v\text{d}v}{{\left[1-{\left(v/c\right)}^2\right]}^{3/2}}}=m_0{c}^2\left(\frac{1}{{\left[1-{\left(w/c\right)}^2\right]}^{1/2}}-1\right)$ (11)

得到这个形式的结果仅仅是因为改变了一下积分上限的符号；换言之，在图1所示的计算过程中，从(F)环节到(H)环节，积分上限均为被积函数的自变量v；等到(H)环节要具体计算定积分的时候，先把v换成另外一个非自变量符号例如w，得到积分结果以后再将w换回v，于是得到了(I)环节所示的结果，即

(12)

但是这种处理方式无论是从逻辑还是从数学角度来看都是不正确的，在这种情况下，再讨论后面的处理步骤已经没有任何意义。换言之，在规范使用数学工具和满足逻辑一致性的前提下，按照图1所示的步骤不可能推导出E = Mc²。

3. 从物理和数学角度推导E = Mc²的方法

质量、能量和速度三者之间在量纲上存在下列关系

$能量\equiv 质量\times {\left(速度\right)}^2$ (13)

式中的“≡”表示量纲意义上的等价关系。以式(13)为基础，可以分别从物理和数学角度简捷地导出E = Mc²，文献 [4] [5] 详细了有关推导过程，感兴趣的读者可以参阅，本文不再重述。

4. 结束语

本文基于MATLAB的详细分析验算结果表明，在规范使用数学工具和满足逻辑一致性的前提下，按照图1所示的步骤不可能推导出E = Mc²。如果图1所示的推导过程就是相对论体系中导出E = Mc²的方法，并且除此之外没有其他方法，那么将引发对相对论基础的质疑。

另一方面，E = Mc²是有物理意义的，当然这种物理意义与相对论所说的物理意义是不相同的。基于量纲分析方法，可以分别从物理角度和数学角度简单地导出E = Mc²。