1. 引言
对于一个图
,我们设
,
和
分别表示
的顶点集,边集和弧集,
表示
的全自同构群;
称为图
的阶。如果群
作用在
,
或
上传递,则分别称
为G-点传递图,G-边传递图或G-弧传递图。特别地,弧传递图也称为对称图。对任意的
,定义
为点u的邻域,称
为点u的度数,记为
。如果对任意的
,u和v的度数相等,则称 为正则图,
为图
的度数,记作
。给定一个正整数s和
上的
个点
,称
是一条s-弧,如果
,且
和
是邻接的。若
在
的s-弧集上传递,则称
为
-弧传递图;如果
是
-弧传递图但不是
-弧传递图,则称
为
-传递图。特别地,一个
-传递图可简单的称为s-传递图。
在代数图论中,阶数特定的对称图受到了国内外学者的广泛关注。例如:文献( [1] )给出了不大于768个点的三度图的分类。设
为素数,在文献( [2] [3] [4] )中,作者分别分类了p,2p,3p阶的对称图;之后,Praeger等在( [5] )和( [6] )中分别将其推广到pq阶的对称图。1947年,Tutte在文献( [7] )中确定了3度图的点稳定子群的结构,在此之后的几十年里,3度对称图引起了大量学者的研究,他们给出了3度对称图的各种构造方法及其分类。例如,Du和Wang在文献( [8] )中考虑了单群
上的3度Cayley图,其中r为一个素数的方幂;Feng等在( [9] )中分类了阶为8p和8p2的3度对称图;Zhou和Feng在( [10] )中对2pq阶的3度对称图进行了分类。
设
是一个传递置换群,则称X是拟本原的,如果X的每个极小正规子群都在
上传递;称X是二部拟本原的,如果X的每个极小正规子群在
上至多有两个轨道并且存在一个极小正规子群作用在
上恰有两个轨道。给定一个图
,
,称
是一个G-基图,如果G在顶点集
上是拟本原的或者二部拟本原的。研究对称图的一般分为以下两步:
第一步,研究对称图的基图;
第二步,刻画对称图的基图的正规覆盖。
基图的分类是研究对称图的基础,它不仅可以为学习对称图提供一些图例,而且对于后续研究基图的覆盖有着重要的参考作用。设
是一个阶为
的3度对称图,本文将分类
的G-基图,其中
为素数,
,
,所得主要结论如下:
定理1.1:设
为素数,
是一个阶为
的3度G-基对称图,其中
,
,则
满足表1。
2. 预备知识
本文所考虑的所有图均为有限的、非空的、无向的、连通的、以及没有圈和重边的正则图。关于本文所使用的群论和图论的符号和基本概念都是标准的,可以参看学者们的著作( [11] [12] [13] [14] )等。例如:

Table 1. 3 degree G-based symmetry diagram of order 2 p m q n
表1. 阶为
的3度G-基对称图
我们用
表示n阶循环群,
和
分别表示交错群和对称群。
本节的主要内容是给出一些重要的结论和例子。首先我们给出由Tutte于1947年确定的3度对称图的点稳定子群的结构,它为我们研究3度对称图奠定了基础。
引理2.1 ( [7] ):设
是一个连通的3度
-弧传递图。则
,并且
满足表2,其中α∈VΓ。

Table 2. Point-stabilized subgroups of 3-degree symmetry maps
表2. 3度对称图的点稳定子群
设G是一个有限群,H是G的子群。令D为H在G中的若干个形如
的双陪集之并。定义群G上关于H和D的陪集(有向)图
如下:顶点集
,即H在G中的所有右陪集之并,边集
。陪集图有如下的性质。
引理2.2 ( [14] ):设
是群G关于H和D的陪集有向图,则
1)
是点传递图,并且
;
2)
是连通图当且仅当
;
3)
是无向图当且仅当
;
4)
是G-弧传递的当且仅当
是一个单个的双陪集。
陪集图通常用于构造一些图例,下面的4个例子是根据3度图的点稳定子群的结构以及陪集图的性质构造而成,可参看文献( [1] )和( [10] )。
例2.3:1) 设
,则G有一个子群
,且存在一个对合x使得
,
。于是由引理2.2知陪集图
是一个阶为182的3度对称图,记为
,且
。
2) 设
,则G有一个子群
,且存在一个对合x使得
,
。于是由引理2.2知陪集图
是一个阶为182的3度对称图,记为
,且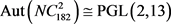 。
。
例2.4:1) 设
,则G有一个子群
,且存在和一个对合x使得
,
。于是由引理2.2知陪集图
是一个阶为506的3度对称图,记为
,且
。
2) 设
,则G有一个子群
,且存在和一个对合x使得
且
。于是由引理2.2知陪集图
是一个阶为506的3度对称图,记为
,且
。
例2.5:设
,则G有一个子群
和一个对合x使得
且
。于是由引理2.2知陪集图
是一个阶为2162的3度对称图,记为
,且其全自同构群为
。
例2.6:1) Levi图
是唯一的一个阶为30的3度对称图,它是5-正则的二部图且
。
2) Smith-Biggs图
是唯一的一个阶为102的3度对称图,且
。
3) Coxter-Frucht图
是唯一的一个阶为110的3度对称图,且
。
对于给定的较小群G,利用Magma ( [15] )软件计算包可以确定所有同构意义下的G-弧传递图。通过Magma ( [15] )直接计算,我们可得以下的5个例子。值得注意的是,在例子中所出现图,它们在同构意义下都是唯一的。
例2.7:1) 设
,则G有一个子群
,由Magma ( [15] )可知,存在一个阶为20的3度对称图,记为
,且
。
2) 设
,则G有一个子群 ,于是通过Magma ( [15] )计算,存在一个阶为20的3度对称图,记为
,且
。
,于是通过Magma ( [15] )计算,存在一个阶为20的3度对称图,记为
,且
。
例2.8:设
,则G有一个子群
或
,于是存在两个3度对称图,分别记为
和
,它们的阶分别为28和56,且
,
。
例2.9:设
,则G有一个子群
或
。通过Magma ( [15] )计算可得:
1) 如果
,则存在一个阶为28的3度对称图,记为
,且
。
2) 如果
,则存在两个阶为56的3度对称图,分别记为
和
,且
,
。
例2.10:1) 设
,则G有一个子群
,通过Magma ( [15] )计算,存在一个阶为650的3度对称图,记为
,且
。
2) 设
,则G有一个子群
,由Magma ( [15] )可知,存在一个阶为650的3度对称图,记为
,且
。
例2.11:1) 设
,则G有一个子群
,存在一个阶为234的3度对称图,记为
,且
。
2) 设
,则G有一个子群
,故由Magma ( [15] )计算,存在一个阶为234的3度对称图,记为
,且
。
下面的引理是( [16],引理2.5])的一个特例,它略微改进了Praeger的结论( [17],定理4.1])。
引理2.12 ( [16] ):设
是一个连通的奇素数度的G-弧传递图,
有一个非传递的正规子群N在 上至少有两个轨道。则下面的陈述成立:
上至少有两个轨道。则下面的陈述成立:
1) N在
上半正则,
,
是G/N-弧传递的,并且
是
的正规N-覆盖。
2)
是
-弧传递的当且仅当
是
-弧传递的,其中
或
。
3)
,其中
,
。
3. 定理1.1的证明
为了完整的证明定理1.1,我们先证明以下两个引理,第一个引理分类了一类单群。
引理3.1:设T是一个非交换单群且满足
,且
,其中
为素数,
。则下列之一成立,其中
表示
的所有素因子的个数。
1) 如果
,则
满足表3。

Table 3. Single group T with 3 prime factors
表3. 含有3个素因子的单群T
2) 如果
,则
满足表4。

Table 4. Single group T with 4 prime factors
表4. 含有4个素因子的单群T
证明:因为
,所以
,因此T满足( [18],定理I)。
如果
,则
或3,
,因此T是一个
-群。如果
,则
,于是
,故由( [18],表1)可知:
或
,此时,
或
。如果
,则
,故
。再由( [18],表1)可得:
,
,
,
,
,
或
。
如果
,由
可知
,因此T是一个
-群,于是由( [18],定理I)可知:T满足( [18],表2)或者T同构于单群
,其中
为一个素数的方幂。如果T满足( [18],表2),则通过检查它们的阶可得:
,此时
。如果
,则由( [18],定理3.2和引理3.4(2),3.5(2))可知:要么
,要么
是一个素数。
假设
,其中
是一个素数,则
。注意到, ,因此,
,因此,
即
因为
,所以
或
,即
或
。由此可得:
,13,17,23,31,47或97。通过检查它们对应单群
的阶可知:满足条件的q为11,13,23,31,47,97。□
假设
为素数,
是一个连通的阶为
的3度G-弧传递图,其中
,
。设N是 的一个极小正规子群,则
,其中T是一个单群且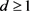 。令
。
。令
。
引理3.2:应用上面的符号说明。如果N是非交换的,则
。
证明:反证法。假设
,则由
可知:
。如果N在
上至少有3个轨道,则由引理2.12可知,N在
上半正则,于是
,注意到
,矛盾。故N在
上至多有2个轨道。令
,其中
。
假设N在
上传递。由
且
是连通图可得:
。因此,
是传递的且
是N-弧传递的。如果
在
上传递,则由( [12],定理4.2A)可知:中心化子
在
上半正则,从而
在
上半正则,这与
不能整除
相矛盾。如果
在
上至少有3个轨道,则由引理2.12可知:
在
上半正则,矛盾。因此,
在
上恰好有2个轨道,记为U和W。因为
,故U和W构成
上的一个N-不变块系,于是
在N中的指数为2。但是,
没有指数为2的子群,矛盾。
假设N在
上恰有两个轨道,记为
。此时,
是一个二部图,其二部分别为
和
。令
。如果
作用在
上是非忠实的,则由( [19],引理5.2)可知: 是一个完全二部图,于是
,因此,
,矛盾。如果
作用在
上是忠实的,则
可以看作
上的一个传递置换群。如果
在
上传递,则由( [12],定理4.2A)可知:
在
上半正则,故
,矛盾。因此,
在
上至少有2个轨道,故由( [20],引理3.2)可知:
在
上半正则,矛盾。□
是一个完全二部图,于是
,因此,
,矛盾。如果
作用在
上是忠实的,则
可以看作
上的一个传递置换群。如果
在
上传递,则由( [12],定理4.2A)可知:
在
上半正则,故
,矛盾。因此,
在
上至少有2个轨道,故由( [20],引理3.2)可知:
在
上半正则,矛盾。□
下面给出定理1.1的完整证明。
定理1.1的证明:设
是一个连通的阶为
的3度对称G-基图,则G在
上是拟本原的或者二部拟本原的,其中
为素数,
,
。设N是G的一个极小正规子群,则
,其中T是一个单群且
。令
,下面我们分两种情形来完成定理1.1的证明。
情形1:假设G在
上是拟本原的。
此时N在
上是传递的。如果N是一个交换群,则N在
上正则,从而
,矛盾。因此N是非交换的,于是由引理3.2可知:
,从而
。进一步,由于
,则
是T-弧传递的,因此
满足引理2.1,于是
。由T的传递性可得:
整除
。另一方面,由于
是T-弧传递的,则
,于是
。故T满足引理3.1。
假设
,则T和
满足下表5。

Table 5. Single group T with three prime factors and its corresponding ( p m , q n )
表5. 含有3个素因子的单群T及其对应的
如果
,则
,从而
,故由例2.7可知
。如果
,
或
,则
,从而由( [10] )可知:只有当
时才存在满足条件的图
,此时T有一个子群
。由例2.6可知
。如果
,且
或
,则
或3,从而由引理2.1可得,
或
。由例2.8可知
或
。如果
,则
,但是,
没有子群同构于
,这与引理2.1相矛盾。如果
,则
且
。由例2.11可知:
。
假设
,则T和
满足下表6。

Table 6. Single group T with four prime factors and their corresponding ( p m , q n )
表6. 含有4个素因子的单群T及其对应的
如果
,其中 ,则
,由( [10] )可知,只有当
,23或47时才存在满足条件的图
,进一步,由例2.3,2.4和2.5可得,
,
或
。如果
或
,则
。但是,
和
都没有子群同构于
,这与引理2.1相矛盾。如果
或
,则
或
,此时
或
,由Magma ( [15] )计算可知,此时不存在满足条件的图
。
,则
,由( [10] )可知,只有当
,23或47时才存在满足条件的图
,进一步,由例2.3,2.4和2.5可得,
,
或
。如果
或
,则
。但是,
和
都没有子群同构于
,这与引理2.1相矛盾。如果
或
,则
或
,此时
或
,由Magma ( [15] )计算可知,此时不存在满足条件的图
。
情形2:假设G在
上是二部拟本原的。
此时,G有一个极小正规子群
在
上恰有两个轨道,分别记为
和
。于是,
是一个二部图,并且其二部分别为
和
。令
,则
,
,
。如果N是交换的,则N在
上正则,从而
,矛盾。因此N是非交换的。由引理3.2可知:
是一个非交换单群。如果
作用在
或
上是非忠实的,则由( [19],引理5.2)可知:
是一个完全二部图,于是
。故,
,矛盾。假设
作用在
和
上是忠实的,则由( [21],定理1.5)可知下列之一成立:
(a)
在
上是拟本原的;
(b)
有两个正规子群
,
满足
且它们在
半正则。进一步,群
在
上正则。
对于情形(b),有:
,矛盾。下面考虑情形(a)。假设
在
上是拟本原的,则
有一个极小正规子群T且T是一个单群,于是由O’Nan-Scott-Praeger定理( [17] )可知:
或
。如果
,则
是全形单型,且T在
上正则。因此 ,矛盾。故
。进一步,如果T不是G的唯一极小正规子群,则由
可知
,于是G的正规子群
,矛盾。故
。进一步,如果T不是G的唯一极小正规子群,则由
可知
,于是G的正规子群 在
上有
个轨道,这与G在
上是二部拟本原的相矛盾。故,T是G的唯一极小正规子群,即G是几乎单的且其基柱
。令
,
在
上有
个轨道,这与G在
上是二部拟本原的相矛盾。故,T是G的唯一极小正规子群,即G是几乎单的且其基柱
。令
, ,其中
且
。由于
,于是由引理2.1可知
,其中
且
。由于
,于是由引理2.1可知 ,因此
整除
。另一方面,由于
,则
,
。故T满足引理3.1。
,因此
整除
。另一方面,由于
,则
,
。故T满足引理3.1。
假设
。此时T和
满足表5。如果
,则由Altas ( [22] )可知
。因此
,
,且 ,于是由引理2.1可知,
。故由例2.7可知
。如果
,则
,于是
或
。若
,则
,于是
,由Magma ( [15] )计算可知:此时不存在满足条件的图
。若
,则
,于是
,由例2.6可知
。如果
,则
,且
或
。于是
,并且G有两个子群分别同构于
和
。故由例2.9可知:
,
,或
。如果
,则由Altas ( [6] )可知
,此时与
且
相矛盾。如果
,则
,于是
,此时
,这与引理2.1相矛盾。如果
,则
,从而
,此时
,由例2.11可知
。如果
,则
,故
,此时
,但是,
不存在48阶的子群,矛盾。
,于是由引理2.1可知,
。故由例2.7可知
。如果
,则
,于是
或
。若
,则
,于是
,由Magma ( [15] )计算可知:此时不存在满足条件的图
。若
,则
,于是
,由例2.6可知
。如果
,则
,且
或
。于是
,并且G有两个子群分别同构于
和
。故由例2.9可知:
,
,或
。如果
,则由Altas ( [6] )可知
,此时与
且
相矛盾。如果
,则
,于是
,此时
,这与引理2.1相矛盾。如果
,则
,从而
,此时
,由例2.11可知
。如果
,则
,故
,此时
,但是,
不存在48阶的子群,矛盾。
假设
。此时T和
满足表6。如果
,
或
,则
,于是
,
或
。此时,
,这与引理2.1相矛盾。如果
,则
,此时与
且
相矛盾。如果
或
,则
,于是
或
。若
,则
,但是,G没有子群同构于
,这与引理2.1相矛盾。若
,则
,这与引理2.1相矛盾。如果
,则
,于是
,
,然而,G没有子群同构于
,矛盾。如果
,
或
,则
,故
,
或
,进一步可得,
或
。故由例2.3,2.4和2.6可知:
,
或
。如果
,则
,于是
或
。因此,
或
。由例2.10可知
或
。□
基金项目
国家自然科学基金资助项目(80031010061)资助。