1. 引言
近年来,复杂网络的研究受到学者的关注。复杂网络的理论与模型也得到了极大的丰富。大家结合自己的研究领域,研究对象的特征,对相关模型进行改进。Chen [1] 为了研究Internet网中拓扑特性产生的机理,建立了多局域世界演化模型,在该模型中,整个网络由多个独立的局域网组成,网络的演化就如新节点的加入,边的增加,边的删减都在局域网中进行,仅对该局域网中节点的度产生影响,对其他局域网节点没有太大影响;后来学者们又根据研究所需对该模型进行改进,田思 [2] 根据现实网络的局域性及联系的强弱,将权重引入到多局域世界模型之中,构造了加权多局域世界演化模型;李晓 [3] 将局域性与赋权性加入到全局无权网络,构造了多局域加权n网络,并进行仿真模拟,研究模型的拓扑性质。
现实生活中的大多数网络虽然包含多个局域网,但局域网却不像多局域世界网络模型 [4] 中的局域网那样均匀,它们有着不同数量的节点,不同数量的边,甚至局域网之间还存在着竞争关系。如国际对外直接投资网络,可以根据国家所处地区将整个投资网络分成不同的区域(局域网),且每个区域中的国家数量不同,各个区域中国家间投资关系联系的紧密程度不同,即每个区域规模不同;由于各个区域发展程度不同,对外政策,开放程度不同,所以每个区域增加新投资关系的可能性也不同,即区域之间存在竞争关系,所以在运用多局域世界网络模型取刻画投资网络时,会发现存在很多局限。本文尝试在多局域世界网络模型的基础之上,引入局域网间的不等性,竞争性,构造改进的多局域世界网络演化模型,并对该模型的度分布进行研究。
2. 模型建立与分析
2.1. 改进的多局域世界模型(IMLW)
多局域世界网络的初始条件是有着m个拥有
个节点和
条边的局域网络,且这m个局域网之间节点数,边数都相同,局域网间也不存在竞争关系。但对于现实生活中的许多网络而言,它虽然也包括多个起始的网络,但它们之间并不是均等的,这些网络有着不同的节点数和边数,对新节点有着不同的吸引力,也就是说,局域网络之间存在着竞争。那么,为了使得模型更贴合现实生活中的网络,需要对多局域世界网络进行改进,使得改进的网络模型更加确切的解释真实网络的结构特征的产生机理。
初始条件:起始为m个独立的局域网,每个网络有
个节点和
条边(
),(记
,即初始网络中总共有M个节点),且局域网之间存在着竞争,赋予每个局域网
一个参数,表明该局域网竞争系数
,接下来每一个时间步长内,都进行如下的操作:
1) 以概率
增加一个新节点到一个选定的局域网中,且与该局域网中的节点建立
条边。首先需要选定一个局域网Ωp,其概率为
(2.11),接下来新节点与该网络节点i连接的概率为按照度择优的原则
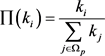 。 (2.12)
。 (2.12)
2) 以概率
增加
条边到选定的局域网中。首先需要选首先按照2.11式选定一个局域网
,随机
选择该网络中的一个节点,概率为
,接下来按2.12式选定另一个节点,重复上述过程 次。
次。
3) 以概率
在选定的局域网中去掉
条边。首先需要选定一个局域网
,根据反择优原则,那么一个局域网的竞争力越低被选择的概率就越大。选定局域网Ωp的概率为
,接下来随机选择一个节点,概率为
,然后反择优选择另一节点,其概率为
4) 以概率
选定一个局域网,让其与其它局域网建立
条长程边。首先按照2.11选定一个局域网Ωr,然后在该网络中按照2.12式选定一个节点,再按2.11式选择一个局域网Ωp,并在该局域网中按2.12式选择一个节点与之前节点相连,重复上述过程
次。
5) 终止条件,运行N步。
其中
,改进的多局域世界网络模型最终生成的网络为m个大小不均的局域网,每个局域网中的节点数,边数都不等。局域网间紧密程度,节点数,边数差距的取决于初始网络中各局域网的竞争力
,竞争系数越大的局域网,在整个演变过程中增加节点,边的几率越大,最终的局域网规模越大,节点间的联系越密切。若
中存在某一个局域网的竞争系数远远大于其它局域网的竞争系数,那么最终的网络由一个规模较大的局域网和几个规模较小的局域网构成。
2.2. 度分布分析
接下来采用解析方法中的平均场理论来求解改进多局域世界网络模型的度分布,具体计算过程如下:
1) 增加一个带有
条边的节点到一个选定的局域网Ωp中。
(2.13)
2) 增加
条边到选定的局域网中。
(2.14)
3) 在选定的局域网中去掉
条边。
(2.15)
4) 选定一个局域网,让其与其它局域网建立
条长程边。
(2.16)
经过t个时间步长后,整个网络中增加的节点数为
,局域网中增加的节点数与局域网的竞争系数成正比,局域网的竞争系数越大,增加的节点数就越多。局域网Ωp增加的节点数为
,每个局域网中的节点数应当是初始时刻局域网所含的节点数加上增加的节点数,局域网Ωp中的节点数目为
(2.17)
当时间t无限大时,可以忽略
的影响,则
(2.18)
经过t个时刻后,节点的总度增加了
,令
,则
,局域网增加度与局域网的竞争系数成正比,局域网
增加度
,局域网Ωp中的度等于初始时刻局域网中的度与t个时刻增加的度之和,故
,当时间t无限大时,
(2.19)
则度对时间的变化率为
(2.20)
令
,
将a和b代入(2.20)式,并化简可以得到
由初始条件为
可得
由于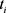 服从
的均匀分布,则
服从
的均匀分布,则
则度的密度分布函数
由此可知该网络模型的度服从幂律分布,为无标度网络,其中
,
的取值影响着幂指数的值,当
取值均相同时,幂指数的值介于1~2之间。
3. 仿真模拟
我们运用MATLAB进行仿真模拟,绘制出有着
个独立局域网,
,
,
,
,
,
,
,
,
,多局域世界网络模型中每个局域网中节点数边数相同为
改进多局域世界网络模型中各局域网的节点数、边数、竞争系数定义为
,
,
,
,
,
,
,
,
,
,绘制出两个模型的网络的度在对数坐标系中的分布情况,如图1,图2所示,比较图1,图2可以看出多局域世界网络模型的度分布比较均匀,网络中节点度的最大度仅为10,最大度与最小度的差距较小,而在改进的多局域世界网络模型中,度分布比较分散,最大度接近100。相比较而言,改进的多局域世界网络模型更加贴合现实生活中的网络。

Figure 2. IMLW degree distribution
图2. 改进多局域世界网络度分布
4. 小结
本文在多局域世界演化模型的基础之上,将局域网之间的不等性、竞争性引入到模型之中,建立了改进的多局域世界网络模型,并运用平均场理论对改进多局域世界网络模型的度分布进行求解,改进模型度服从幂律分布,幂指数的大小与每个局域网的竞争系数有很大关系。最后进行仿真模拟,改进模型网络度的分布与原模型度分布相比度的分布更不均匀,更加贴合现实生活中的网络,实用性更强。