1. 引言
在正n边形的n条边上顺序截取等长线段得到n个截点,它们一定能顺序成为某个正n边形的n个顶点。这就是大家熟知的正多边形等截分问题,其证明是简单的,但其逆问题的求解 [1] [2] [3] [4] 却不是那么显然的。文献 [1] [2] [3] [4] 分别讨论了n = 3和n = 4的情况。本文将统一考虑正n边形的等截分问题的逆问题并给出解析研讨。
延续文献 [4] 的想法,不仅可以考虑等长截点落在原n边形各边之上,还可以考虑截点落在各边的有向延长线上。显然推广了的正n边形等截分点相应性质依然具备,同时逆问题也有相应的推广。本文将沿用文献 [4] 的方法并进一步拓展,自然推广原有结果。
本文不仅得到了正n边形的等截分逆问题的一些看起来有点神奇结果,同时也得到了文献 [1] [2] [3] [4] 中没有提到的一些关于三角形等截分逆问题的新的结果。比如除了正多边形外,凸偶数边形可以各边的内部有等截分正多边形(定理1),而凸奇数边形只有五边形才可以(定理5);而如果考虑等截分点都在各边延长线上,则不管奇偶性,凸多边形等截分能得到正多边形的只有原来就是正多边形的情况(定理3)。最后的定理6和定理8则说明对三角形的情况,非平凡的等截分解存在且仅存在于钝角三角形之中。
2. 准备工作
文献 [4] 是从正方形的内角和作为一个出发点来考虑问题的,我们延续这种想法,但是换用更本质的外角和来考虑问题。
以下总考虑顺序以点
为顶点的正定向n边形
,
。记顶点Ai到Ai+1的边长为
,顶点Ai之处的有向外角为
,以有向截长
在边AiAi+1或其延长线上从Ai出发所截得之点为
,其中记
,
,
,
,
,
;
,
,
。熟知有
(1)
先给出一个正n边形等截分问题的一个等价条件。
引理1:上述正定向n边形
的以有向截长
确定的等截分点n边形
恰好成为正n边形的充要条件是其边长、外角以及等截长满足(1)式以及
(2)
(3)
其中
。并且,在指标n阶循环意义下的任意指定的2个相邻i所对应的(2)和(3)式中2对方程,蕴含于整个方程组的其余2n - 3个方程之中。
证明:等截分点n边形
是正n边形的充要条件是其n个边向量
循序旋转2p/n相等。
正n边形的各组相邻边的关系相同,故只需要首先分别考虑Pi-1Pi和PiPi + 1成为某个正n边形的一组相邻边的充要条件。
为此,以Ai为原点、以AiAi+1为横轴正向向量建立直角坐标系,如图1所示,则各点坐标可分别确定为
,
,
,
,
,
。此时,n边形
的边向量
,
。
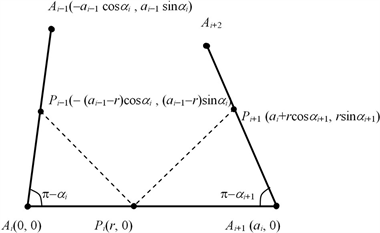
Figure 1. Sketch map of equal segmentation
图1. 等截分示意图
同时,这两条边向量旋转
相等的条件在此坐标系下的表达形式即为
(4)
分量形式即分别为
它们分别对应于(2)和(3)式中指标i相同的一对方程。
注意到(2)和(3)式之中的几何量与坐标系选取无关,故与(1)式联立时等价于等截分点n边形
的n个边向量
循序旋转
是相等的,从而是它成为正n边形的充要条件。进一步,注意到在指标循环意义下的n - 2对相邻边向量循序旋转
相等,则蕴涵着另外两对也同时成立,其中外角取值满足(1)式,因而结论成立。
引理2:上述正定向n边形
若具有以有向截长
所分别确定的等截分点n边形分别为正n边形,则
必为正n边形,从而其对于任意截长所得到的等截分点n边形均为正n边形。
证明:对于给定的正定向n边形
,若以有向截长
所分别确定的等截分点n边形分别为正n边形,则由引理1结论,(2)和(3)式对于
和
都成立,注意到各边长
,得到
其中
。注意到
,该组条件意味着只能有
代回(2)式进一步得到
,即得
为正n边形。
引理3:上述正定向n边形
若仅具有唯一的有向截长
使得所确定的等截分点n边形
恰好为正n边形,则在(1)式联立(2)式、(3)式所得到的方程组之中,(3)式等价于方程
(5)
而(2)式当
时可以等价置换为方程
(6)
其中
。
证明:现在
不是正n边形,否则由引理2可知矛盾。由引理1证明过程可知,(2)式对应等价于
(7)
其中
。同时(3)式等价于(5)式,并且可以按指标组等价改写为
(8)
现在,(7)、(3)、(8)式所对应3元线性方程组有非零解
的充要条件是其系数矩阵的行列式为零,即有
此即按指标组等价于(6)式。注意到当
时(6)式意味着(7)式可由方程(3)和(8)式线性表出,故此时(2)式可以等价置换为方程(6)式,结论得证。
引理4:上述正定向n边形
若是凸的并且仅具有唯一的有向截长
使得所确定的等截分点n边形
恰好为正n边形,则当n = 3或n = 4时,或当n ³ 5并且
时,(1)式联立(2)式、(3)式所得到的方程组等价于(1)式联立(5)、(6)式所得到的方程组。
证明:现在
具有正定向且凸,意味着
。由引理2可知它不是正n边形,由引理3可知现只需证明
。
用反证法,不妨设
使
,则
,此时(2)、(3)式对应于指标i分别取为j和j + 1而化简得到两组等式
进而,由第二组式子可知,当n = 3时,若
则进一步由(1)式即可得知
,矛盾;于是此时只能有
当n = 4时,同样由第二组式子易知
而当n ³ 5并且
时,由第一组式子可知
于是在每种情形下都可递推得到
各外角相同、各边等长,与它不是正n边形矛盾。结论得证。
引理5:对于给定的不是正n边形的正定向n边形
,若存在一致小于(或一致大于)各边之长的有向截长
使其所确定的等截分点n边形
恰好为正n边形,则
的外角不能有取值
的。
证明:若 使某个外角
,则(2)式和(3)式蕴涵
使某个外角
,则(2)式和(3)式蕴涵
现
或
,则
注意到
,即得唯一解
。关于指标j递推归纳则得n个外角都等于
,再回到(2)式得到各边长也都相等,与
不是正n边形矛盾。得证。
3. 主要结果
有了前述的准备工作,本节给出本文的几个主要结果。为了便于叙述,先分奇偶性讨论一下。
对于一般的偶数边凸n边形,考察当
,
时的情形下的特解及其性质。注意到此时
,由(6)式可知
故有
。于是方程组(6)式和(1)式有特解
,此时(5)式有对应解
从而满足对
都有
即由引理4和引理1可知对于边数为偶数n ³ 6的情形都对应有不是正多边形的一族解,且此情形有
于是,对于偶数n ³ 6的情形,可如此构造出正n边形等截分点逆问题的一族凸n边形非平凡内截之例。即得下列结论。
定理1:对于偶数n ³ 6的情形,至少存在不是正n边形的一族凸n边形,具有唯一的小于各边之长的有向截长,使得其各边之上的等截分点顺序构成正n边形。
对于奇数边数n ³ 7的情形,类似的结论并不成立。事实上有下列结论。
定理2:对于奇数边数n ³ 5的情形,上述正定向n边形
若是凸的并且仅具有唯一的一致小于各边之长的有向截长
使得所确定的等截分点n边形
恰好为正n边形,则奇数边数只能是n = 5。
证明:现在
具有正定向且凸并且仅具有唯一的小于各边之长的有向截长,意味着
。而由引理2可知它不是正n边形,由引理4、引理5可知相关各量是(1)、(5)、(6)式联立所得方程组的解,且
。
此时(5)式对应等价变形为
(9)
从而由条件
推出
(10)
由(1)式以及
可知
使
,则由(10)式可知
,故得
。再由(10)式递推可知
,故得当奇数边数n = 5时
,而当奇数边数n ³ 7时必有
。当奇数边数n ³ 7时,随着指标i顺序遍历
,外角
在两个不相交的区间
和
交替取值,将得到矛盾;故只有当n = 5时的情形需进一步考虑外角取值分布的相容性。结论得证。
定理3:对于凸的上述正定向n边形
,若具有一致大于各边之长的有向截长r使得所确定的等截分点n边形
恰好为正n边形,则
只能是正n边形。
证明:用反证法。设凸正定向
不是正n边形,且具有有向截长
使得所确定的等截分点n边形
恰好为正n边形,则凸正定向意味着
。由引理2、引理4可知相关各量是(1)、(5)、(6)式联立所得方程组的解,也等价是(1)、(2)、(3)式联立所得方程组的解。
此时(5)式对应等价变形为
(11)
特别当n = 3时即为三个内角
的形式
(12)
当n ³ 4时,由(1)式和凸性不妨设
,则(11)式蕴涵
进而按两个区间分两种情形分别讨论。若
,则由(11)式递推有
于是
进而再由(1)式归纳可得
再回到(2)式可得
此时与
不是正n边形的假设矛盾,故该种情形不成立,从而只需考虑另一情形
。此时,同理(11)式蕴涵
,且只需再考虑情形
即可。递推归纳后,依然得到各外角相等、各边长相等,此时亦与
不是正n边形的假设矛盾,即知
只能是正n边形。
当n = 3时,由(1)式不妨设
,则(12)式蕴涵
再由(1)式限制可知只能有
再由(12)式可知
于是
进而得到各内角相等、各边长相等,此时亦与ΔA
1 A
2 A
3不是正三角形的假设矛盾,故该假设不成立,即结论得证。
与上述证法类似,利用(12)式也可推知关于三角形的下列结论成立。
定理4:若在ΔA
1 A
2 A
3三边A
1 A
2、A
2 A
3、A
3 A
1之上(不含延长线上)可以分别截取点P1、P2、P3使得有向截长A1P
1 = A
2P
2 = A
3P3并使ΔP1P2P3成为正三角形,则此时ΔA
1 A
2 A
3为正三角形。
证明:用反证法。设正定向ΔP1P2P3不是正三角形,且具有有向截长
。不妨设三个内角
,则由(1)式和(12)式可知
进而再由(12)式可得各内角相等,由(2)式可得各边长相等,与A
1 A
2 A
3不是正三角形的假设矛盾,故A
1 A
2 A
3只能是正三角形,结论得证。
至此,可将定理2和定理4合并写为下列结论。
定理5:对于奇数边数n 的情形,上述正定向n边形
若是凸的并且仅具有唯一的小于各边之长的有向截长r使得所确定的等截分点n边形
恰好为正n边形,则奇数边数只能是n = 5。
关于三角形时的非正三角形解的存在性的证明,以及相关性质的讨论,可归结为对于相关连续函数的取值分布的讨论。
方程式(6)的三个方程在(1)式约束下以ΔABC的三内角
为变元之时,是相互等价的,等价于以其较小的两个内角
为变元之时的形式。除了具有对应于正三角形的特解
之外,它还存在其它的解,这些解将对应于钝角三角形。事实上,具体可讨论闭区域上的二元函数的零值分布状况。由(6)式等价形式构造函数
即要考虑其零值的分布,特别是当
之时的分布。注意到有
由连续函数的性质可知:对于
存在
满足方程式(6),且此时
,从而对应于钝角三角形为解的情形;既得下列结论。
定理6:对于
,存在以
为三个内角的钝角ΔA
1 A
2 A
3,在其三个顶点出发的射线A
1 A
2、A
2 A
3、A
3 A
1上可以分别取到唯一一组点P1、P2、P3使得有向截长A1P
1 = A
2P
2 = A
3P3并使ΔP1P2P3成为正三角形。此时ΔA
1 A
2 A
3的钝角
具有值域
。
证明:注意到 连续,而且在由
、
、
所围成的闭区域有边值条件
连续,而且在由
、
、
所围成的闭区域有边值条件
故由闭区间上连续函数的零点定理可知,
,存在
使得
。于是,可知所论存在性成立,且此时
。再注意到引理2,可知截长与钝角对边的比值必是唯一的。进一步注意到对应
的取值范围充满
,得知钝角
具有值域
。证毕。
引理7:若ΔA
1 A
2 A
3是正三角形等截分逆问题的解,即在其三个顶点出发的射线A
1 A
2、A
2 A
3、A
3 A
1上可以分别取到点P1、P2、P3使得有向截长A1P
1 = A
2P
2 = A
3P3并使ΔP1P2P3成为正三角形,并且ΔA
1 A
2 A
3不是正三角形,则ΔA
1 A
2 A
3的三个内角两两不相等。
证明:按上文中的记号,注意到
,
,既得
。而
从而
,证毕。
定理8:若ΔA
1 A
2 A
3是正三角形等截分逆问题的解,并且ΔA
1 A
2 A
3不是正三角形,则ΔA
1 A
2 A
3只能是定理6之中所给定的一族钝角三角形。
证明:按上文中的记号,现由引理7不妨设
,则
,
,
。注意到引理4及其证明过程,得知
。而注意到(12)式即知

现若
,则再注意到(12)式即知
此时,由ΔA
1 A
2 A
3不是正三角形和定理3即知只能有
于是,相应截点P1落在边A
1 A
2上,同时截点P3落在边A
3 A
1的延长线上,从而对应角度之间具有关系
即得矛盾。因而只能有
此时依次得知
进而
此即对应为定理6之中所给定的钝角三角形,证毕。
对于一般的多边形边数大于等于4的情形,讨论所论逆问题解的分类问题是有意义的,但预期是复杂的,有待于进一步研究。
基金项目
本项研究受到国家自然科学基金资助,项目号11471039,11971057。